Continuité et Suites 2

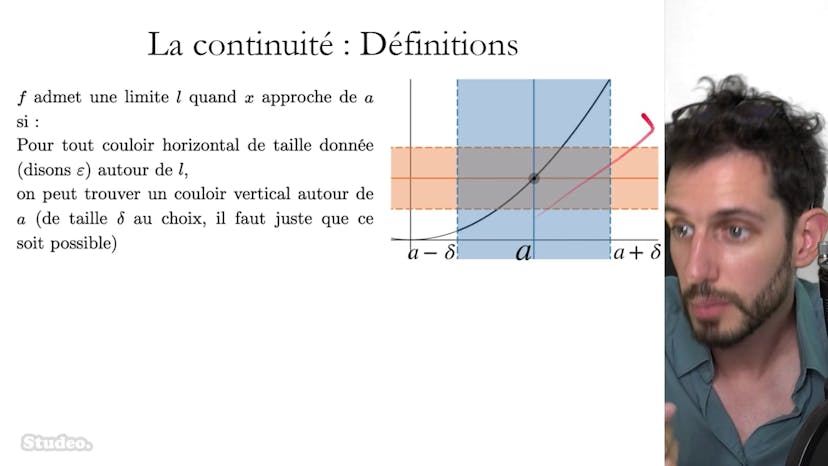
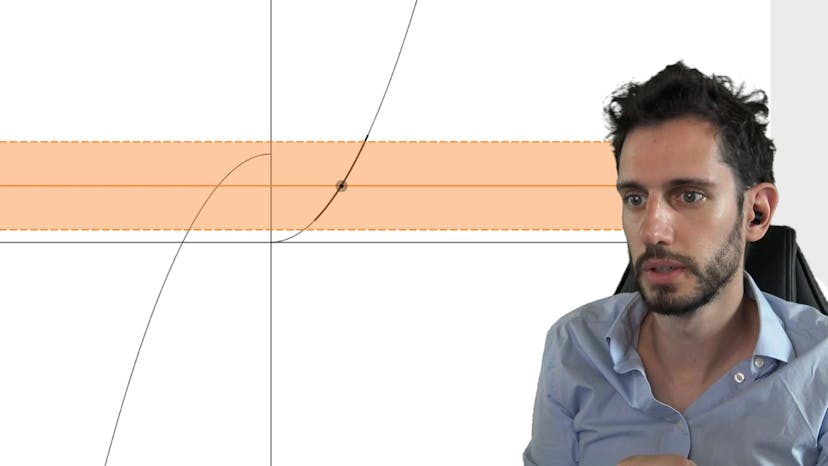
Dans ce cours, nous étudions les suites définies par récurrence et comment trouver leur limite. Tout d'abord, nous associons une fonction f à la suite et définissons la suite de manière à ce que u(n+1) = f(u(n)). Nous commençons par étudier la fonction f et sa continuité est essentielle. Ensuite, nous résolvons l'équation f(x) = x pour trouver les solutions possibles pour la limite de la suite. Ensuite, nous étudions la dérivabilité de la fonction f et utilisons la méthode de dérivation pour déterminer si elle est croissante. Il est important de noter que la fonction f peut ne pas être définie pour certains points, ce qui affecte sa croissance. Ensuite, nous démontrons par récurrence que la suite est strictement croissante et bornée. Cela nous permet de conclure que la suite converge vers une limite. En utilisant la continuité de f et les propriétés de la suite, nous pouvons déterminer la limite en trouvant la valeur qui satisfait f(x) = x. La continuité de f est cruciale car elle garantit que la limite recherchée est bien une solution. Une autre fonction f qui n'est pas continue envoie la suite vers une limite différente, ce qui souligne l'importance de la continuité pour appliquer le théorème. En conclusion, ce cours explique la méthode pour trouver la limite des suites définies par récurrence en utilisant la continuité de la fonction f et la propriété de récurrence.