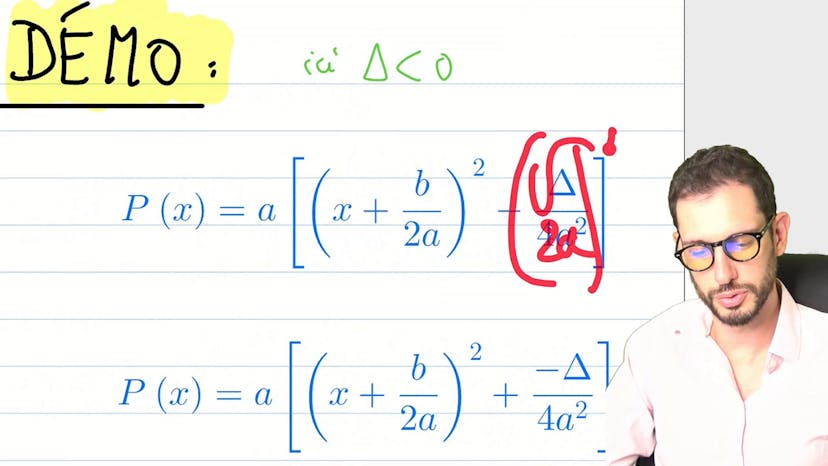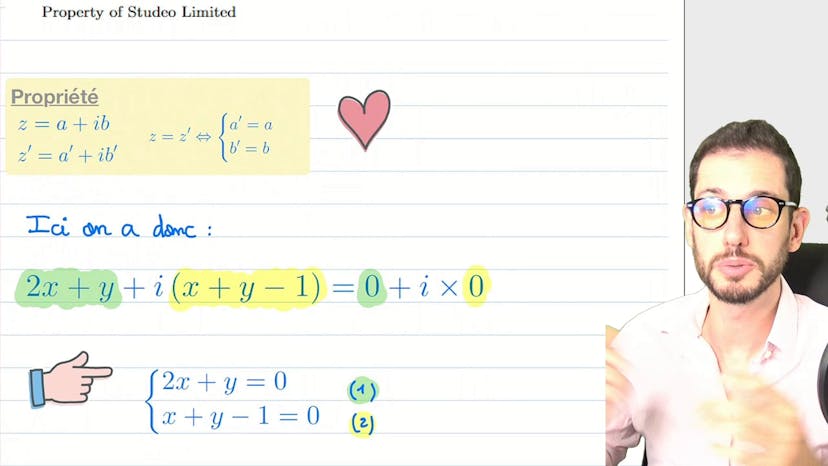
Binôme de Newton

Le cours parle de la formule du binôme de Newton, qui permet de calculer la puissance d'une somme de deux nombres (A + B)^N. Il explique que cette formule peut être utilisée pour tout nombre complexe A et B. Pour rappel, la formule est la suivante : A^N + (N parmi 1) * A^(N-1) * B + (N parmi 2) * A^(N-2) * B^2 + ... + B^N. Le professeur explique que la formule peut sembler compliquée, mais qu'en pratique, on peut la gérer de manière plus simple en suivant deux aspects. Le premier aspect est de se rendre compte qu'il y a N+1 termes dans la formule, du terme 1 au terme N, ainsi que le terme 0. Chaque terme correspond à une combinaison de puissances de A et B dont la somme est toujours égale à N. Par exemple, pour N=6, on aurait les termes A^6, A^5 * B, A^4 * B^2, A^3 * B^3, A^2 * B^4, A * B^5, B^6. Le deuxième aspect est la nature de chaque terme. Chacun d'entre eux est un produit de A et B avec des puissances cohérentes, et leur quantité peut être calculée à l'aide de factoriels ou du triangle de Pascal. Le triangle de Pascal permet de trouver les coefficients des différents termes pour chaque valeur de N, en suivant les règles suivantes : il y a toujours un 1 au début et à la fin de chaque ligne, et chaque coefficient est la somme des deux coefficients au-dessus de lui dans le triangle. Le professeur donne des exemples concrets pour illustrer l'utilisation de la formule, et explique que le but est de pouvoir comprendre et appliquer la logique du triangle de Pascal et du binôme de Newton, plutôt que de mémoriser la formule brute. Enfin, il donne un exemple spécifique en utilisant la formule pour calculer la puissance de (3-2i)^5, en rappelant une propriété intéressante sur les puissances successives de i. Il invite les étudiants à faire le calcul eux-mêmes et à poser des questions s'ils en ont besoin.