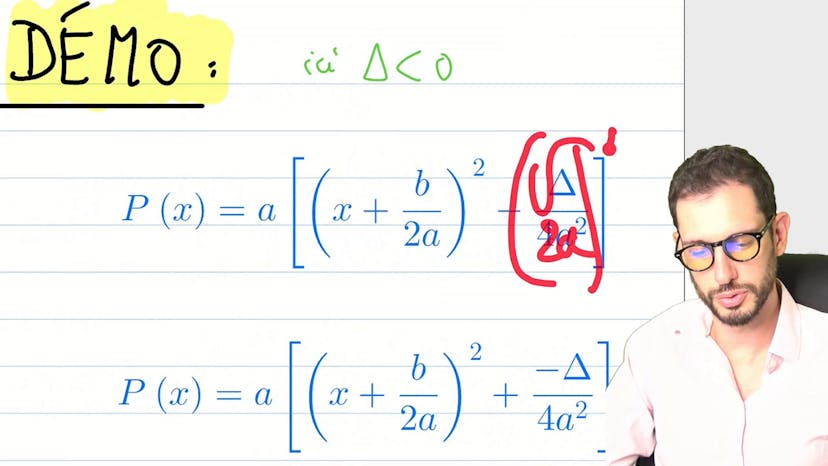Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Arithmétique
- Complexes
- Probabilités
- Structures algébriques
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Arithmétique
- Complexes
- Probabilités
- Structures algébriques
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Z est-il réel ? V1
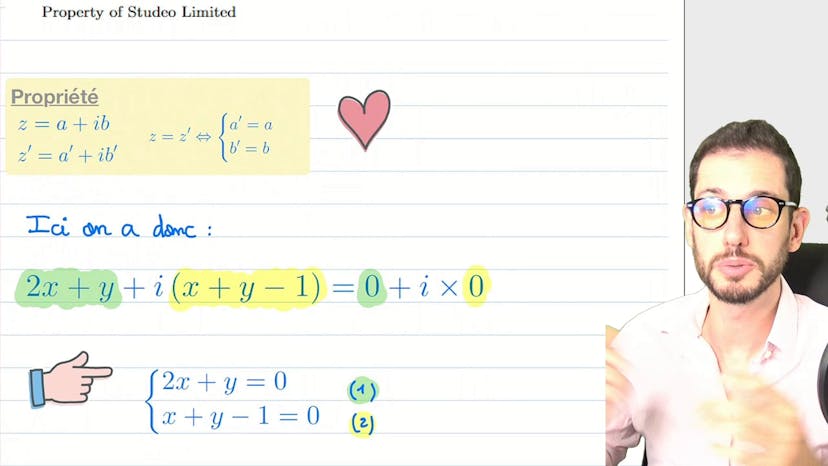
Ce cours aborde une méthode classique en mathématiques qui est souvent utilisée dans des exercices plus complexes. La méthode consiste à trouver l'ensemble de valeurs d'un complexe "z" pour lesquelles une quantité donnée, appelée "grand z", est réelle. On utilise la méthode de la quantité conjuguée pour simplifier l'expression et obtenir une conclusion. Dans cet exercice, on nous donne un petit z qui n'est pas égal à moins 1 et on nous demande de trouver les valeurs de ce petit z pour lesquelles grand z est réel. En utilisant la méthode de la quantité conjuguée, on développe l'expression et sépare les termes réels. On simplifie ensuite l'expression et on trouve que b doit être nul pour que le petit z soit réel. La solution finale est donc l'ensemble des nombres réels à l'exception de moins 1.