Z est-il réel ? V2

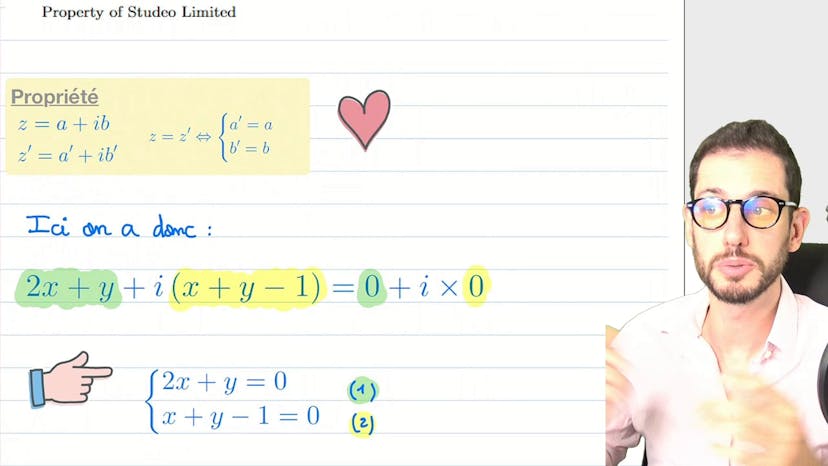
Le cours présente une méthode pour déterminer si un nombre complexe est réel en utilisant la propriété du conjugué. Le conjugué d'un nombre complexe est obtenu en changeant le signe de sa partie imaginaire. Si un nombre complexe est égal à son conjugué, alors il est réel. Cette méthode est élégante mais pas toujours optimale, car certains cas nécessitent l'utilisation des coefficients A et B. Le cours explique comment appliquer la propriété du conjugué dans différentes opérations mathématiques, telles que la soustraction et la multiplication, pour simplifier les expressions. En appliquant ces propriétés, on arrive à la conclusion que si un nombre complexe est égal à son conjugué, alors il est réel. Cette méthode est présentée comme une astuce supplémentaire à connaître, mais il est recommandé de comprendre le concept du conjugué pour l'utiliser correctement.