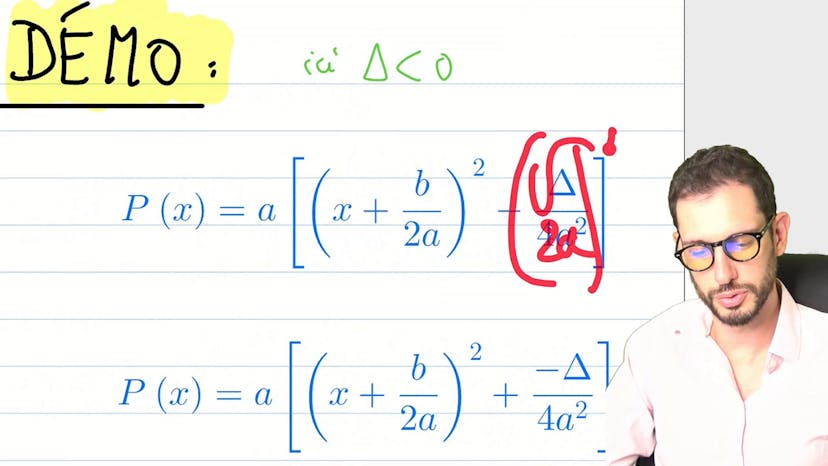Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Arithmétique
- Complexes
- Probabilités
- Structures algébriques
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Arithmétique
- Complexes
- Probabilités
- Structures algébriques
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
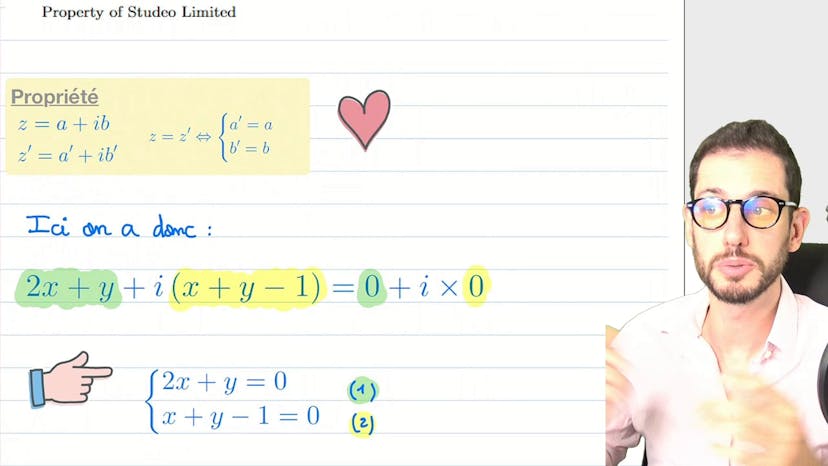
Inégalité triangulaire, partie réelle et imaginaire d’un quotient
Dans ce cours, Paul aborde plusieurs questions sur les complexes. Pour la première question, il utilise l'inégalité triangulaire pour établir une inégalité. Pour la deuxième question, il explique comment exprimer la partie réelle et la partie imaginaire de A sur B en fonction des parties réelles et imaginaires de A et B, ainsi que du module de B. Paul suggère d'utiliser les formules qui lient partie réelle, partie imaginaire, module, et le nombre et son conjugué. Ensuite, il calcule les parties réelles et imaginaires de 1+Eialpha et 1+Eibêta. Il fait également référence à la formule de l'air pour simplifier les calculs. Il note que cette formule est très utile dans les problèmes complexes et encourage à la retenir. En conclusion, Paul résume les résultats obtenus et donne quelques conseils pour mieux visualiser les angles complexes. Il termine en soulignant l'importance de comprendre les formules de l'air.