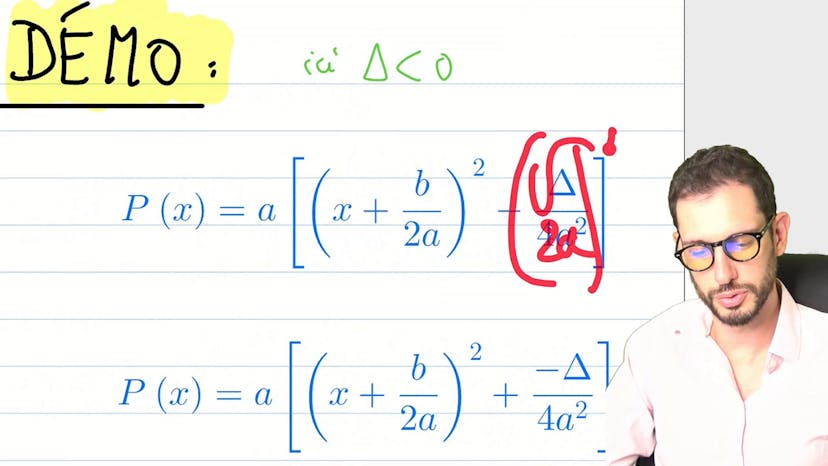Équations polynomiales

Dans cette vidéo, Paul explique comment résoudre des équations du second degré à coefficient complexe. La technique pour résoudre ces équations est similaire à celle des équations en réel. Les solutions de l'équation AZ² + BZ + C = 0 sont Z1 = (-B - √Δ)/2A et Z2 = (-B + √Δ)/2A, où Δ = B² - 4AC. Paul résout une première équation avec A = 1, B = 1 et C = 1, et obtient les solutions Z1 = 1 + i et Z2 = 1 + 2i. 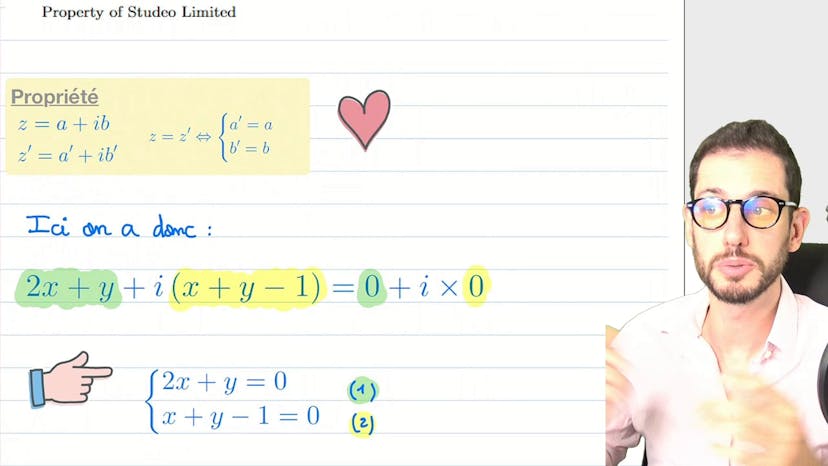Ensuite, Paul aborde une deuxième équation déguisée en équation du second degré en utilisant la substitution X = Z3. Il résout l'équation du second degré en X et trouve Δ = -15 - 8i. Pour trouver la racine carrée de Δ, il pose Δ = a + ib et utilise l'équation Δ² = Δ, ce qui donne les équations sur la partie réelle et la partie imaginaire de Δ. En résolvant ces équations, il obtient A = 1 et B = -4, ou A = -1 et B = 4. Les solutions de cette deuxième équation sont x1 = 1 - i et x2 = 3i. Cependant, Paul souhaite maintenant trouver les solutions pour l'équation originale. Il résout l'équation E1 en écrivant Z3 = 1 - i ou Z3 = 3i, sous forme exponentielle. Il utilise la racine 1ère de l'unité pour résoudre cette équation et obtient six solutions au total. Il conclut en disant que cela est cohérent avec le fait que le polynôme de départ était de degré 6. Ce résumé explique comment résoudre des équations du second degré à coefficient complexe et décrit les étapes suivies par Paul pour résoudre deux exemples spécifiques.