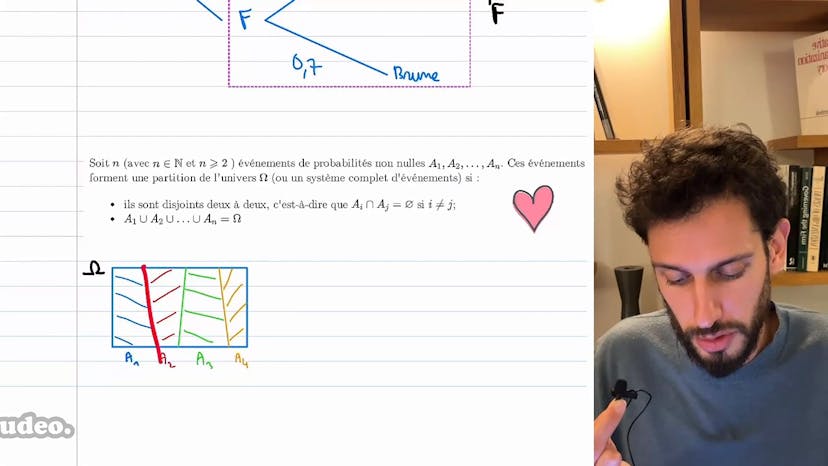
Les probabilités conditionnelles

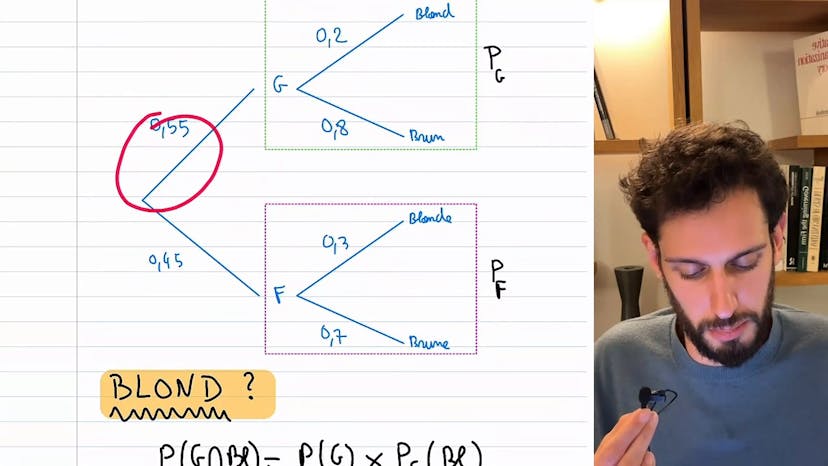
Lors de l'introduction des probabilités, il est souvent plus facile de commencer par un exemple concret plutôt que des formules théoriques. Dans cet exemple, nous considérerons un lycée où il y a 55% de garçons et 45% de filles. Parmi les garçons, 20% sont blonds et 80% sont bruns. Parmi les filles, 30% sont blondes et 70% sont brunes. Nous pouvons définir les probabilités conditionnelles, qui sont les probabilités dans un sous-univers. Par exemple, la probabilité d'être blond est de 20% pour les garçons et de 30% pour les filles. Chaque probabilité conditionnelle est définie en fonction du sous-univers dans lequel nous nous trouvons. Nous pouvons également calculer la probabilité d'un événement donné en combinant différentes probabilités conditionnelles. Par exemple, la probabilité d'être un garçon blond est de 0,55 (probabilité d'être un garçon) multipliée par 0,2 (probabilité d'être blond parmi les garçons). De même, la probabilité d'être une fille blonde est de 0,45 (probabilité d'être une fille) multipliée par 0,3 (probabilité d'être blond parmi les filles). Nous pouvons aussi exprimer la probabilité d'un événement dans un sous-univers en utilisant la probabilité totale et la probabilité de l'événement dans cet univers. Par exemple, la probabilité d'être blonde parmi les filles est la probabilité d'être une fille blonde divisée par la probabilité d'être une fille. La formule générale pour les probabilités conditionnelles est la probabilité de l'événement B sachant l'événement A, divisée par la probabilité de l'événement A. Cette formule peut être appliquée à n'importe quel événement A et B.