La formule des probas totales

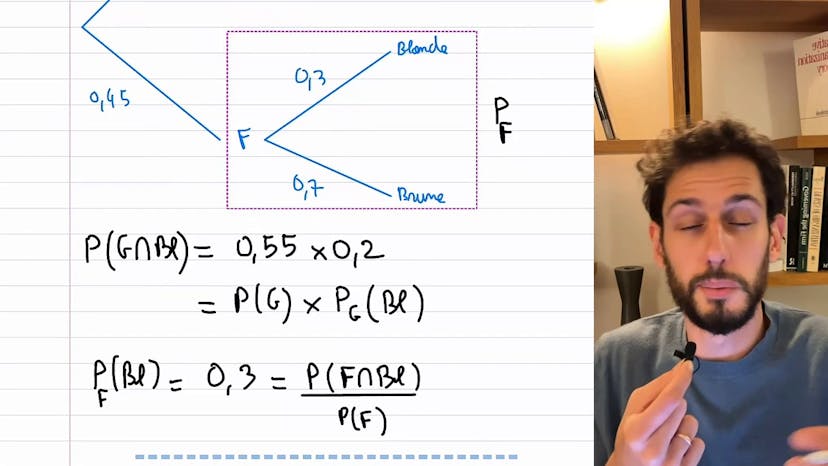
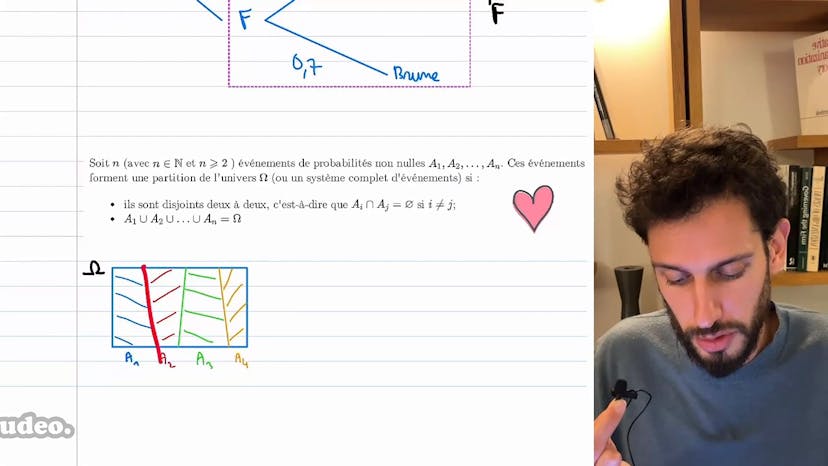
La formule des probabilités totales est une formule très importante que l'on peut appliquer pour calculer des probabilités dans un contexte donné. Dans cet exemple, nous prenons le lycée comme univers et nous créons une partition entre garçons et filles, ainsi qu'entre les différentes couleurs de cheveux. Nous avons utilisé la formule des probabilités conditionnelles pour calculer la probabilité d'être à la fois blond et garçon, en multipliant la probabilité d'être garçon par la probabilité d'être blond parmi les garçons. Maintenant, nous pouvons nous intéresser à une probabilité plus globale, celle d'avoir les cheveux blonds. Imaginons un lycée avec 100 personnes, 55 garçons et 45 filles. Nous voulons savoir quelle est la probabilité, en tirant une personne au hasard, de tomber sur quelqu'un qui a les cheveux blonds, qu'il soit garçon ou fille. L'idée est de ne pas se focaliser uniquement sur les personnes blondes, mais de prendre en compte les deux catégories. Il y a deux chemins possibles pour tirer une personne blonde : soit on tire un garçon blond, soit on tire une fille blonde. La formule des probabilités totales consiste à sommer les probabilités de ces deux événements pour obtenir la probabilité d'être blond. En d'autres termes, la probabilité d'être blond est égale à la probabilité d'être un garçon blond plus la probabilité d'être une fille blonde. On peut aussi écrire cela en utilisant la formule des probabilités conditionnelles. Cette formule nous permet de parcourir toutes les branches de l'arbre des événements et de les sommer pour obtenir la probabilité recherchée. En théorie, si nous avons une partition de l'univers, la probabilité d'un événement B est égale à la somme des probabilités de B dans chaque branche de la partition. Cette formule peut être utilisée en remplaçant chaque probabilité par la formule des probabilités conditionnelles correspondante. Il est important de comprendre intuitivement le sens de cette formule : nous cherchons l'événement dans chaque branche et les sommons toutes. J'espère que cela était clair. N'hésitez pas à laisser des commentaires si nécessaire. À bientôt dans une prochaine vidéo !