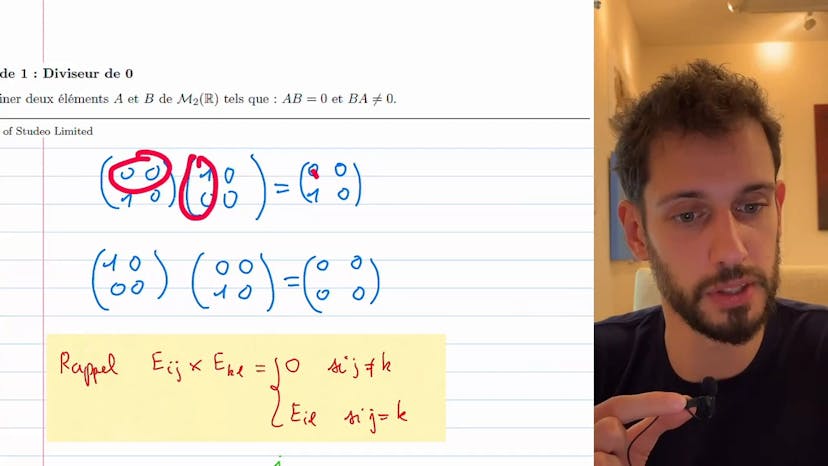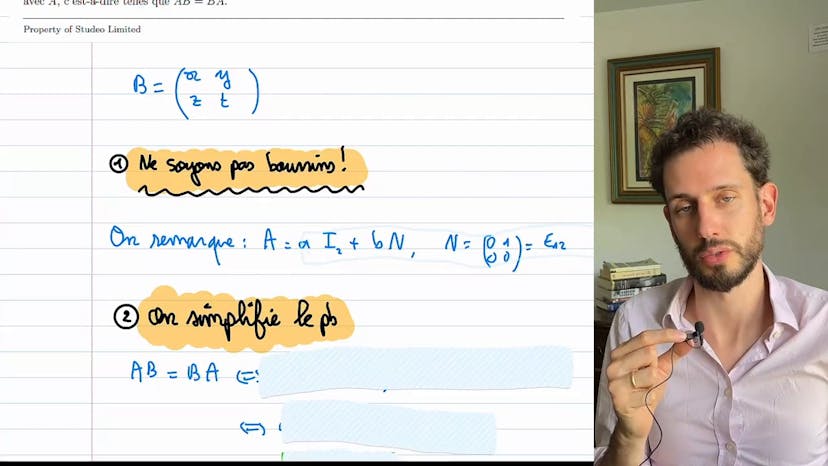Centre de Mn

Le cours porte sur la détermination du centre de la matrice Mn2R, qui est l'ensemble des matrices A dans Mn2R telles que A*M = M*A pour toutes les matrices M de Mn2R. Il est tout d'abord mentionné que la matrice identité IN appartient au centre, ainsi que lambda*IN. En d'autres termes, toutes les matrices diagonales avec des coefficients sur la diagonale égales à lambda font partie du centre. Ensuite, le cours explique qu'il faut trouver des conditions sur les coefficients de la matrice A pour qu'elle puisse commuter avec toutes les autres matrices de Mn2R. Pour cela, on peut choisir les matrices EIG de la base canonique de l'espace des matrices, où chaque matrice EIG a des zéros partout sauf un 1 croisant la ligne I et la colonne J. En multipliant A par EIG et en calculant A*M et M*A, on peut déterminer les conditions sur les coefficients de la matrice A. On obtient ainsi que les seules matrices qui commutent avec toutes les autres sont les lambda*IN, c'est-à-dire les matrices diagonales avec des coefficients sur la diagonale égales à lambda. En résumé, le centre de Mn2R est constitué uniquement des matrices diagonales avec des coefficients sur la diagonale égales à lambda.