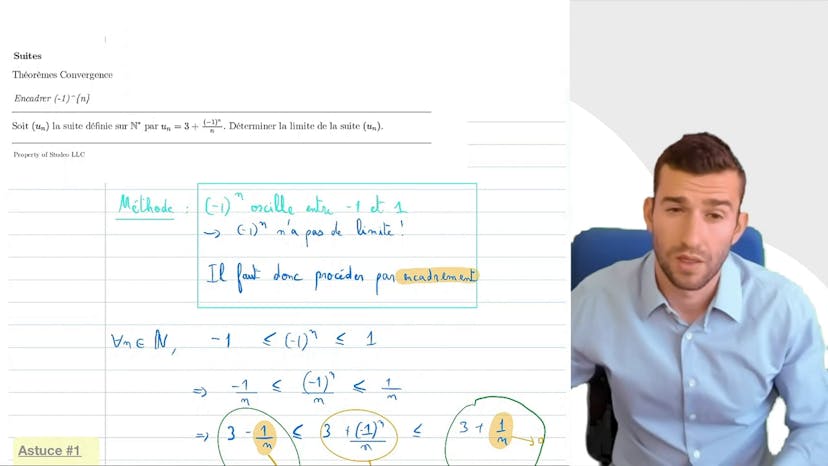Encadrer sin(n)

Dans cette vidéo, nous allons étudier deux exemples de suites en utilisant les théorèmes de convergence. Le premier exemple concerne la suite u_n = n + 2 * sin(n). Nous devons montrer que pour tout entier n, u_n est supérieur à n - 2. Pour encadrer la fonction sinus, nous savons que le sinus est toujours compris entre -1 et 1. En multipliant par 2, nous obtenons une valeur positive. En ajoutant n, nous obtenons finalement que u_n est supérieur à n - 2. Bien que cette partie de l'inéquation ne soit pas importante, elle est vraie. Ce qui nous intéresse vraiment est le fait que u_n est supérieur à n - 2. Comme n - 2 tend vers plus l'infini, et que u_n est plus grand qu'une suite telle que n - 2, nous pouvons conclure que u_n tend vers l'infini. Le deuxième exemple concerne la suite v_n = -n^2 + (-1)^n. Encore une fois, nous devons encadrer la puissance (-1)^n, qui est toujours entre -1 et 1. Le terme (-1)^n n'aura pas beaucoup d'importance, car il va alterner entre -1 et 1. Le terme dominant est n^2, qui tend vers moins l'infini. En encadrant la suite, nous obtenons que v_n est inférieur à une suite qui tend vers moins l'infini. En factorisant le terme dominant, nous obtenons v_n = n^2 * (-(1/n) + 1/n^2). La partie à droite tend vers 1, et la partie à gauche tend vers moins 1. Donc v_n tend vers moins l'infini. En utilisant l'encadrement, nous avons montré que les deux suites étudiées tendent toutes les deux vers l'infini et moins l'infini, respectivement.