Convexité et Inégalités

Dans ce cours, nous étudions la méthode de la convexité en SEO friendly. La méthode est assez classique et facile à appliquer une fois que l'on maîtrise l'étude de la convexité. Nous commençons par nous intéresser à une fonction f(x) égale à x^3 - 2x^2, qui est un polynôme dérivable deux fois. Nous calculons les deux dérivées de cette fonction : f'(x) = 3x^2 - 4x et f''(x) = 6x - 4. Nous souhaitons étudier le signe de f''(x) pour déterminer la concavité et la convexité de la fonction. En résolvant l'inéquation 6x - 4 > 0, nous trouvons que x > 3/2. En résolvant l'inéquation 6x - 4 < 0, nous trouvons que x < 3/2. Nous en déduisons que la fonction f est concave sur l'intervalle ]-∞, 3/2] et convexe sur l'intervalle [3/2, +∞]. Ensuite, on nous demande l'équation de la tangente de f au point -1. En utilisant la formule y = f'(1)(x - (-1)) + f(1), nous trouvons que l'équation de la tangente est y = 7x + 4. 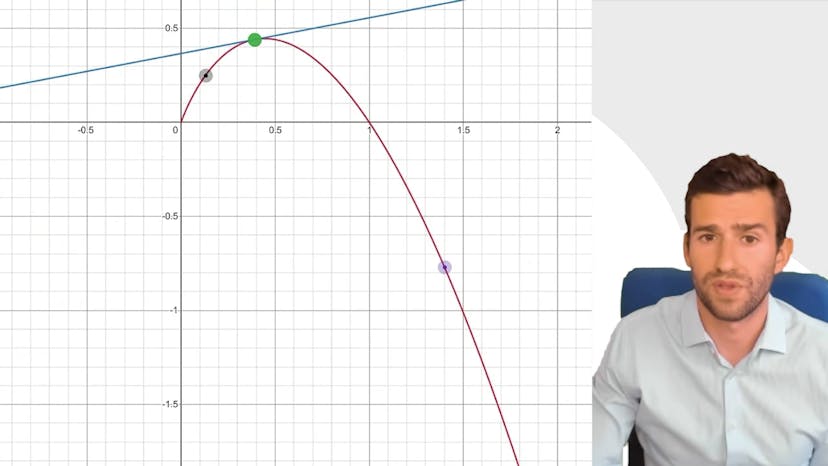Nous devons ensuite déduire que pour tout x négatif, x^3 - 2x^2 < 7x + 4. En analysant cette inégalité, nous observons que 7x + 4 est l'équation de la tangente que nous avons calculée précédemment, et x^3 - 2x^2 est la fonction f. Ainsi, géométriquement, cette inégalité signifie que la courbe représentant la fonction f est située en dessous de sa tangente. Cela est vrai lorsque la fonction est concave, ce qui est le cas sur l'intervalle ]-∞, 3/2]. Par conséquent, nous avons bien l'inégalité souhaitée. Il est important de noter que cette méthode repose sur l'analyse de la convexité de la fonction. Sans cette notion, on ne pourrait pas résoudre l'équation x^3 - 2x^2 < 7x + 4, car elle implique un polynôme de degré 3. Il faut donc toujours penser à la convexité pour résoudre ce type d'équations. En conclusion, la méthode de la convexité nous permet d'étudier la concavité et la convexité d'une fonction, de trouver l'équation de la tangente en un point et d'établir des inégalités entre une fonction et sa tangente. N'hésitez pas à consulter la FAQ si vous avez des questions supplémentaires.