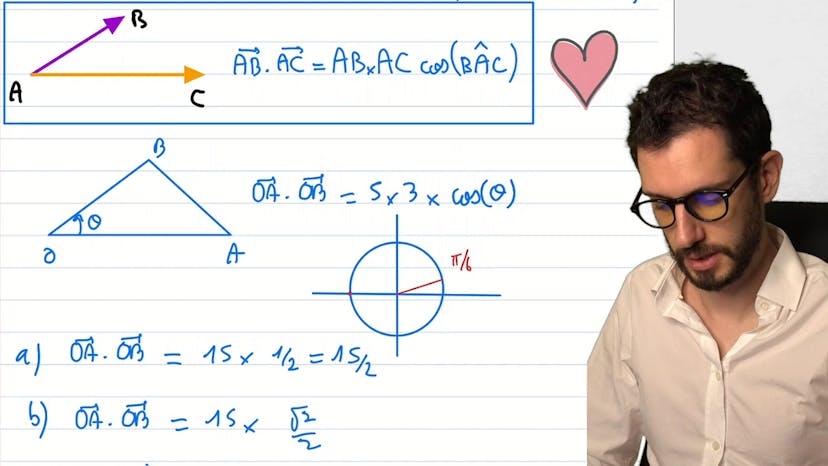Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Produit Scalaire
- Géométrie avec Repères
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Produit Scalaire
- Géométrie avec Repères
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Définition de base : avec projeté
Le cours traite des propriétés fondamentales du produit scalaire. Le produit scalaire est défini comme le produit de deux vecteurs, qui est égal à la norme des vecteurs s'ils sont dans le même sens et moins le produit des deux normes s'ils sont dans des sens opposés. Si les vecteurs ne sont pas alignés, le produit scalaire sera égal à la version projetée du vecteur sur l'autre. Le cours utilise l'exemple d'un losange pour illustrer ces concepts et calcule plusieurs produits scalaires en utilisant la projection. Il rappelle également que le produit scalaire de deux vecteurs est nul s'ils sont orthogonaux. Enfin, le cours insiste sur l'utilité de la projection pour calculer des produits scalaires plus facilement.