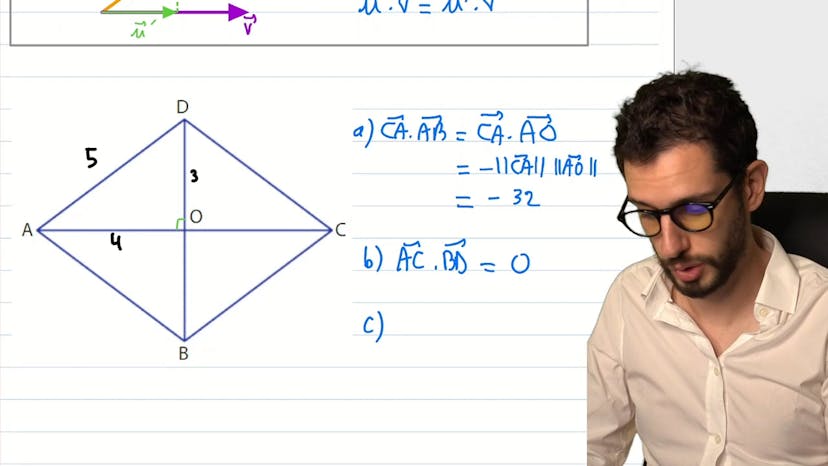
Définition avec le cosinus

La méthode enseignée est une manière d'utiliser la formule classique du produit scalaire AB scalaire AB qui est le produit des normes fois le cosinus de l'angle qui sépare les deux vecteurs. Pour l'appliquer, on prend l'exemple d'un triangle OAB avec OA=5 et OB=3, et on calcule le produit scalaire OA scalaire OB pour différentes valeurs de l'angle theta, soit pi sur 3, pi sur 4, et 5pi sur 6. Pour calculer le cosinus de theta, on utilise des rappels de trigonométrie. Pour le cas de 5pi sur 6, il est expliqué que le produit scalaire peut être négatif à cause de l'angle obtus du triangle. Cette méthode est présentée comme une manière d'illustrer le cours, plutôt qu'une résolution de problème.