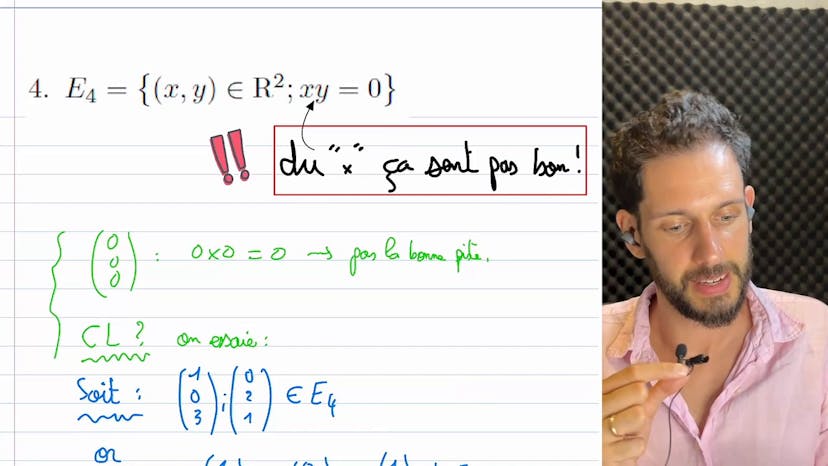Combinasion Linéaire

Dans cette vidéo, il est expliqué l'importance des combinaisons linéaires dans le domaine des espaces vectoriels. Différents exemples sont donnés où l'on demande si un vecteur peut être exprimé comme une combinaison linéaire d'autres vecteurs. Pour résoudre cela, on utilise des coefficients de combinaisons linéaires et on vérifie s'il existe une solution au système correspondant. On explique également qu'il est parfois plus simple de résoudre mentalement certains cas, mais dans d'autres cas, il est nécessaire de faire les calculs de manière plus détaillée. Un petit bonus est mentionné sur l'utilisation de deux vecteurs non parallèles comme base dans un plan. Dans le premier exemple, on démontre que le vecteur (1,2) peut être exprimé comme une combinaison linéaire des vecteurs u1 et u2. Dans le deuxième exemple, on démontre que le vecteur (-1/7,4/7) peut également être exprimé comme une combinaison linéaire des vecteurs u1, u2 et u3. Dans le troisième exemple, on résout un système de trois équations pour trouver les valeurs des coefficients de combinaisons linéaires, et on montre que le vecteur (2,4) ne peut pas être exprimé comme une combinaison linéaire des deux premiers vecteurs. Dans le quatrième exemple, on montre que la possibilité d'exprimer le vecteur (2,4) comme une combinaison linéaire des deux premiers vecteurs dépend de la valeur de m. On conclut en soulignant l'importance de savoir utiliser les combinaisons linéaires et en encourageant les questions des spectateurs.