 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Divisibilité et division euclidienne
- Congruences
- PGCD et algorithme d’Euclide
- Nombres premiers
- Prépare tes écrits
- Loi usuelles, groupes
- Anneaux corps
- 11- Prépare tes écrits
- Opérations sur les matrices
- Puissance de matrices
- Systèmes linéaires et Inverses de matrices
- 12- Prépare tes écrits
- Espaces vectoriels et sous-espaces vectoriels
- Famille de vecteurs
- Somme d'espaces vectoriels
- Matrices applications linéaires
- Changement de base, matrices de passages
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Divisibilité et division euclidienne
- Congruences
- PGCD et algorithme d’Euclide
- Nombres premiers
- Prépare tes écrits
- Loi usuelles, groupes
- Anneaux corps
- 11- Prépare tes écrits
- Opérations sur les matrices
- Puissance de matrices
- Systèmes linéaires et Inverses de matrices
- 12- Prépare tes écrits
- Espaces vectoriels et sous-espaces vectoriels
- Famille de vecteurs
- Somme d'espaces vectoriels
- Matrices applications linéaires
- Changement de base, matrices de passages
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Algèbre
MPSI/PCSI
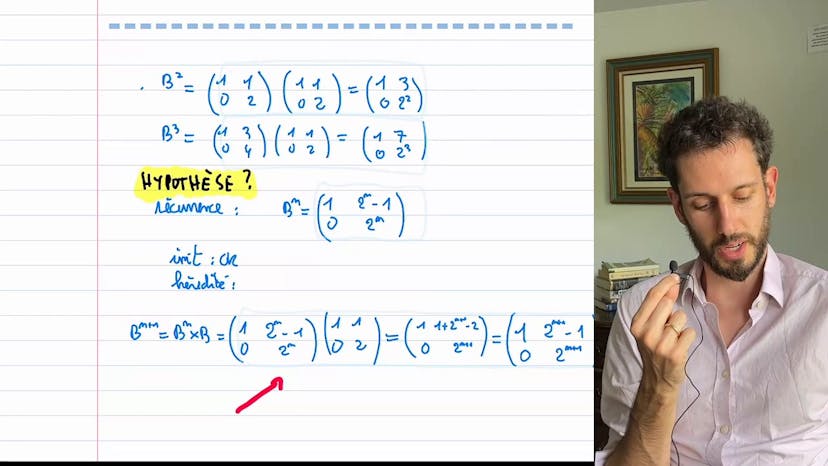
Puissance nième réccurence
Le cours porte sur le calcul de puissances de matrices et l'importance de trouver l'intuition rapidement. L'exemple donné est de calculer A puissance N et B puissance N. Il est recommandé de commencer par calculer les petites puissances pour avoir une idée du résultat. En utilisant la récurrence, on peut déduire que A puissance N est égal à 2 puissance N moins 1 fois A. Pour B, on fait également le même processus et on remarque que le coefficient est proche de 2 puissance N moins 1. On initie le calcul avec B puissance N plus 1 égal B puissance N fois B et cela fonctionne. Il est possible d'essayer différentes hypothèses jusqu'à ce que la récurrence fonctionne. En conclusion, il est important de trouver l'intuition rapidement et de faire des essais par à-coups pour résoudre des problèmes mathématiques.
Maths
Algèbre
MPSI/PCSI

Puissance nième binome Newton
Ce cours traite de la matrice N, une matrice nilpotente qui finit par s'annuler quand on la monte en puissance. Cette matrice est très importante et intervient dans de nombreux exercices en mathématiques. En la montant en puissance, la diagonale de 1 se déplace jusqu'à disparaître complètement. Cette propriété est valable pour toute dimension de la matrice N. On peut utiliser cette matrice dans des calculs en utilisant le binôme de Newton, en sachant que les termes où B a une puissance supérieure à 3 sont nuls. On peut exprimer cette formule sous forme matricielle en remplaçant les puissances par des matrices N. En résumé, il est important de connaître cette matrice nilpotente dans le domaine des mathématiques.
Maths
Algèbre
MPSI/PCSI
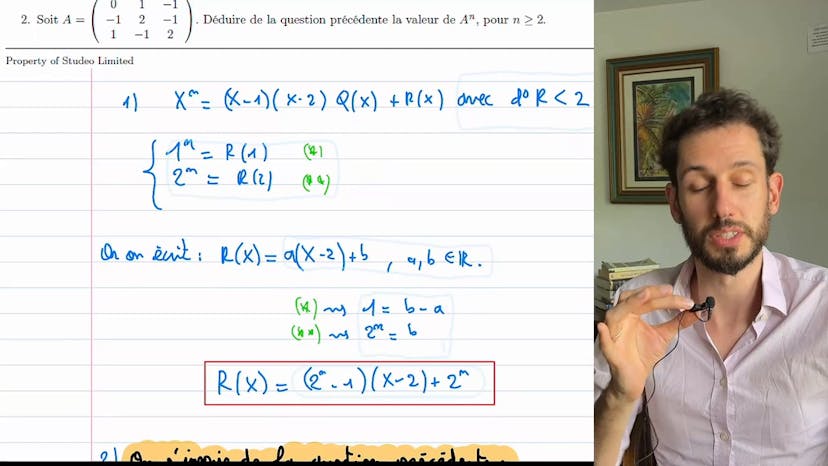
Puissance nième Polynome annulateur
Dans ce cours, on étudie la division euclidienne du polynôme x^n par le polynôme x^2 - 3x + 2. Pour calculer le polynôme reste R2x, on utilise les racines x=1 et x=2 du polynôme diviseur pour éliminer le terme Q2x dans l'équation. On obtient ainsi le polynôme reste R2x qui est de degré 1 et peut s'écrire sous la forme AX + B. En résolvant les équations, on trouve que B=2^n et A=2^n-1. Le polynôme reste R2x peut donc s'écrire comme 2^n-1 * (x-2) + 2^n.
Ensuite, on applique cette structure polynomiale à une matrice A. En remarquant que A^2 - 3A + 2I = 0, on déduit que A^n = R2A. Ainsi, on peut calculer A^n en utilisant le polynôme reste R2A qui s'écrit comme 2^n-1 * (A-2I) + 2^n * I.
Maths
Algèbre
MPSI/PCSI

Matrices nilpotentes
Dans cet exercice, nous étudions les propriétés des matrices nilpotentes. Une matrice nilpotente est une matrice pour laquelle il existe une puissance à partir de laquelle toutes les puissances de la matrice sont nulles. Par exemple, si a² est différent de zéro, a³ est différent de zéro, mais a⁴ est égal à zéro, alors toutes les puissances de a à partir de a⁴ seront également nulles. Nous devons démontrer que si deux matrices nilpotentes, a et b, commutent, alors a + b est également nilpotente.
Nous traduisons cela en termes mathématiques en disant qu'il existe un entier p tel que a^p = 0 et un entier q tel que b^q = 0. De plus, nous avons a * b = b * a, car les matrices commutent. Notre objectif est de montrer que pour tout entier m, il existe un entier n tel que (a * b)^m = 0 et (a + b)^n = 0.
Pour prouver cela, nous utilisons les propriétés des matrices commutantes. Par exemple, si les matrices commutent, alors (a * b)^m = a^m * b^m. Étant donné que a^p = 0 et b^q = 0, nous pouvons dire que (a * b)^p * q = a^p * b^q = 0. Donc, nous avons montré que le produit de deux matrices commutantes est également nilpotent.
De même, nous utilisons la formule du binôme pour montrer que (a + b)^n = a^n + n * (a^(n-1)) * b + ... + b^n. En choisissant n = p + q (la somme des indices de nilpotence), nous pouvons séparer les termes en a et b. Comme a^p = 0 et b^q = 0, tous les termes contenant des puissances plus élevées de a et b seront également nuls. Ainsi, nous avons prouvé que la somme de deux matrices commutantes est également nilpotente.
En conclusion, en utilisant les propriétés des matrices commutantes et la formule du binôme, nous avons démontré que si a et b sont deux matrices nilpotentes qui commutent, alors a + b est également nilpotente. Cette démonstration nécessite de comprendre la commutativité et d'appliquer les propriétés des matrices nilpotentes et des puissances de matrices.
Maths Approfondies
Algèbre
ECG
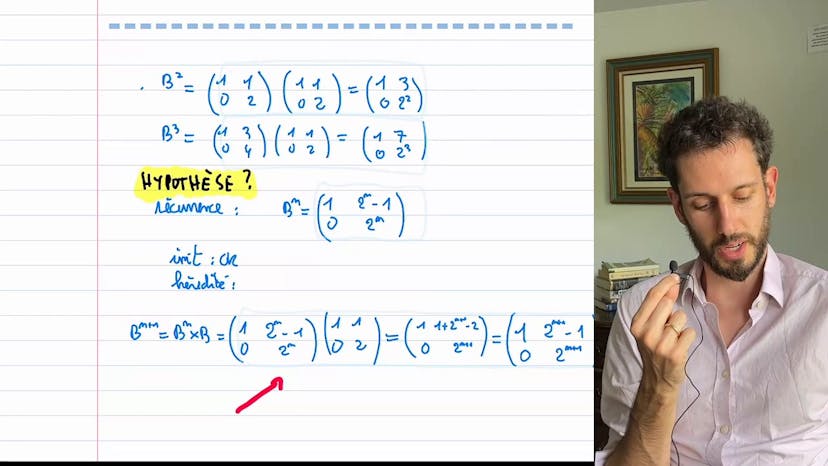
Puissance nième réccurence
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG

Puissance nième binome Newton
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG

Puissance nième Polynome annulateur
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG

Matrices nilpotentes
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Algèbre
ECG
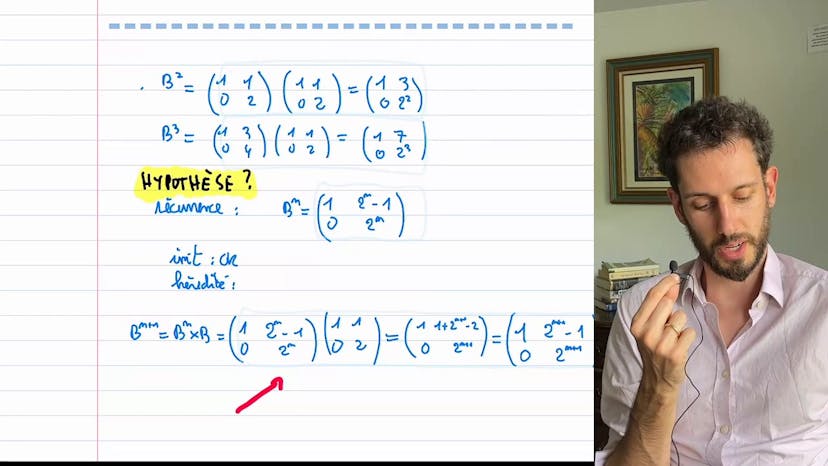
Puissance nième réccurence
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Algèbre
ECG

Puissance nième binome Newton
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Algèbre
ECG

Puissance nième Polynome annulateur
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Algèbre
ECG

Matrices nilpotentes
Aucun résumé n'est disponible pour cette vidéo


