Cours de Calcul matriciel et systèmes en Ligne par les Meilleurs Professeurs - Calcul matriciel et systèmes

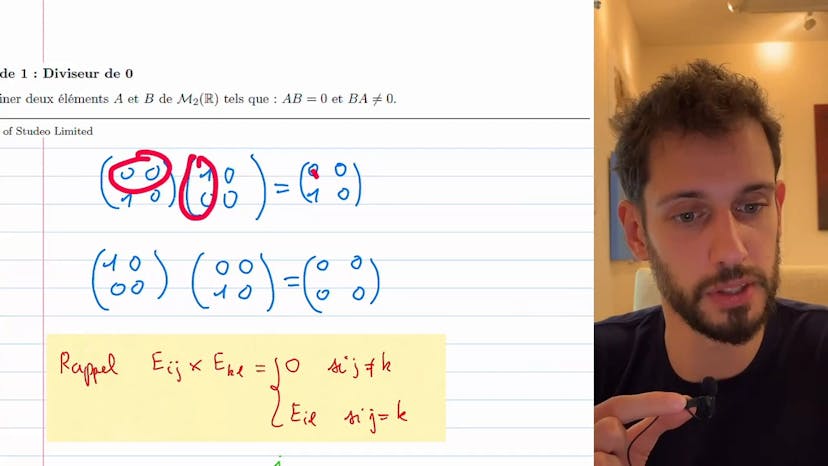
Diviseur de 0

Dans ce chapitre, nous abordons une méthode simple pour trouver des matrices et comprendre leur comportement. Nous devons trouver deux matrices de taille 2 dont le produit est égal à 0 dans un sens, mais pas dans l'autre sens. Cela souligne le fait que les matrices ne commutent pas nécessairement. Lorsque nous recherchons des exemples de matrices, le plus simple est de commencer par des matrices fondamentales, qui sont des matrices avec des zéros partout sauf à un endroit. Nous les appelons Eij, où i représente la ligne et j la colonne. A cet endroit, nous plaçons un 1. Une propriété intéressante de ces matrices est que le produit de Eij fois Ekl est toujours égal à 0, sauf lorsque la colonne de la première matrice rencontre la ligne de la deuxième matrice. Dans ce cas, nous avons une sorte de "choc" où Eijkl devient Eil lorsque j est égal à k. Si nous prenons l'exemple des matrices de base M22R, nous pouvons voir que le produit de Eij fois Ekl est égal à Ekl. En revanche, le produit de Ekl fois Eij est égal à 0 car les 1 ne se rencontrent jamais. Ainsi, cet exemple souligne l'importance d'utiliser des matrices simples avec beaucoup de zéros plutôt que de se compliquer la tâche. À la prochaine leçon !

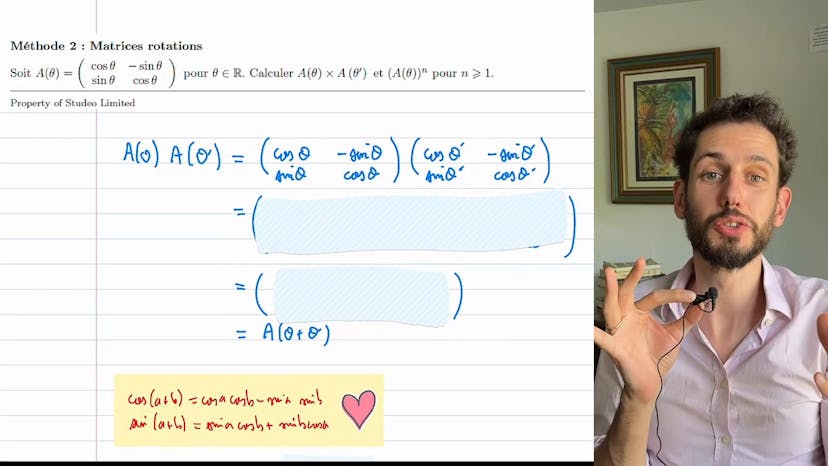
Matrices rotations

Dans cette vidéo, le cours porte sur le calcul avec des matrices, plus précisément sur une matrice appelée une matrice de rotation. Cette matrice relie les coordonnées cartésiennes aux coordonnées polaires en physique. L'objectif est de calculer Aθ fois Aθ' et ensuite Aθ'. On remarque que lorsqu'on effectue une rotation de 30° puis de 50°, on obtient une rotation totale de 80°. On espère donc que le produit de rotation a une forme simple en fonction de θ et θ'. Pour démontrer cela, on utilise une formule qui permet de reconnaitre certaines valeurs trigonométriques. En effectuant les remplacements nécessaires, on obtient A de θ plus θ'. Ensuite, on souhaite obtenir A de θ puissance n. En utilisant à nouveau la formule avec A de θ plus θ, on obtient A de θ². Par récurrence, on peut alors écrire que A de θ puissance n est égal à A de nθ. Il est important de bien comprendre ces concepts et d'effectuer les étapes de récurrence rapidement. Si vous avez des questions, n'hésitez pas à les poser. Au revoir et à bientôt pour une prochaine méthode.

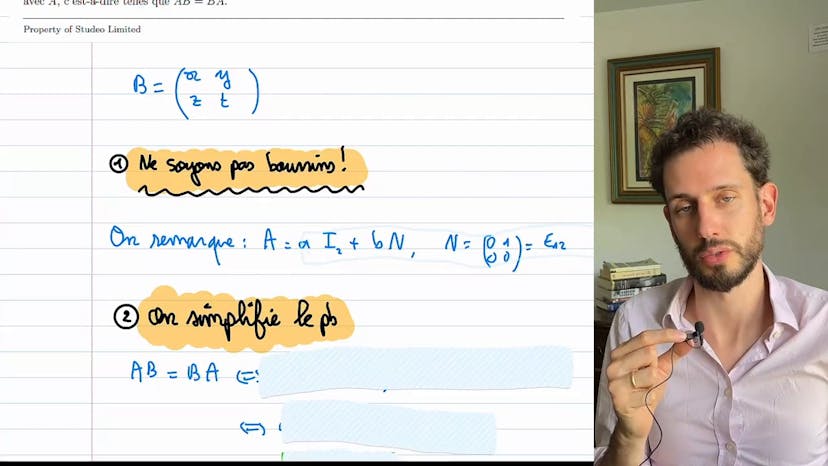
Commutant

Dans cet exercice, nous cherchons à trouver l'ensemble des matrices B qui commutent avec une matrice A donnée. Pour cela, nous observons que la matrice A peut être écrite comme la somme de deux matrices : A fois I2 (matrice identité) et B fois une matrice N (matrice triangulaire supérieure avec des 1 sur la diagonale). Cette matrice N est très utile et apparaît souvent dans ce type de problèmes. En simplifiant le problème en utilisant cette écriture, nous obtenons AB = BA si et seulement si NB = BN. Cette équation plus simple nous permet de trouver une structure pour la matrice B : elle s'écrit sous la forme d'un réel fois I2 plus un réel fois N. Ainsi, l'ensemble des matrices qui commutent avec A peuvent également être écrites de cette manière. Il est important de remarquer que cette méthode est plus efficace et rapide que d'autres approches plus lourdes pour résoudre ce type d'exercice. Il est également recommandé de retenir certaines matrices clés, comme la matrice N, qui apparaissent fréquemment et facilitent les calculs. N'hésitez pas à poser des questions et restez à l'affût des prochaines vidéos.

Equation avec la trace

Dans cet exercice, nous examinons une matrice A de taille n x n dans Mn2R qui vérifie la trace de A x T2A égal à 0. Pour cela, nous utilisons la formule du produit de matrice qui donne les coefficients de la matrice A x B. En utilisant la formule de produit de matrice, nous pouvons calculer A x transposé de A en remplaçant Bkj par son équivalent avec la transposée de A. Ensuite, nous nous concentrons sur les coefficients diagonaux pour calculer la trace égale à zéro. La trace est la somme des coefficients diagonaux, donc nous sommes intéressés par la somme des Aik². En analysant cette somme, nous remarquons qu'elle correspond à la somme de tous les coefficients de la matrice A². Si cette somme est égale à zéro, cela signifie que tous les éléments de la matrice A doivent être nuls ou négatifs. Donc, la condition nécessaire et suffisante pour avoir la trace de A x T2A égal à 0 est que la matrice A soit nulle. En conclusion, la méthode utilisée dans cet exercice démontre que si la trace de A x T2A est nulle, la matrice A doit être nulle.

Centre de Mn

Le cours porte sur la détermination du centre de la matrice Mn2R, qui est l'ensemble des matrices A dans Mn2R telles que A*M = M*A pour toutes les matrices M de Mn2R. Il est tout d'abord mentionné que la matrice identité IN appartient au centre, ainsi que lambda*IN. En d'autres termes, toutes les matrices diagonales avec des coefficients sur la diagonale égales à lambda font partie du centre. Ensuite, le cours explique qu'il faut trouver des conditions sur les coefficients de la matrice A pour qu'elle puisse commuter avec toutes les autres matrices de Mn2R. Pour cela, on peut choisir les matrices EIG de la base canonique de l'espace des matrices, où chaque matrice EIG a des zéros partout sauf un 1 croisant la ligne I et la colonne J. En multipliant A par EIG et en calculant A*M et M*A, on peut déterminer les conditions sur les coefficients de la matrice A. On obtient ainsi que les seules matrices qui commutent avec toutes les autres sont les lambda*IN, c'est-à-dire les matrices diagonales avec des coefficients sur la diagonale égales à lambda. En résumé, le centre de Mn2R est constitué uniquement des matrices diagonales avec des coefficients sur la diagonale égales à lambda.

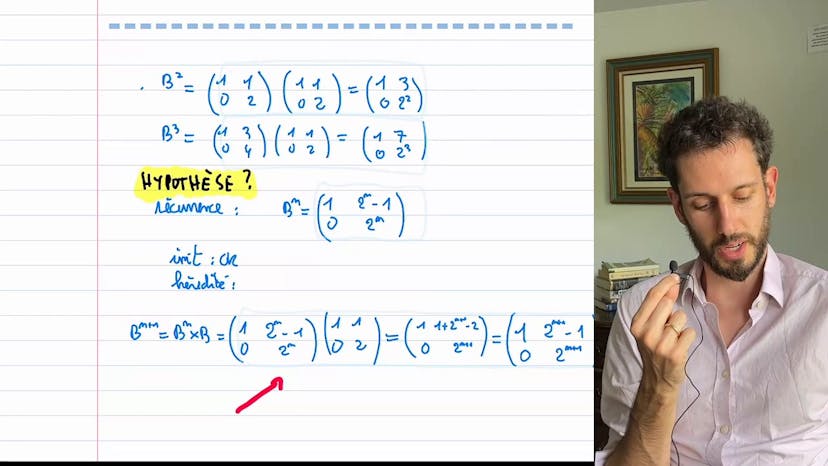
Puissance nième réccurence

Le cours porte sur le calcul de puissances de matrices et l'importance de trouver l'intuition rapidement. L'exemple donné est de calculer A puissance N et B puissance N. Il est recommandé de commencer par calculer les petites puissances pour avoir une idée du résultat. En utilisant la récurrence, on peut déduire que A puissance N est égal à 2 puissance N moins 1 fois A. Pour B, on fait également le même processus et on remarque que le coefficient est proche de 2 puissance N moins 1. On initie le calcul avec B puissance N plus 1 égal B puissance N fois B et cela fonctionne. Il est possible d'essayer différentes hypothèses jusqu'à ce que la récurrence fonctionne. En conclusion, il est important de trouver l'intuition rapidement et de faire des essais par à-coups pour résoudre des problèmes mathématiques.

Puissance nième binome Newton

Ce cours traite de la matrice N, une matrice nilpotente qui finit par s'annuler quand on la monte en puissance. Cette matrice est très importante et intervient dans de nombreux exercices en mathématiques. En la montant en puissance, la diagonale de 1 se déplace jusqu'à disparaître complètement. Cette propriété est valable pour toute dimension de la matrice N. On peut utiliser cette matrice dans des calculs en utilisant le binôme de Newton, en sachant que les termes où B a une puissance supérieure à 3 sont nuls. On peut exprimer cette formule sous forme matricielle en remplaçant les puissances par des matrices N. En résumé, il est important de connaître cette matrice nilpotente dans le domaine des mathématiques.

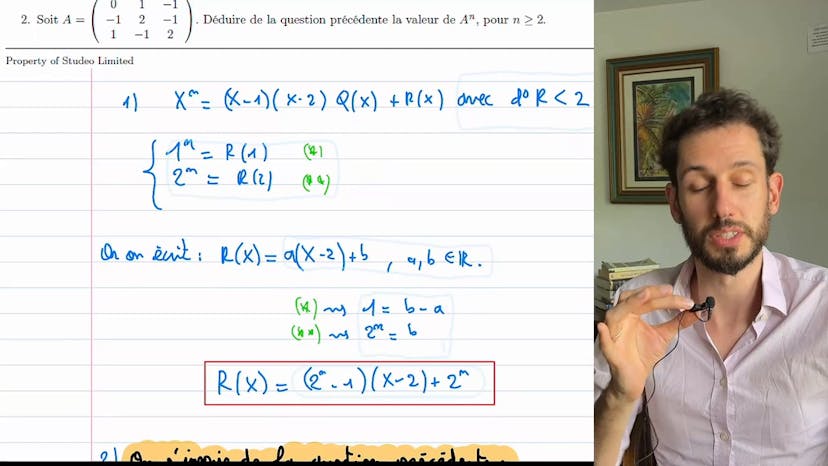
Puissance nième Polynome annulateur

Dans ce cours, on étudie la division euclidienne du polynôme x^n par le polynôme x^2 - 3x + 2. Pour calculer le polynôme reste R2x, on utilise les racines x=1 et x=2 du polynôme diviseur pour éliminer le terme Q2x dans l'équation. On obtient ainsi le polynôme reste R2x qui est de degré 1 et peut s'écrire sous la forme AX + B. En résolvant les équations, on trouve que B=2^n et A=2^n-1. Le polynôme reste R2x peut donc s'écrire comme 2^n-1 * (x-2) + 2^n. Ensuite, on applique cette structure polynomiale à une matrice A. En remarquant que A^2 - 3A + 2I = 0, on déduit que A^n = R2A. Ainsi, on peut calculer A^n en utilisant le polynôme reste R2A qui s'écrit comme 2^n-1 * (A-2I) + 2^n * I.