Cours de Logarithme en Ligne par les Meilleurs Professeurs - Logarithme

Dérivabilité et Variations

Cet article traite de l'étude d'une fonction logarithmique, qui est facile à étudier mais utilise une méthode classique. La fonction proposée est ln2x+1/ln2x-1, définie sur 0 exclu jusqu'à l'infini. La méthode utilisée pour étudier cette fonction est de la dériver, en utilisant la formule g' = u'v - uv' / v², ce qui permet d'obtenir une fonction dérivée de la forme -2x / (ln2x - 1)², qui est strictement négative sur 0e, mais aussi sur e jusqu'à l'infini, sauf en e où elle est indéfinie. Le tableau des variations de la fonction est ensuite déterminé en calculant les limites de la fonction en 0, e-, e+ et à plus l'infini, pour avoir un tableau des variations complet. Il est également noté que la présence de la valeur interdite du logarithme engendre une asymptote verticale en x = e et une asymptote horizontale en y = 1. Enfin, il est souligné que la fonction n'est pas strictement décroissante sur tout l'intervalle.

Croissance Comparée

Dans ce cours, nous analysons la fonction f qui définit la position suivante 3-x + 2ln2x. Nous dérivons la fonction pour trouver son signe et en déduire que la fonction est décroissante sur R étoile plus. En utilisant des croissances comparables, nous trouvons les limites de la fonction à l'infini et à 0. Nous utilisons ces limites pour établir le tableau de variation de f et trouver son extrémum. Ensuite, nous étudions la convexité de f en trouvant la dérivée seconde et en déduisant qu'elle est concave sur R étoile plus tout entier.

Ln : Limites

Nous allons voir comment calculer des limites qui font intervenir la fonction ln. Pour cela, nous allons utiliser le principe de factorisation du terme prédominant et nous allons essayer de nous ramener à des limites usuelles en utilisant les propriétés sur le logarithme.Pour la première limite, nous avons 2 ln(x²) - 5 ln(x) + 1. En factorisant par le terme prédominant ln(x²), nous obtenons 2 - 5/ln(x) + 1/ln²(x), qui tendent toutes vers 0, donc la limite est plus l'infini.Pour la deuxième limite, qui est du ln(√x)/ln(2x), qui tend vers l'infini, nous utilisons les propriétés sur le logarithme pour transformer √x en x^(1.5) et obtenir 1.5 ln(x)/ln(2) + ln(x)/ln(2). En factorisant par le terme prédominant ln(x), nous obtenons 1.5 + ln(2)/ln(x), qui tend vers 1.5.Enfin, pour la dernière limite, qui est (x-1)² ln(x-1) quand x tend vers 1, nous posons grand x = x-1 pour obtenir x² ln(x). En séparant le x, nous obtenons x * x ln(x), qui tend vers 0, donc la limite recherchée est égale à 0.Si vous avez des questions, n'hésitez pas à consulter la FAQ.

Dériver ln(u)

Ce cours aborde la méthode pour déterminer l'ensemble de définition d'une fonction avec logarithme et calculer sa dérivée. Il est important de bien regarder l'ensemble de définition d'une expression, notamment pour une inégalité. La première fonction est f(x) = ln(8x-4), pour laquelle l'ensemble de définition est 1/2 à l'infini et la dérivée est 2/(2x-1). La deuxième fonction est f(x) = ln(x^2 + x + 1), qui est définie et dérivable sur R tout entier et la dérivée est 2x/(x^2 + x + 1). La troisième fonction est f(x) = ln(u/v), avec u(x) = x-1 et v(x) = 2x+4. L'ensemble de définition est (-∞, -2) U (1, +∞) et la dérivée est (6/(v(u-v))(u/v)). Finalement, la quatrième fonction est f(x) = ln(e^x / e^0.1x), qui est définie et dérivable sur R+ étoile et la dérivée est e^x / e^0.1x. Il est important de mémoriser de toujours vérifier l'ensemble de définition pour une expression impliquant une fonction logarithmique.

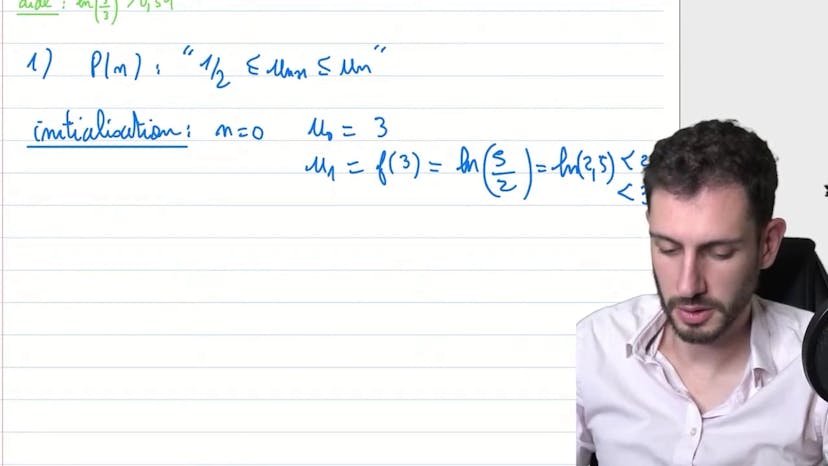
Fonction et suite récurrente associée

Dans ce cours, nous étudions une fonction définie par une fraction rationnelle avec un degré de 1 au-dessus et en-dessous de la barre de fraction. La fonction est définie sur l'intervalle de 0 à l'infini. Nous déterminons la limite de la fonction lorsque x tend vers l'infini et interprétons graphiquement cette limite comme un plateau atteint par la fonction à mesure que x tend vers l'infini. Ensuite, nous démontrons que la dérivée de la fonction est égale à une expression donnée pour tout nombre réel positif ou nul. Nous utilisons des transformations mathématiques pour simplifier le calcul de la dérivée. Nous concluons en disant que la fonction est strictement croissante et positif sur son ensemble de définition. Dans la deuxième partie du cours, nous étudions une suite définie par récurrence à l'aide de la fonction précédemment étudiée. Nous démontrons par récurrence que la suite est décroissante et minorée. Nous utilisons des calculs numériques pour vérifier l'initialisation de la récurrence et la propriété héréditaire. Enfin, nous concluons en disant que la suite converge vers une limite strictement positive en utilisant le théorème des suites décroissantes et minorées.