Cours de Complexes en Ligne par les Meilleurs Professeurs - Complexes

Parties réelle et imaginaire

Ce cours porte sur les complexes et vise à vérifier les affirmations suivantes. Premièrement, en utilisant la forme algébrique, la somme de la partie réelle des nombres complexes est égale à la partie réelle de la somme. Deuxièmement, la partie réelle de iz est égale à moins la partie imaginaire de z. Troisièmement, pour tout lambda appartenant à R, la partie imaginaire de lambda z est égale à lambda fois la partie imaginaire de z. Quatrièmement, la partie imaginaire du produit de nombres complexes ai n'est pas égale au produit des parties imaginaires. Enfin, si z est différent de 0, 1 sur z est égal au conjugué de z divisé par le module au carré de z, et la partie imaginaire de z divisé par w n'est pas égale à la partie imaginaire de z divisé par la partie imaginaire de w.

Forme algébrique

Cet exercice consiste à transformer des complexes sous forme algébrique en utilisant la technique de multiplication par le conjugué du dénominateur lorsque des i apparaissent à ce niveau. Ensuite, le module carré du complexe est obtenu en faisant la somme des carrés des parties imaginaires et réelles, ce qui permet de simplifier les fractions et de rassembler les résultats pour obtenir la forme algébrique finale. La vidéo montre également une méthode alternative, consistant à poser des variables et à utiliser des symétries pour résoudre le calcul.

Module

Cet exercice en mathématiques démontre que pour tout u et v dans C, l'équation suivante est vraie : le module de u plus v au carré plus le module de u moins v au carré est égal à deux fois le module de u au carré plus le module de v au carré. La formule fondamentale utilisée est que le module de z au carré est égal à z fois son conjugué. Pour prouver cette équation, on part du membre de gauche en utilisant cette formule pour développer et simplifier, puis réutilisons la formule pour arriver à notre résultat final. En conclusion, cette équation est vraie pour tout u et v dans C.

Inégalité triangulaire, partie réelle et imaginaire d’un quotient

Paul explique comment résoudre un exercice sur les complexes en suivant les étapes suivantes : 1. Établir l'inégalité triangulaire renversée.2. Exprimer la partie réelle et la partie imaginaire d'un complexe en fonction des parties réelles et imaginaires de ce complexe ainsi que du module de ce complexe.3. Utiliser les formules de l'air pour calculer la partie réelle et la partie imaginaire d'un nombre complexe. Il rappelle l'importance de bien visualiser les angles et les formes exponentielles et de prendre les formules de l'air par cœur.

Formule de l'arc moitié

Le cours explique comment transformer des nombres complexes en forme exponentielle en factorisant par eit plus eit prime sur 2 à l'aide de la méthode de l'angle moitié. Il montre également comment vérifier si le nombre obtenu est positif en utilisant la fonction cosinus et dans quelles conditions rajouter un pi à l'argument. L'application pratique est présentée pour les nombres 1 et -1.

Racine n-ième

Dans cette leçon, Paul résout des équations avec des nombres complexes en utilisant la forme exponentielle. Il explique comment mettre des nombres complexes sous forme exponentielle en utilisant les valeurs des sinus et des cosinus sur le cercle trigonométrique. Il montre comment résoudre des équations avec des racines de l'unité en divisant un nombre complexe par lui-même et en le faisant passer dans l'ensemble des racines de l'unité. Enfin, il rappelle qu'une équation de ce type aura généralement quatre à six solutions.

Formule de Moivre

Dans cette vidéo, Paul explique comment calculer exponentielle de e i alpha et comment traiter différents cas pour les formes exponentielles de nombres complexes. Il insiste sur la compréhension de la notation et la distinction entre exponentielle de e i alpha et exponentielle puissance e, le tout puissance i alpha. Il montre ensuite comment exprimer e i alpha en forme module argument et comment prendre en compte les cas où le module est égal à 0 ou l'argument n'existe pas. Il explique également comment obtenir l'argument d'un produit de nombre complexe et quand il est positif ou négatif. Tout cela est présenté de manière claire et structurée pour une meilleure compréhension.

Produit des racines de l'unité

Dans cette vidéo, Paul explique un exercice qui implique le calcul d'un produit de ω et k, pour k allant de 0 à n-1. Il montre que ce produit est égal à a-1 puissance n-1 avec les ω égales E2i pi sur n. Paul explique que les racines n° de l'unité, ω0, ω1, ω2 jusqu'à ωn-1, ainsi que la somme des racines n° de l'unité peuvent être utiles dans ce calcul. Il souligne également l'utilisation de la formule qui dit qu'un produit d'exponentielles s'égale à l'exponentielle de la somme. En remplaçant ωk par sa valeur exponentielle de 2ikπ sur n, on obtient eipi puissance n-1 qui est égal à -1. Le résultat attendu est donc confirmé.

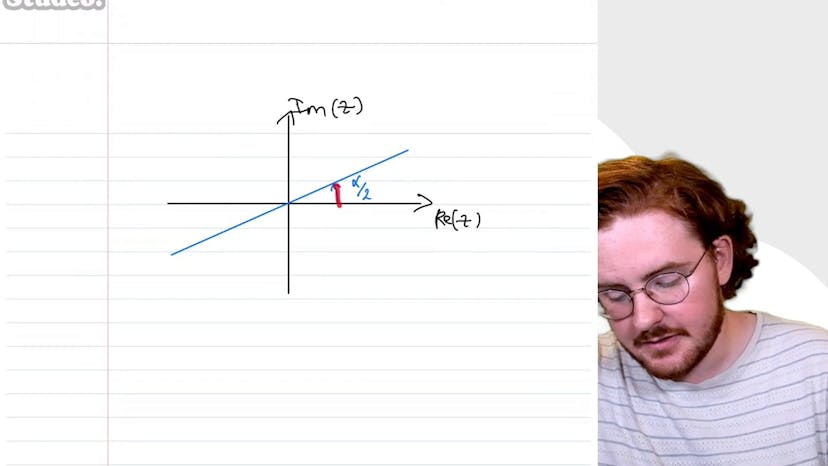
Alignement de points

Dans ce cours, Paul explique une méthode avancée pour résoudre des équations complexes. Il utilise une équation classique à résoudre pour trouver des racines d'une équation complexe. Ensuite, il prouve que les affixes de ces racines sont alignées en utilisant deux cas : la droite qui passe par l'origine et la droite qui ne passe pas par l'origine. On utilise la technique de l'angle moitié pour prouver que toutes les affixes des complexes sont alignées sur une droite décalée de alpha sur 2.

Sommes trigonométriques

Le cours explique l'utilisation des nombres complexes dans le calcul de sommes, notamment avec les fonctions trigonométriques. Pour calculer les sommes, l'orateur utilise la méthode du binôme de Newton et la somme des termes d'une suite géométrique. Il rappelle également l'utilisation des parties réelles et imaginaires pour bien séparer les sommes. La dernière question aborde un cas où il faut d'abord calculer dn en fonction de n et le remplacer ensuite par k, sans oublier de remplacer tous les n par les k. Enfin, l'orateur souligne que les complexes sont indispensables dans le calcul des sommes avec des fonctions trigonométriques pour éviter les erreurs.

Équations polynomiales

Dans cette vidéo, Paul explique comment résoudre des équations du second degré à coefficients complexes, ainsi que des équations qui s'en rapprochent. Pour la première équation, la technique est similaire à la résolution d'une équation réelle, en trouvant les valeurs de Z1 et Z2. Pour la deuxième équation, qui est déguisée en une équation du second degré, Paul pose X = Z3 et résout l'équation pour trouver les solutions de X. Ensuite, il résout l'équation E1 pour trouver les solutions de Z3, en utilisant la racine 1ème de l'unité. Au final, il obtient 6 solutions qui correspondent au polynôme initial de degrés 6.