Cours d'apprentissage en ligne

Définition du nombre dérivé

Aucun résumé n'est disponible pour cette vidéo

Dans ce cours, nous nous intéressons à la dérivabilité en un point lorsque les fonctions ont différentes expressions sur leur ensemble de définition. Nous commençons par l'exemple classique de la fonction sin(x)/x, qui n'est pas définie en zéro car on ne peut pas diviser par zéro. Cependant, cette fonction tend vers 1 lorsque x tend vers zéro, donc nous pouvons "prolonger" la fonction en zéro en posant f(0)=1. Ensuite, nous nous demandons si cette fonction est dérivable en zéro. Pour répondre à cette question, nous utilisons la définition de la dérivabilité et calculons le taux d'accroissement, qui s'avère être 1. Ainsi, la fonction est bien dérivable en zéro. Ensuite, nous étudions deux autres exemples de fonctions avec des expressions différentes sur leur ensemble de définition. Dans le premier exemple, la fonction est x/(1+|x|). Nous remarquons que cette fonction est continue partout sauf en zéro, où |x| n'est pas dérivable. Pour savoir si la fonction est dérivable en zéro, nous devons utiliser la définition et calculer le taux d'accroissement, qui tend vers 1. Par conséquent, la fonction est bien dérivable en zéro. Dans le deuxième exemple, la fonction est xsin(x)sin(1/x), avec g(0)=0. Nous constatons que cette fonction est continue, mais nous devons utiliser la définition de la dérivabilité pour savoir si elle est dérivable en zéro. En calculant le taux d'accroissement, nous obtenons sin(x)sin(x), qui tend vers zéro. Cependant, sin(x) n'a pas de limite, ce que nous prouvons en montrant qu'il existe des valeurs de x pour lesquelles sin(1/x) = 1 ou -1. Par conséquent, nous concluons que la fonction g n'est pas dérivable en zéro. Enfin, nous examinons un dernier exemple, la fonction |x|sin(x). Cette fonction est parfaitement définie, mais |x| n'est pas dérivable en zéro. En utilisant la définition de la dérivabilité, nous calculons le taux d'accroissement, qui tend vers zéro. Par conséquent, la fonction h est dérivable en zéro et h'(0)=0. En résumé, pour déterminer si une fonction est dérivable en un point lorsque les fonctions ont différentes expressions sur leur ensemble de définition, nous devons recalculer le taux d'accroissement en utilisant la définition de la dérivabilité. C'est ainsi que nous pouvons dire si la fonction est dérivable ou non. La question de savoir si la dérivée est continue sera abordée dans d'autres méthodes.

Dérivée n-ième

Dans ce cours, nous apprenons comment appliquer la formule de Leibniz pour calculer les dérivées d'ordre supérieur. Nous prenons comme exemple une fonction produit composée d'un polynôme et d'une exponentielle. Tout d'abord, il est important de justifier que cette fonction est dérivable à l'ordre n. Ensuite, nous appliquons la formule de Leibniz qui dit que la dérivée d'ordre n est égale à la somme des combinaisons possibles entre les dérivées km du polynôme et les dérivées n-km de l'exponentielle. Il faut noter que les dérivées d'ordre supérieur du polynôme sont toutes nulles à partir de la dérivée troisième. Donc, il est plus simple de choisir de dériver n-km fois le polynôme. Finalement, nous simplifions l'expression en factorisant par e^-x et en effectuant les calculs. Il est important de repérer les cas où les dérivées d'une des fonctions deviennent nulles, car cela simplifiera grandement l'expression finale. C'est ainsi que nous maîtrisons et utilisons la formule de Leibniz pour calculer les dérivées d'ordre supérieur.

Utiliser la définition formelle de limite

Le cours porte sur les dérivés et explique la définition formelle de la dérivée comme étant la limite du taux d'accroissement. On applique cette définition à une méthode de base pour calculer la dérivée. Ensuite, on se demande si une limite parfaitement définie implique nécessairement la dérivabilité de la fonction. On utilise une astuce de décomposition du taux d'accroissement pour montrer que la réciproque est fausse. On prend l'exemple de la valeur absolue qui n'est pas dérivable en 0, malgré une limite parfaitement définie qui vaut 0. Ainsi, on montre comment utiliser la définition formelle de la dérivée.

Sens de variation

Aucun résumé n'est disponible pour cette vidéo

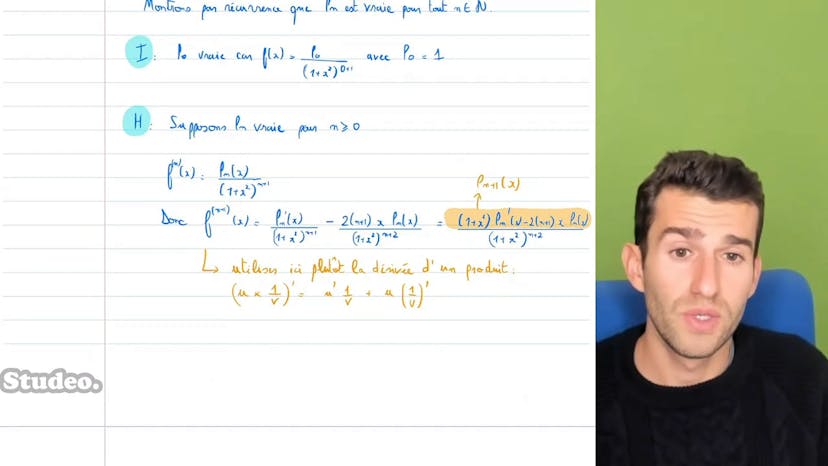
Dérivée n-ième difficile

Dans ce cours, nous étudions la dérivée n-ième d'une fonction en utilisant la formule de Leibniz. Nous cherchons à trouver des relations récursives entre les dérivées n-ièmes successives. La question principale est de savoir à quoi ressemble la dérivée n-ième de la fonction f(x) = e^x + x^2. Nous voulons montrer que cette dérivée peut être exprimée sous la forme d'un polynôme Pn(x) = 1 + x^2)^n+1. Pour cela, nous utilisons une récurrence et nous essayons de trouver une relation entre Pn+1(x) et Pn(x) en utilisant la dérivée de Pn(x). Il s'avère que trouver directement Pn(x) est fastidieux, mais nous trouvons une relation en dérivant n fois la fonction f(x) et en simplifiant les termes. En utilisant la formule de Leibniz, nous trouvons une expression plus simple pour Pn'(x) en fonction de Pn-1(x). Après avoir initialisé la récurrence et montré l'hérédité, nous dérivons l'expression de Pn+1(x) et simplifions les termes. Finalement, nous obtenons une expression pour Pn'(x) en utilisant la formule de Leibniz. En dérivant l'expression n fois, nous trouvons que la dérivée n-ième de f(x) est égale à une somme de termes impliquant Pn(x), Pn-1(x) et Pn-2(x). En remplaçant les expressions de Pn+1(x), Pn(x) et Pn-1(x), nous obtenons une relation finale entre Pn'(x) et Pn-1(x). Bien que les calculs puissent paraître complexes, la formule de Leibniz avec des polynômes nous permet de simplifier les termes jusqu'à obtenir des relations claires entre les dérivées n-ièmes successives.

Tangente commune

Ce cours traite des tangentes et de l'utilisation de la dérivée. L'exercice présenté concerne deux courbes, y égal x carré et y égal 1 sur x, et l'objectif est de montrer qu'elles ont une tangente commune. Il est important de noter que tangente commune ne signifie pas qu'elles sont tangentes au même point, mais plutôt qu'elles partagent une droite commune, avec le même coefficient directeur et la même ordonnée à l'origine. Pour cela, il est nécessaire d'obtenir l'expression générale des tangentes pour chacune des courbes. En utilisant la dérivée, on obtient les équations des tangentes. En résolvant les équations, on trouve qu'il y a une seule tangente commune avec une abscisse de -2 et une ordonnée de -1,5. L'équation de cette droite est y égal moins 4x moins 4. Ce cours met en évidence l'importance de bien comprendre et maîtriser les notions de tangentes et de dérivées.

Introduction à la récurrence

Dans cette vidéo, le cours introduit le principe de la méthode de démonstration par récurrence, en se basant sur l'exemple de la formule de la somme des n entiers consécutifs. La méthode de démonstration par récurrence s'applique uniquement aux propriétés dépendant de n. Il est important de noter que la méthode de récurrence ne fournit pas une formule, mais plutôt une manière de démontrer une formule dont on a déjà une intuition. Pour démontrer la propriété, on commence par une initialisation, où la propriété est vérifiée pour une valeur spécifique de n. Ensuite, on prouve que si la propriété est vraie pour un certain n, alors elle est également vraie pour n+1, ce qui permet de conclure que la propriété est vraie pour tous les entiers. Il est crucial de ne pas oublier cette initialisation, car sans elle, la méthode de récurrence ne fonctionnera pas. Le cours souligne également trois points clés à retenir : le principe général de la récurrence (initialisation et hérédité), l'importance de l'initialisation (qui peut commencer à n=0, n=1, etc.) et l'inégalité de Bernoulli, qui peut être démontrée par récurrence. En termes de méthode, la récurrence peut être appliquée aux suites, utilisée pour démontrer une formule générale basée sur quelques termes, ou pour résoudre des problèmes plus complexes nécessitant différentes approches de la transmission.

Concept et rédaction

Dans cette vidéo, le professeur explique le principe de la récurrence en mathématiques. Il rappelle que pour démontrer une propriété par récurrence, il faut montrer qu'elle est vraie pour un entier donné, puis que si elle est vraie pour cet entier, elle est également vraie pour l'entier suivant. En utilisant cette "pichenette initiale" et cette transmission, on peut prouver que la propriété est vraie pour tous les entiers. Le professeur insiste sur l'importance de la rédaction dans la démonstration par récurrence. Il souligne qu'il faut toujours conclure la démonstration en affirmant que la propriété est vraie pour tout entier. Si cette conclusion n'est pas incluse, il est possible de perdre des points. Il recommande ainsi de donner une vision d'ensemble de la démonstration après avoir montré l'initialisation et la transmission de la propriété. Le professeur mentionne également que dans environ 10% des exercices, la démonstration par récurrence commence avec un entier différent de zéro, ce qui peut dérouter les étudiants. Il donne l'exemple d'une suite récurrente où il faut prouver la propriété pour tout entier supérieur à 2, au lieu de 0. Enfin, le professeur rappelle aux étudiants de se référer aux consignes spécifiques de leur professeur concernant la rédaction de la démonstration par récurrence, afin d'obtenir de bons résultats. Il invite également les étudiants à poser leurs questions dans la FAQ du cours pour obtenir des éclaircissements supplémentaires.

Pourquoi l'initialisation ?

Dans cette vidéo, on aborde l'importance de l'initialisation dans le contexte de la transmission de propriétés. L'orateur mentionne un exemple spécifique, celui de la propriété P2N, qui affirme que 2 puissance N est divisible par 3, bien que cela soit incorrect. Cependant, cette propriété est transmise, c'est-à-dire que si elle est vraie pour un instant N, elle le sera également pour l'instant N+1. Cela souligne l'importance de l'initialisation, même si celle-ci peut sembler fastidieuse. L'orateur conclut en expliquant qu'il est crucial de faire les initialisations nécessaires pour chaque propriété, car il est peu probable de trouver une initialisation pour des propriétés comme P2N. Cette vidéo est un bonus pour les étudiants, leur montrant que les professeurs insistent sur l'initialisation non pas pour les embêter, mais parce qu'il y a des implications importantes derrière cela. N'hésitez pas à poser des questions ou à consulter la FAQ ci-dessous.

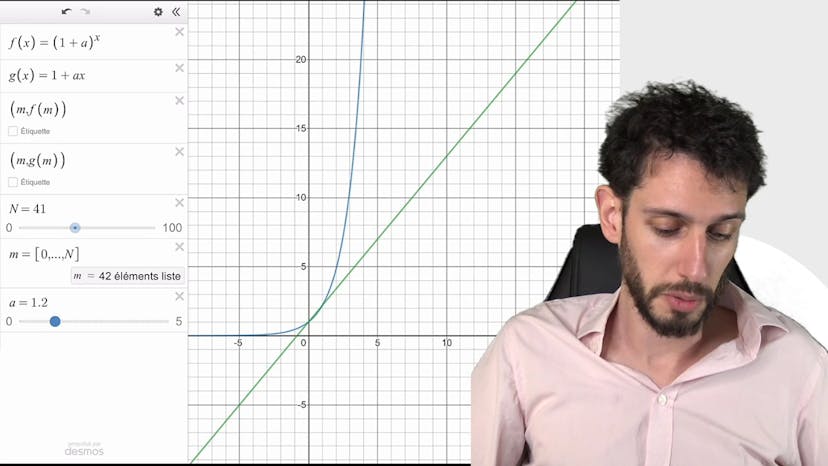
Inégalité de Bernoulli : visuel

Dans cette vidéo, le professeur explique l'inégalité de Bernoulli, qui stipule que pour toute valeur réelle A strictement positive et pour tout entier naturel N, on a l'inégalité 1 + A^N ≥ 1 + NA. Il mentionne que cette inégalité est étudiée dans le cadre de la récurrence car elle peut être démontrée de manière simple en utilisant le principe de récurrence. Pour donner une intuition graphique de cette formule, le professeur compare les deux éléments de l'inégalité à des fonctions. Il remarque que la partie de gauche, A^N, a une forme exponentielle, tandis que la partie de droite, NA, a une forme affine. Il explique que cela traduit le fait qu'une fonction exponentielle monte beaucoup plus vite qu'une fonction affine et donc est plus grande. Pour illustrer cette idée, le professeur utilise une simulation graphique où il fait varier différents paramètres, notamment la valeur de A. Il montre que pour certaines valeurs de A, la fonction exponentielle est toujours au-dessus de la fonction affine, tandis que pour d'autres valeurs, la fonction affine dépasse la fonction exponentielle dans un certain intervalle. Cependant, il souligne que cela n'est pas important pour l'inégalité de Bernoulli, car ce qui compte, c'est la suite des points représentés par les coordonnées entières des fonctions. En observant les points de la suite définie par les fonctions, le professeur constate que, dès le point 2, la suite représentée par la fonction exponentielle est toujours au-dessus de celle représentée par la fonction affine. Il mentionne également que pour les entiers 0 et 1, les deux fonctions sont égales, ce qui peut être vérifié en remplaçant ces valeurs dans l'inégalité de Bernoulli. Le professeur conclut en soulignant l'utilité de cette inégalité pour les démonstrations mathématiques et invite les spectateurs à poser des questions et utiliser la simulation graphique partagée pour mieux comprendre l'inégalité de Bernoulli.