Cours d'apprentissage en ligne

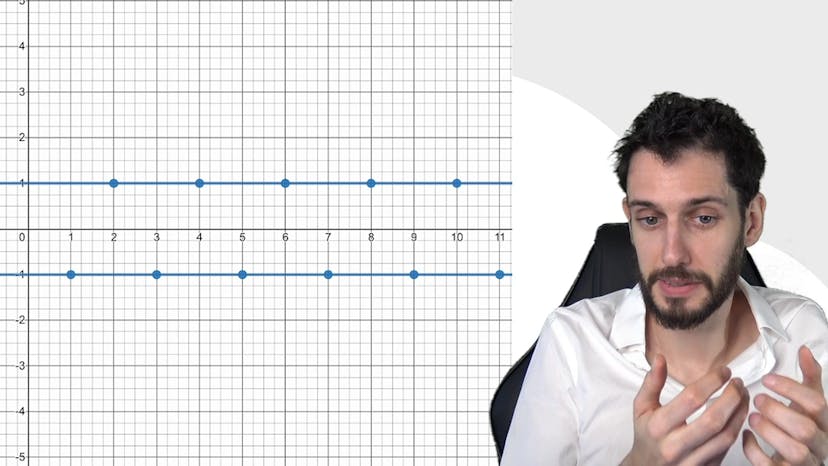
Unicité et divergence

Dans cette vidéo, on aborde la convergence et les limites en mathématiques. Il y a deux points importants à retenir. Le premier est que lorsqu'une limite est finie, elle est unique. En d'autres termes, on ne peut se rapprocher que d'une seule valeur. Le deuxième point concerne le vocabulaire utilisé. On utilise le terme "convergence" pour décrire une suite qui a une limite finie. Cependant, il est important de noter que ne pas être convergent ne signifie pas automatiquement tendre vers l'infini. Il est possible de diverger d'une autre manière. Un exemple de divergence est donné avec la suite "-1 puissance n". Cette suite oscille entre -1 et 1 et ne tend ni vers l'infini ni vers moins l'infini. On peut dire qu'elle a un comportement d'oscillation permanent. On peut également extraire des sous-suites à partir de cette suite pour observer des convergences partielles, mais dans son ensemble, la suite n'a pas de limite. En conclusion, il est important de comprendre que la convergence en mathématiques ne se limite pas seulement à tendre vers l'infini ou moins l'infini. Il existe des cas de divergence avec des comportements d'oscillation permanente. Pour plus de détails et d'informations, vous pouvez consulter la FAQ ou discuter avec nous.

Références et opérations

Lorsque nous étudions la convergence et la divergence de suites vers une limite finie ou infinie, il y a différentes règles et outils à connaître. Tout d'abord, les puissances de n tendent vers l'infini lorsque n tend vers l'infini. Par exemple, n, n², n³, etc. tendent tous vers l'infini. Il est important de noter que cette règle s'applique également aux puissances non-entières, telles que la racine de n, qui peut être écrite comme n puissance 1,5. En général, les puissances positives de n, quelle que soit la valeur de k (entier ou rationnel), tendent vers l'infini. De plus, il est important de comprendre que plus la puissance augmente, plus la suite tend vers l'infini rapidement. Par exemple, n³ augmente plus rapidement que n². En ce qui concerne les puissances négatives de n, c'est-à-dire 1/n, elles tendent toutes vers zéro. En divisant 1 par un nombre très grand, nous obtenons un nombre très petit, proche de zéro. Ensuite, il est essentiel de savoir comment gérer les opérations sur différentes suites. Par exemple, si nous connaissons les limites de deux suites, pouvons-nous déterminer la limite de leur somme ? Dans la plupart des cas, la réponse est oui. Il existe une règle prédéterminée selon laquelle si une suite tend vers l et une autre vers l', leur somme tend vers l + l'. Si l'une des suites tend vers plus ou moins l'infini et l'autre vers une limite finie, c'est l'infini qui l'emporte. Si les deux suites tendent vers plus ou moins l'infini, leur somme tend également vers plus ou moins l'infini. Cependant, il existe des situations plus complexes appelées "formes indéterminées", pour lesquelles il n'y a pas de règle prédéterminée. Dans ces cas, il faut analyser la situation au cas par cas. Par exemple, si une suite tend vers l'infini et une autre vers moins l'infini, la somme peut être égale à zéro ou à l'infini, selon les valeurs spécifiques des suites. Il est donc important de comprendre qu'il existe des formes indéterminées et de savoir les reconnaître lorsqu'elles se présentent. Il y a également des formes indéterminées pour les produits de suites, par exemple lorsque l'une tend vers zéro et l'autre vers l'infini. Il faut faire attention à ces situations et les analyser individuellement. Pour les quotients de suites, il peut y avoir deux formes indéterminées : plus l'infini sur plus l'infini et zéro sur zéro. Il est donc nécessaire de prêter une attention particulière à ces cas. En conclusion, il est important de mémoriser les règles et les formes indéterminées associées à la convergence et à la divergence des suites. De plus, il est crucial d'appliquer ces connaissances lors de la résolution d'exercices.

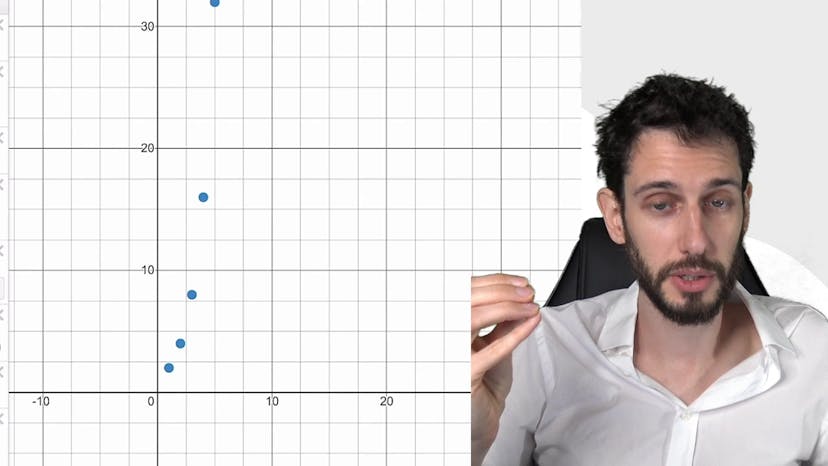
Suites géométriques - Illustration

Dans cette vidéo, nous abordons les concepts de convergence et de divergence des suites géométriques. Une suite géométrique est définie par une raison, notée Q, et peut avoir différents comportements en fonction des valeurs de cette raison. Lorsque Q est strictement supérieur à 1, la suite tend vers l'infini. Par exemple, si nous prenons Q égal à 3, nous obtenons une suite qui augmente rapidement : 3, 9, 27, 81, etc. Ce comportement peut être démontré à l'aide de l'égalité de Bernoulli. Lorsque Q est compris entre -1 et 1, la suite converge vers zéro. Par exemple, si nous prenons Q égal à 0,5, nous obtenons une suite qui diminue progressivement : 0,5, 0,25, 0,125, etc. L'intuition derrière cela est que la raison Q, plus petite que 1, enlève un petit bout à chaque terme précédent, conduisant finalement à zéro. Si Q est égal à 1, la suite est constante et égale à 1. Si Q est inférieur à -1, la suite diverge, mais d'une manière différente. Dans ce cas, la suite ne converge ni vers l'infini ni vers moins l'infini, mais oscille entre des valeurs positives et négatives. Par exemple, si nous prenons Q égal à -0,7, nous obtenons une suite qui oscille autour de zéro sans converger vers une valeur spécifique. Ces différents comportements peuvent être illustrés graphiquement. Par exemple, la suite 2^n augmente rapidement et converge vers l'infini. Les suites avec une raison entre -1 et 1, comme 0,7^n, diminuent progressivement et convergent vers zéro. Les suites avec une raison inférieure à -1, comme -0,7^n, oscillent autour de zéro sans converger vers une valeur précise. Il est essentiel de comprendre visuellement ces différents cas afin de saisir les concepts de convergence et de divergence des suites géométriques. Dans la prochaine vidéo, nous aborderons les démonstrations mathématiques de ces comportements.

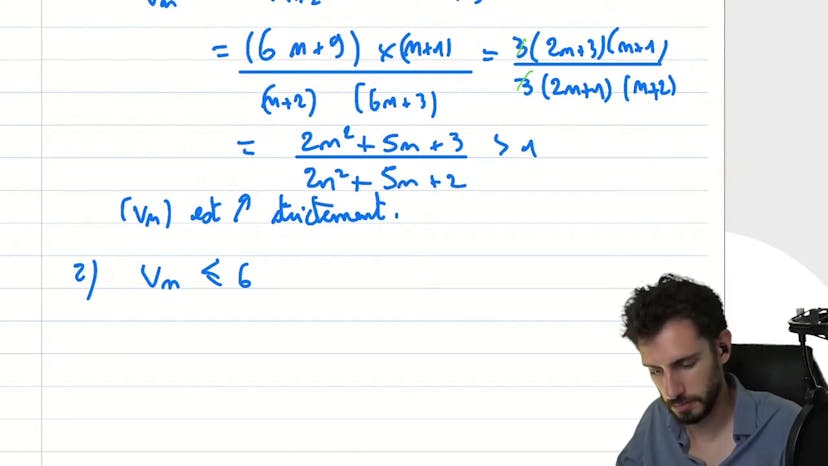
Essai limites

La suite vn = 6n + 3 / n + 1 est étudiée pour déterminer ses variations et sa convergence. Pour cela, deux méthodes sont utilisées. Méthode 1: Les variations de la suite sont étudiées en utilisant le critère de croissance. On montre que le ratio vn+1 / vn est strictement supérieur à 1, ce qui implique que la suite est croissante. Ensuite, on démontre que la suite est majorée par 6, ce qui permet de conclure que la suite convergente. Méthode 2: On simplifie l'expression de vn en forçant l'apparition de n+1 au numérateur. On obtient vn = 6n + 3 / n + 1 = (6n + 6 - 3) / (n + 1) = (6(n + 1) - 3) / (n + 1) = 6 - 3 / (n + 1). En analysant cette nouvelle expression, on conclut que la suite est croissante, positivement bornée par 6, et converge vers 6. En résumé, la suite vn = 6n + 3 / n + 1 est croissante, majorée par 6, et converge vers 6.

Limite finie

Dans cette vidéo, nous abordons la définition des limites en mathématiques. Une limite réelle est la valeur vers laquelle une séquence tend au fur et à mesure que n augmente. Pour expliquer cette notion, on utilise celle de couloir. Nous présentons deux aspects : tout d'abord, une explication détaillée du concept de couloir entourant la limite, puis nous montrons que la convergence peut se faire de manière régulière (croissante, décroissante) ou plus chaotique (oscillante). La définition officielle stipule qu'une séquence converge vers une limite L si, pour tout intervalle autour de L, tous les termes de la séquence finissent par être compris dans cet intervalle à un certain moment. Sur un graphique, nous observons une séquence donnée entourée d'un couloir représentant la limite. On vérifie que tous les termes de la séquence sont inclus dans le couloir à partir d'un certain point. Si cette propriété est vérifiée pour tous les intervalles, alors L est bien une limite. Nous examinons différents exemples pour illustrer les différentes façons de converger vers une limite : une séquence croissante, une séquence décroissante et une séquence oscillante. Nous soulignons que la notion de couloir permet d'englober ces différentes situations. Cette vidéo fournit un aperçu de la définition des limites et présente des exemples graphiques pour faciliter la compréhension. N'hésitez pas à consulter la FAQ pour poser des questions ou obtenir des éclaircissements. Rejoignez-nous dans la prochaine vidéo pour continuer notre exploration des limites.

En l'infini

Dans ce cours, nous abordons les limites infinies. On dit qu'une suite "un" tend vers plus l'infini si, pour n'importe quel plateau A, il existe un rang n à partir duquel tous les termes de la suite sont supérieurs à A. Cela signifie que la suite peut dépasser n'importe quel plateau et continuer à croître. Cette idée est illustrée graphiquement avec une suite croissante basée sur la parabole x². On peut constater que pour n'importe quel plateau, comme 8 ou 50, il existe un rang à partir duquel tous les termes de la suite sont au-dessus de ce plateau. Nous appelons cela une limite vers plus l'infini. Pour la limite vers moins l'infini, nous utilisons une suite décroissante, l'inverse de la première. Encore une fois, on peut constater graphiquement que pour n'importe quel plateau, comme -45 ou 60, il existe un rang à partir duquel tous les termes de la suite sont en dessous de ce plateau. Cela signifie que la suite peut passer sous n'importe quel plateau. Nous appelons cela une limite vers moins l'infini. Il est important de comprendre ces concepts graphiques pour pouvoir les utiliser dans des exercices et méthodes classiques. Si vous avez des questions, n'hésitez pas à les poser dans la FAQ.

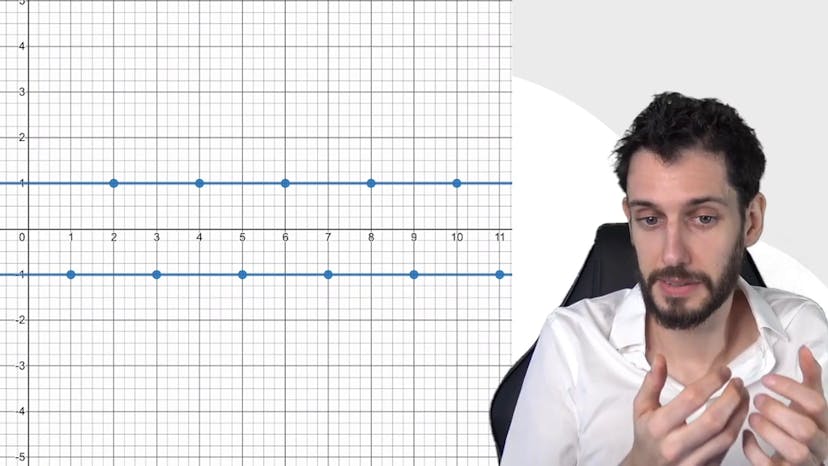
Unicité et Divergence

Nous pourrions résumer ce cours sur la convergence en mettant l'accent sur deux points clés. Tout d'abord, une limite finie est unique, ce qui signifie que lorsque nous nous approchons d'une valeur, nous ne pouvons pas nous approcher de deux valeurs différentes. Ensuite, nous devons faire attention à ne pas confondre convergence et tendance vers l'infini ou moins l'infini. Être divergent, c'est-à-dire non convergent, ne signifie pas automatiquement se diriger vers l'infini. Il existe de cas de divergence où les valeurs oscillent sans converger vers une limite finie. Par exemple, une suite telle que (-1)^n oscille entre 1 et -1 sans convergence. Il est important de noter que bien que certains termes de la suite puissent sembler converger vers 1, il n'y a pas de limite globale et la suite ne converge ni vers l'infini, ni vers moins l'infini. Si vous avez besoin de plus de détails, veuillez consulter notre FAQ ou discuter avec nous. À la prochaine !

Limites de référence et opérations

Lorsque nous examinons les limites finies ou infinies en mathématiques, il est important de connaître certains outils pratiques. Le programme insiste sur le fait que les puissances de "n" tendent vers l'infini lorsque "n" tend vers l'infini. Par exemple, les puissances de "n", telles que "n²" ou "n³", tendent toutes vers l'infini. Il est important de noter que cette règle s'applique non seulement aux puissances entières, mais également aux racines de "n", comme la racine carrée de "n" que l'on peut écrire comme "n" puissance 1,5. De plus, il est essentiel de comprendre que les puissances de "n" tendent de plus en plus rapidement avec l'augmentation de la puissance. Par exemple, "n³" augmente plus rapidement que "n²". Un autre outil important concerne les opérations sur différentes suites. Par exemple, si nous connaissons les limites de deux suites, pouvons-nous déterminer directement la limite de leur somme ? Dans la plupart des cas, oui. Il existe une règle prédéterminée selon laquelle si une suite tend vers "l" et une autre tend vers "l'", la somme des deux tendra vers "l + l'". Il est important de comprendre que lorsque l'une des suites tend vers plus ou moins l'infini et que l'autre tend vers une limite finie, l'infini l'emporte. De même, lorsque les deux suites divergent vers plus ou moins l'infini, leur somme suivra cette tendance. Cependant, lorsqu'il s'agit d'une combinaison spécifique, appelée "forme indéterminée", il n'y a pas de règle prédéterminée. Il est nécessaire d'examiner chaque cas individuellement. Il existe différentes formes indéterminées, telles que la somme de deux suites tendant vers l'infini et moins l'infini, le produit d'une suite tendant vers zéro et une autre tendant vers l'infini, et le quotient de deux suites tendant vers plus ou moins l'infini ou zéro sur zéro. Il est crucial de reconnaître ces formes indéterminées et de savoir comment les aborder lorsqu'elles se présentent dans un exercice. En conclusion, il est recommandé d'apprendre les tables correspondantes, de retenir les règles sur les puissances de "n" et de se familiariser avec les formes indéterminées. En les connaissant et en les comprenant, on sera prêt pour les exercices. N'hésitez pas à consulter les ressources supplémentaires si vous avez des questions ou besoin de précisions.

Suites géométriques - illustration

Dans cette vidéo, nous explorons la convergence et la divergence des suites géométriques. Une suite géométrique est définie par une raison Q, et selon les valeurs de cette raison, elle peut avoir différents comportements. Nous commençons par illustrer et comprendre intuitivement ces comportements. Lorsque Q est supérieur à 1, la suite tend vers l'infini. Par exemple, si Q est égal à 3, les termes de la suite augmentent rapidement. Ce comportement peut être démontré avec l'inégalité de Bernoulli. Lorsque Q est entre -1 et 1, nous prenons l'exemple de Q égal à 0,5. À chaque étape, nous prenons la moitié du terme précédent, et cela continue à l'infini. Nous comprenons intuitivement que lorsque nous prenons un nombre plus petit que 1, nous enlevons un petit bout à chaque fois, ce qui aboutit à 0. Si Q est égal à 1, tous les termes de la suite sont égaux à 1, donc cela converge vers 1. Si Q est inférieur à -1, la suite diverge, mais ne tend ni vers l'infini, ni vers moins l'infini. Nous illustrons ce cas avec Q égal à -0,7. Les termes de la suite oscillent mais convergent vers 0. En résumé, lorsque la raison Q est entre -1 et 1, la suite converge vers 0, soit en oscillant, soit pas. Lorsque la raison Q est supérieure à 1 ou inférieure à -1, la suite s'écarte de 0, soit vers l'infini, soit en s'écartant des deux côtés à la fois avec un terme sur deux. Cette vidéo donne une illustration visuelle de ces différents cas. La démonstration sera abordée dans une prochaine vidéo.

Suites géométriques : démo

Dans cette vidéo, nous allons démontrer les intuitions graphiques sur la limite des suites géométriques. Premièrement, si Q est strictement plus grand que 1, nous allons montrer que Q puissance n tend vers l'infini. Pour cela, nous utilisons l'inégalité de Bernoulli et le terrain de comparaison. Nous écrivons Q égal à 1 plus h, où h est positif. En utilisant l'inégalité de Bernoulli, nous obtenons que 1 plus h puissance n est plus grand ou égal que 1 plus n h. Comme 1 plus n h est une suite arithmétique de raison positive qui tend vers l'infini, nous pouvons conclure que Q puissance n tend vers l'infini. Ensuite, pour le cas où Q est entre 0 et 1, nous posons P égal à 1 sur Q. En appliquant le résultat précédent à P puissance n, nous obtenons que P puissance n tend vers l'infini. Comme Q puissance n est égal à 1 sur P puissance n, cela tend vers 1 sur l'infini, soit 0. Enfin, pour le dernier cas, nous utilisons le théorème des gendarmes. Nous posons s égal à moins Q, pour se rapporter au cas précédent. En utilisant le fait que s puissance n tend vers 0, nous pouvons encadrer Q puissance n entre moins s puissance n et s puissance n. Comme les deux encadrements convergent vers 0, nous pouvons conclure que Q puissance n tend également vers 0. En résumé, nous avons démontré les trois cas de la limite des suites géométriques. Le premier cas nécessite l'utilisation de l'inégalité de Bernoulli et constitue une démonstration plus approfondie. Les deux autres cas utilisent des astuces pour simplifier la démonstration. Il est important de connaître cette démonstration par cœur.

Limite avec A ou Ɛ

La vidéo traite de la définition formelle d'une limite mathématique en utilisant des exemples. L'objectif est de montrer comment ne pas avoir peur de cette définition et de la rendre compréhensible pour les étudiants qui continueront les mathématiques l'année suivante. L'exemple donné consiste à montrer que pour une suite donnée, Un=3n+2, il est possible de déterminer à partir de quel rang tous les termes de la suite sont supérieurs à un réel donné A. En traduisant la définition mathématique en français, on comprend que peu importe la hauteur du réel A, on veut montrer qu'à partir d'un certain rang n0, tous les termes de la suite dépassent cette hauteur. Pour résoudre l'équation 3n+2>A, on trouve que n>A-2/3. Puisque n doit être un entier naturel, on utilise la partie entière de A-2/3 plus 1, pour déterminer le plus petit entier n0 à partir duquel la propriété est vraie. La vidéo illustre également graphiquement cette idée, montrant que peu importe la hauteur de la barrière fixée (représentée par les réels A1, A2, A3), il existe toujours un rang à partir duquel tous les termes de la suite sont au-dessus de cette barrière. La définition formelle de la limite est ainsi présentée, soulignant que bien qu'elle puisse paraître complexe au début, elle devient plus simple à comprendre avec la pratique. La FAQ de la vidéo est également mentionnée pour toute question supplémentaire.