 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths SM&SP
Algèbre
2BAC SM Maroc

Automorphisme
Dans cette vidéo, Corentin parle de la notion d'automorphisme. Il explique qu'un automorphisme est une application qui va d'un groupe à lui-même. Pour déterminer les automorphismes de Z' plus (les entiers positifs), il faut trouver ceux qui sont injectifs et ceux qui sont surjectifs.
Corentin commence par rappeler ce qu'est un morphisme de groupe. Il explique que pour tout A et B dans Z (les entiers relatifs), f de A plus B est égal à f de A plus f de B, et f de 0 est égal à 0.
Ensuite, il démontre par récurrence que pour tout n dans N* (les entiers naturels non nuls), f de n est égal à n fois f de 1. Il montre également que pour les entiers négatifs, f de n est égal à n fois f de 1.
En conclusion, les morphismes de Z' plus dans Z' plus sont les fonctions qui vérifient f de n est égal à n fois f de 1, pour tout n dans Z.
Ensuite, Corentin se concentre sur les automorphismes surjectifs. Il propose de trouver une forme particulière et de vérifier si cette forme vérifie les conditions pour être un automorphisme surjectif. Il montre que f de 1 doit être égal à 1 ou -1 pour que f de Z soit égal à Z. Les morphismes surjectifs sont donc f de n est égal à n ou f de n est égal à -n.
Enfin, Corentin aborde les automorphismes injectifs. Il rappelle un théorème selon lequel un morphisme est injectif si et seulement si le noyau de ce morphisme est réduit à l'élément neutre du groupe. En appliquant ce théorème à Z' plus, il montre que tous les morphismes de Z' plus dans Z' plus sont injectifs, sauf l'application identiquement nulle.
En résumé, les automorphismes de Z' plus sont les fonctions qui vérifient f de n est égal à n fois f de 1, pour tout n dans Z. Parmi ces automorphismes, ceux qui sont surjectifs sont f de n est égal à n ou f de n est égal à -n, et ceux qui sont injectifs sont tous sauf l'application identiquement nulle.
Maths SM&SP
Algèbre
2BAC SM Maroc

Groupe Commutatif
Dans cette vidéo, Corentin explique la méthode pour montrer qu'un ensemble avec certaines lois est un corps commutatif. Il commence par rappeler la définition d'un corps et explique que pour prouver que cet ensemble est un corps, il faut vérifier plusieurs points.
La méthode 1, plus fastidieuse, consiste à appliquer la définition et à vérifier un à un les points de cette définition. Corentin montre notamment que l'addition est associative et commutative, que 0 est l'élément neutre et que tout élément a a un symétrique -a.
La méthode 2, plus rapide, consiste à montrer que l'ensemble est un sous-corps de R^3 en vérifiant que cet ensemble est stable par l'addition, la multiplication et l'inverse, et en montrant que 1 appartient à cet ensemble.
Corentin souligne l'importance de connaître la définition d'un corps, ainsi que l'utilisation du conjugué pour simplifier les calculs. Il rappelle également que pour prouver qu'un ensemble est un corps, il est souvent plus rapide de montrer qu'il est un sous-corps d'un autre ensemble.
En conclusion, il résume les points importants à retenir : connaître la définition d'un corps, utiliser le conjugué lorsque nécessaire et montrer que l'ensemble est un sous-corps pour simplifier la démonstration. Enfin, il remercie les spectateurs et termine la vidéo.
Maths SM&SP
Algèbre
2BAC SM Maroc

Groupe Symétrique
Dans cette vidéo, Corentin explique le concept d'un anneau de matrices et détermine les éléments inversibles de cet anneau.
Un anneau est un ensemble muni de deux opérations, l'addition et la multiplication, qui doivent satisfaire certaines propriétés. Corentin commence par rappeler la définition d'un anneau et d'un sous-anneau. Un sous-anneau est un sous-ensemble d'un anneau plus grand qui possède les mêmes opérations et satisfait les mêmes propriétés.
Ensuite, Corentin montre que l'ensemble A est un sous-anneau de M2 de R, c'est-à-dire l'ensemble des matrices 2x2 avec des coefficients réels. Il montre cela en effectuant des calculs pour l'addition et la multiplication de deux matrices quelconques de A. Il conclut que la matrice identité appartient également à A.
Enfin, Corentin aborde la deuxième question de déterminer les éléments inversibles de A. Il suppose l'existence d'une matrice inversible M et trouve son inverse M'. En utilisant les propriétés de l'égalité des matrices, il montre que M doit être égal à 1 ou à -1. Il conclut que les éléments inversibles de A sont ceux où M est égal à 1 ou à -1.
En résumé, cette vidéo explique le concept d'un anneau de matrices et détermine les éléments inversibles de cet anneau en effectuant des calculs et en utilisant les propriétés des matrices.
Maths SM&SP
Algèbre
2BAC SM Maroc

Etude de permutations
Dans cette vidéo, Corentin nous présente un exercice de mathématiques portant sur l'arithmétique et les structures algébriques. L'objectif est de démontrer qu'un certain ensemble, noté A, est un anneau, et de déterminer ses éléments inversibles.
Au départ, Corentin souhaite montrer rapidement que A est un sous-anneau de Q (les nombres rationnels). Pour cela, il considère deux éléments X et Y appartenant à A et calcule X - Y et X * Y. Il démontre que les dénominateurs de ces opérations sont impairs, ce qui montre que ces opérations sont stables dans A.
Ensuite, Corentin prouve que l'élément 1 appartient à A, car il peut être exprimé comme une fraction à dénominateur impair. Il conclut donc que A est bien un sous-anneau de Q, donc un anneau.
Enfin, Corentin s'intéresse aux éléments inversibles de A. Il considère un élément X appartenant à A et cherche son inverse Y. Il montre, en utilisant des calculs dans R (les nombres réels), que Y doit être égal à 1/X. La difficulté réside dans le fait de déterminer si cette inverse Y appartient toujours à A, qui est un ensemble de fractions à dénominateur impair.
Après quelques calculs, Corentin trouve la condition nécessaire pour qu'un élément X appartenant à A ait un inverse Y dans A : X doit être une fraction M/N, où M et N sont des nombres impairs.
Pour résumer, les éléments de A sont des fractions à dénominateur impair, ce qui en fait un sous-anneau de Q. Les éléments inversibles de A sont les fractions ayant un numérateur impair et un dénominateur impair, représentées par M/N où M et N sont des nombres impairs.
Maths SM&SP
Algèbre
2BAC SM Maroc

Anneaux, éléments nilpotents
Dans cette vidéo, Corentin aborde le concept de morphismes d'anneaux et démontre deux résultats. Tout d'abord, il montre que si K et L sont deux corps et F est un morphisme d'anneaux de K dans L, alors pour tout X appartenant à K privé de 0, F de X est inversible. Il explique ensuite comment déterminer l'inverse de F de X. Ensuite, Corentin souhaite montrer que tout morphisme de corps est injectif. Il rappelle une propriété selon laquelle un morphisme de corps est injectif si son noyau est réduit à 0. Il démontre alors que si F de X est égal à 0, alors X est égal à 0, ce qui montre que le noyau de F est réduit à 0 et donc que F est injectif.
Maths SM&SP
Algèbre
2BAC SM Maroc

Exemple d’anneau
Dans ce cours, Corentin explique comment démontrer qu'un ensemble Q n'admet pas d'autres sous-corps que lui-même. Pour cela, il utilise une double inclusion. Dans un premier temps, il montre que Q est inclus dans le sous-corps K en invoquant le fait que K est un sous-corps de Q, donc 0, 1 et tous les entiers naturels appartiennent à K. Il utilise également la stabilité de K par les opérations de plus et de passage à l'opposé pour montrer que l'ensemble des entiers relatifs est inclus dans K. Ensuite, en prenant un X appartenant à Q privé de 0, il démontre que ce X appartient à K en utilisant une écriture de X comme une fraction avec le numérateur P appartenant à Z et le dénominateur Q appartenant à N*. Puisque K est un corps, 1/Q appartient à K, ce qui implique que X appartient à K par stabilité par le produit. Ainsi, il montre que tous les éléments de Q privé de 0 appartiennent à K, en plus de 0 qui appartient déjà à K. Par conséquent, Q est inclus dans K. En combinant cette inclusion avec l'inclusion réciproque qui découle du fait que K est un sous-corps, on conclut que K est égal à Q. Ainsi, Q n'admet pas d'autres sous-corps que lui-même.
Maths SM&SP
Algèbre
2BAC SM Maroc

Anneaux d’entiers
Dans cette vidéo, Corentin discute d'un exercice mathématique portant sur un ensemble noté Z racine de 2. Il commence par expliquer l'énoncé de l'exercice, qui consiste à montrer que Z racine de 2, muni des opérations de l'addition et de la multiplication, forme un anneau.
Il explique ensuite qu'il est plus rapide et intuitif de montrer que Z racine de 2 est un sous-anneau de R plus, c'est-à-dire que les éléments de Z racine de 2 appartiennent à R plus et que les opérations de plus et de fois sont stables dans Z racine de 2. Il montre que Z racine de 2 vérifie ces conditions et conclut donc que c'est un anneau sous R plus.
Ensuite, il introduit une fonction n qui associe à chaque élément A plus B racine de 2 de Z racine de 2, la valeur A carré moins 2B carré. Il souhaite montrer que cette fonction est multiplicative, c'est-à-dire que n de xy est égal à n de x fois n de y pour tout x et y dans Z racine de 2. Il effectue le calcul correspondant et montre que cette égalité est vérifiée.
Enfin, il utilise cette fonction n pour trouver les éléments inversibles de Z racine de 2. Il explique sa méthode d'analyse synthèse, qui consiste à supposer qu'un élément x est inversible et à voir quelles conditions cela impose sur x. Il trouve que les éléments inversibles de Z racine de 2 sont ceux de la forme A plus B racine de 2 tels que A carré moins 2B carré est égal à plus ou moins 1.
Corentin conclut en résumant les étapes clés pour trouver les éléments inversibles de Z racine de 2 et en soulignant l'importance de vérifier que les éléments trouvés appartiennent bien à Z racine de 2.
Maths
Algèbre
MPSI/PCSI

Loi de composition
Aucun résumé n'est disponible pour cette vidéo
Maths
Algèbre
MPSI/PCSI

Sous groupes de R
Aucun résumé n'est disponible pour cette vidéo
Maths
Algèbre
MPSI/PCSI
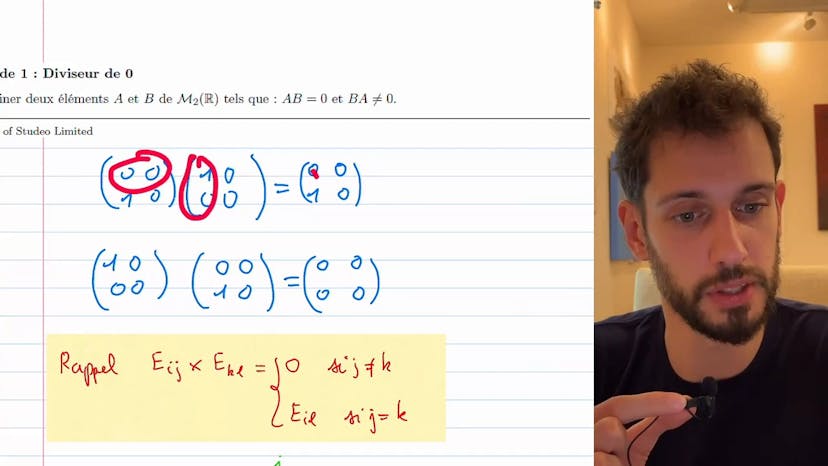
Diviseur de 0
Dans ce chapitre, nous abordons une méthode simple pour trouver des matrices et comprendre leur comportement. Nous devons trouver deux matrices de taille 2 dont le produit est égal à 0 dans un sens, mais pas dans l'autre sens. Cela souligne le fait que les matrices ne commutent pas nécessairement.
Lorsque nous recherchons des exemples de matrices, le plus simple est de commencer par des matrices fondamentales, qui sont des matrices avec des zéros partout sauf à un endroit. Nous les appelons Eij, où i représente la ligne et j la colonne. A cet endroit, nous plaçons un 1.
Une propriété intéressante de ces matrices est que le produit de Eij fois Ekl est toujours égal à 0, sauf lorsque la colonne de la première matrice rencontre la ligne de la deuxième matrice. Dans ce cas, nous avons une sorte de "choc" où Eijkl devient Eil lorsque j est égal à k.
Si nous prenons l'exemple des matrices de base M22R, nous pouvons voir que le produit de Eij fois Ekl est égal à Ekl. En revanche, le produit de Ekl fois Eij est égal à 0 car les 1 ne se rencontrent jamais.
Ainsi, cet exemple souligne l'importance d'utiliser des matrices simples avec beaucoup de zéros plutôt que de se compliquer la tâche. À la prochaine leçon !
Maths
Algèbre
MPSI/PCSI
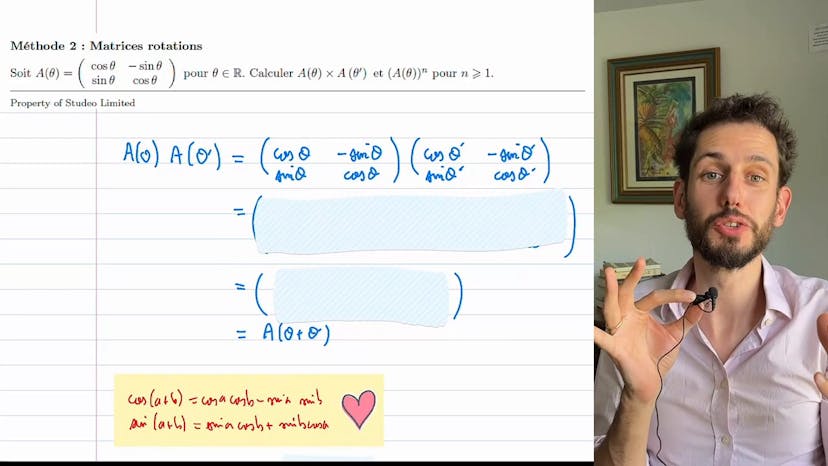
Matrices rotations
Dans cette vidéo, le cours porte sur le calcul avec des matrices, plus précisément sur une matrice appelée une matrice de rotation. Cette matrice relie les coordonnées cartésiennes aux coordonnées polaires en physique.
L'objectif est de calculer Aθ fois Aθ' et ensuite Aθ'. On remarque que lorsqu'on effectue une rotation de 30° puis de 50°, on obtient une rotation totale de 80°. On espère donc que le produit de rotation a une forme simple en fonction de θ et θ'.
Pour démontrer cela, on utilise une formule qui permet de reconnaitre certaines valeurs trigonométriques. En effectuant les remplacements nécessaires, on obtient A de θ plus θ'.
Ensuite, on souhaite obtenir A de θ puissance n. En utilisant à nouveau la formule avec A de θ plus θ, on obtient A de θ². Par récurrence, on peut alors écrire que A de θ puissance n est égal à A de nθ.
Il est important de bien comprendre ces concepts et d'effectuer les étapes de récurrence rapidement. Si vous avez des questions, n'hésitez pas à les poser. Au revoir et à bientôt pour une prochaine méthode.
Maths
Algèbre
MPSI/PCSI
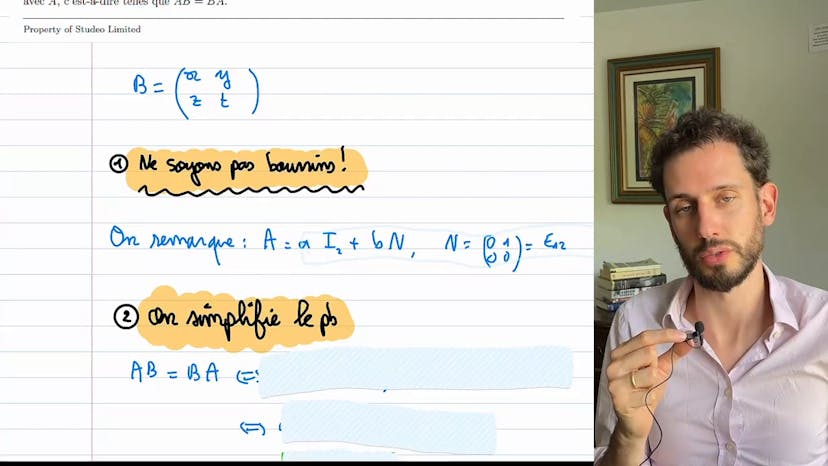
Commutant
Dans cet exercice, nous cherchons à trouver l'ensemble des matrices B qui commutent avec une matrice A donnée. Pour cela, nous observons que la matrice A peut être écrite comme la somme de deux matrices : A fois I2 (matrice identité) et B fois une matrice N (matrice triangulaire supérieure avec des 1 sur la diagonale). Cette matrice N est très utile et apparaît souvent dans ce type de problèmes.
En simplifiant le problème en utilisant cette écriture, nous obtenons AB = BA si et seulement si NB = BN. Cette équation plus simple nous permet de trouver une structure pour la matrice B : elle s'écrit sous la forme d'un réel fois I2 plus un réel fois N. Ainsi, l'ensemble des matrices qui commutent avec A peuvent également être écrites de cette manière.
Il est important de remarquer que cette méthode est plus efficace et rapide que d'autres approches plus lourdes pour résoudre ce type d'exercice. Il est également recommandé de retenir certaines matrices clés, comme la matrice N, qui apparaissent fréquemment et facilitent les calculs.
N'hésitez pas à poser des questions et restez à l'affût des prochaines vidéos.


