 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Algèbre
MPSI/PCSI
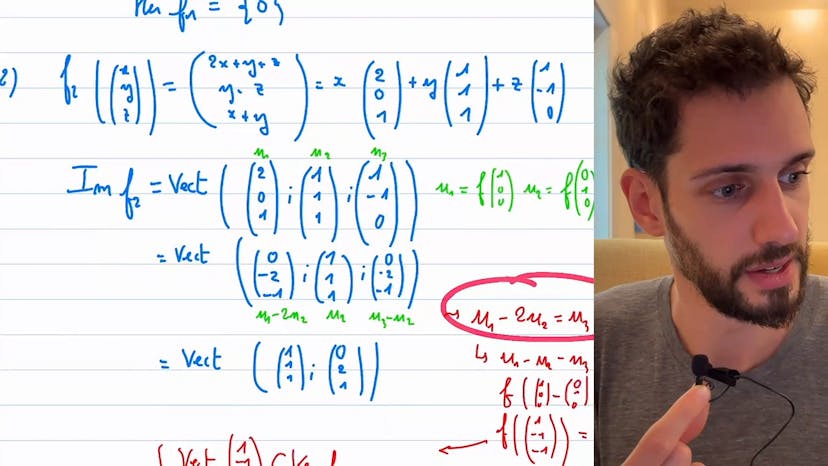
Injectivité et surjectivité
Dans cet exercice, nous étudions des applications linéaires avec des exemples concrets d'applications linéaires et nous déterminons les noyaux et les images de ces applications. Nous examinons chaque application pour déterminer si elle est injective, bijective ou surjective. En dimension finie, être injective, surjective ou bijective est complètement équivalent. Être injective signifie que le noyau est réduit à zéro. Être surjective signifie que l'image est égale à l'espace d'arrivée. Être bijective signifie que les deux sont vrais. En dimension infinie, cela peut être différent. Pour chaque fonction, nous analysons si elle est endomorphisme en restant dans R2 ou R3. Si les espaces de départ et d'arrivée sont différents ou si les dimensions sont différentes, cela ne sera pas un endomorphisme. En utilisant la technique de rédaction en colonne, nous pouvons déterminer l'image de chaque fonction. Nous utilisons des combinaisons linéaires pour trouver des vecteurs indépendants qui composent l'image. Nous utilisons également ces combinaisons linéaires pour trouver les vecteurs du noyau en utilisant une équation de la forme f(x) = 0. En comprenant les relations entre les vecteurs dans l'espace d'arrivée, nous pouvons déterminer les éléments du noyau.
Maths
Algèbre
MPSI/PCSI

Forme linéaire
Dans ce cours, nous étudions les formes linéaires, qui sont des applications linéaires avec un espace d'arrivée égal au corps de base. Nous devons montrer que toute forme linéaire non nulle est surjective. En d'autres termes, il faut montrer que pour chaque élément dans l'espace de départ, il existe au moins un élément correspondant dans l'espace d'arrivée.
Nous commençons par noter que l'image de la forme linéaire est incluse dans le corps de base. Puisque l'espace d'arrivée est petit, cela indique que le rang de la forme linéaire est inférieur ou égal à 1. Si le rang est égal à 0, cela signifie que la forme linéaire envoie tous les éléments sur 0, ce qui est l'application nulle, mais ce n'est pas le cas ici. Donc, le rang de la forme linéaire est égal à 1, ce qui nous permet de conclure que l'image de la forme linéaire est égale au corps de base, ce qui signifie que la fonction est surjective.
Ensuite, nous déduisons que le noyau d'une forme linéaire non nulle est un sous-espace vectoriel de dimension n-1. Cela est dû au théorème du rang, qui stipule que la somme des dimensions du noyau et de l'image est égale à la dimension de l'espace de départ. Par conséquent, la dimension du noyau est égale à la dimension de l'image, soit n-1.
Ensuite, nous nous intéressons à la réciproque. Nous prenons un sous-espace vectoriel H de dimension n-1 et vérifions s'il est possible de trouver une forme linéaire dont le noyau est H. Pour simplifier les choses, nous donnons une base à H, composée de n-1 vecteurs indépendants. En utilisant le théorème de la base incomplète, nous pouvons compléter H en ajoutant un élément U qui n'est pas dans H, de sorte que l'union de H et de U forme une base de l'espace de départ E. Ainsi, tout élément X de E peut être écrit comme une combinaison linéaire des vecteurs de H, plus une combinaison linéaire de U.
Ensuite, pour trouver une forme linéaire intéressante, nous définissons phi comme l'application qui prend un élément X de E et qui donne simplement sa coordonnée Xn sur le vecteur U. Cela signifie que tout élément de H sera envoyé sur 0. En résumé, pour un élément X appartenant à H, nous avons phi(X) = 0.
Enfin, nous montrons que si d'autres formes linéaires ont H comme noyau, elles seront parallèles à celle décrite précédemment, c'est-à-dire qu'elles seront de la forme lambda fois cette forme linéaire. Pour le prouver, nous utilisons à nouveau la décomposition de l'espace E en combinaison linéaire des vecteurs de H et de U. En appliquant une autre forme linéaire phi à un grand X exprimé de cette manière, nous pouvons séparer les termes correspondants à H et à U. Puisque les éléments correspondants à H sont dans le noyau de phi, leur image sera toujours égale à 0. Ensuite, nous remarquons que phi(U) est égal à lambda fois phi(X), où lambda est une constante. Ainsi, nous concluons que toute autre forme linéaire avec H comme noyau sera de la forme lambda phi(X).
Maths
Algèbre
MPSI/PCSI

Isomorphisme
Dans cet exercice, nous démontrons l'équivalence entre le fait que Phi soit un isomorphisme et le fait que l'image de toute base de E par Phi soit une base de F.
Nous commençons par montrer que si Phi est un isomorphisme, alors l'image de toute base de E par Phi est une base de F. Nous prenons une base E1 à Enne de E et vérifions si la famille Phi(E1) à Phi(Enne) est une base de F. Pour cela, nous effectuons un test de liberté en supposant que lambda1 à lambdan sont des constantes telles que la somme lambda1*Phi(E1) à lambdan*Phi(Enne) soit égale à 0. En utilisant la linéarité de Phi, nous déduisons que la somme lambda1*E1 à lambdan*Enne appartient au noyau de Phi. Cependant, le noyau de Phi étant réduit à 0, nous en concluons que les constantes lambda1 à lambdan doivent être nulles. Ainsi, la famille Phi(E1) à Phi(Enne) est libre et donc une base de F. Par conséquent, si Phi est un isomorphisme, alors l'image de toute base de E par Phi est une base de F.
Ensuite, nous démontrons que si l'image de toute base de E par Phi est une base de F, alors Phi est un isomorphisme. Nous prenons une base E1 à Enne de E et vérifions si la famille Phi(E1) à Phi(Enne) est une base de F. Si c'est le cas, alors dim F est égale à n qui est égale à dim E. En outre, puisque im(Phi) est égal à F par définition de la base, nous concluons que Phi est surjective. Ainsi, si l'image de toute base de E par Phi est une base de F, alors Phi est un isomorphisme.
En conclusion, nous avons démontré l'équivalence entre le fait que Phi soit un isomorphisme et le fait que l'image de toute base de E par Phi soit une base de F.
Prépa Examens
Concours et examens Français
Terminale

Une suite récurrente !
Dans cette vidéo, le professeur corrige le premier exercice du Tessia de 2022, qui concerne une suite récurrente. Il explique que cette suite est appelée une suite arithmético-géométrique et donne des conseils pour résoudre les questions. Il souligne l'importance de connaître les définitions des suites arithmétiques et géométriques pour pouvoir les exclure. Il propose également une astuce pour utiliser uniquement la différence entre deux termes consécutifs pour déterminer la nature de la suite. Ensuite, il explique comment trouver l'expression de la suite a_n et de la limite de u_n. Enfin, il termine en rédigeant une démonstration pour justifier la limite de u_n.
Prépa Examens
Concours et examens Français
Terminale

Identités algébriques !
Dans cette deuxième vidéo sur la correction du TESIA 2022, l'enseignant aborde l'exercice d'identité remarquable. Il mentionne également la date limite d'inscription pour le concours TESIA, soulignant son intérêt pour les participants potentiels.
L'exercice commence par des simplifications de calcul, où il faut mettre les termes au même dénominateur. Certaines parties sont plus complexes et nécessitent une attention particulière. L'enseignant conseille aux candidats de bien connaître les identités remarquables et de ne pas se précipiter. Il souligne l'importance de maîtriser les calculs pour réussir dans les études supérieures.
L'enseignant propose ensuite plusieurs méthodes pour résoudre une question plus difficile (M13) : trouver un cas particulier qui fonctionne pour une réponse donnée, effectuer des calculs avec des valeurs spécifiques, ou faire une démonstration plus approfondie en analysant chaque partie
Prépa Examens
Concours et examens Français
Terminale

Equations et inéquations !
Aucun résumé n'est disponible pour cette vidéo
Prépa Examens
Concours et examens Français
Terminale
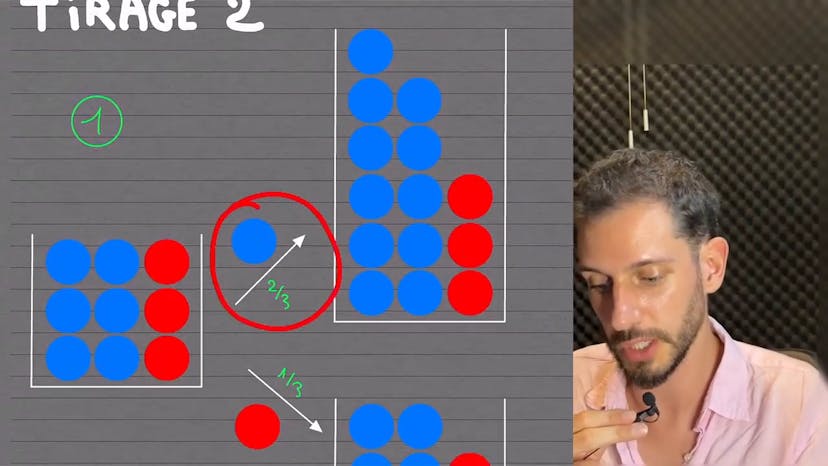
Des probabilités !
Dans ce cours, nous avons étudié un exercice sur les probabilités. Le premier conseil que l'enseignant donne est de faire un dessin complet avec un arbre de possibilités pour mieux comprendre la situation. Dans cet exercice, on nous indique qu'il y a une boule bleue et trois boules rouges. Si on tire une boule bleue, on la remet dans l'urne et on ajoute 5 boules bleues. Si on tire une boule rouge, on ne fait rien. Ensuite, on nous demande de faire un tirage numéro 2 selon les mêmes règles. Pour cela, on peut faire un arbre complet, mais faute d'espace, l'enseignant fait un dessin pour illustrer les différentes situations possibles. On peut ensuite résoudre les questions en se basant sur ce dessin. Par exemple, la probabilité d'obtenir une boule rouge au premier tirage est de 3/4. Si on suppose qu'on a tiré une boule bleue au premier tirage, la probabilité d'obtenir une boule bleue au deuxième tirage est de 5/12. On peut également calculer la probabilité d'obtenir deux boules bleues, une à chaque tirage, qui est de 1/6. Finalement, on nous demande de comparer la probabilité d'obtenir une boule bleue au deuxième tirage avec la probabilité d'obtenir une boule rouge. En utilisant les résultats précédents, on peut conclure que la probabilité d'obtenir une boule bleue au deuxième tirage est plus petite que la probabilité d'obtenir une boule rouge. Ensuite, nous abordons le cas d'une variable aléatoire X qui représente le nombre de boules bleues tirées dans l'expérience. On définit l'univers de cette variable comme étant {0, 1, 2}, c'est-à-dire qu'on peut obtenir 0, 1 ou 2 boules bleues. On calcule ensuite la probabilité d'obtenir X égal à 1 en utilisant les résultats précédents. On trouve que cette probabilité est de 1/3. Enfin, on nous demande de calculer l'espérance de la variable X. Pour cela, on utilise la formule de l'espérance qui consiste à multiplier chaque valeur possible de X par sa probabilité correspondante, puis à sommer le tout. On trouve que l'espérance de X est de 2/3. Voilà, en résumé, ce cours était une correction d'un exercice sur les probabilités avec différents calculs à faire en se basant sur un dessin représentant les différentes situations possibles.
Prépa Examens
Concours et examens Français
Terminale

Limites de fonctions !
Aucun résumé n'est disponible pour cette vidéo
Prépa Examens
Concours et examens Français
Terminale
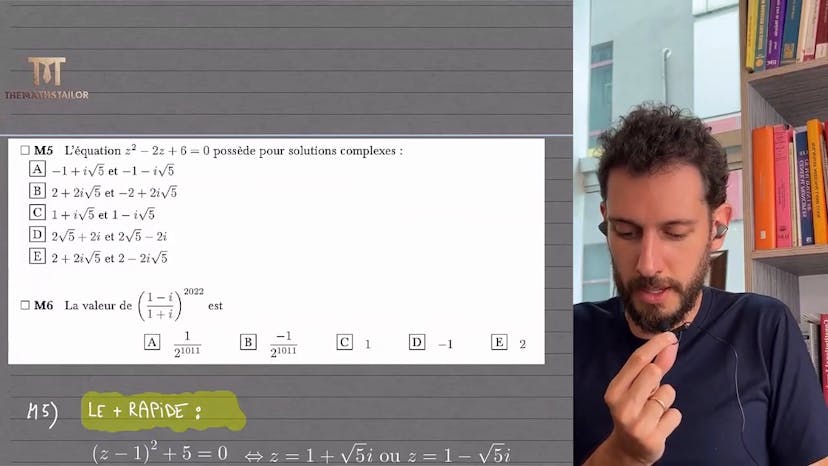
Nombres complexes en terminale
Aucun résumé n'est disponible pour cette vidéo
Prépa Examens
Concours et examens Français
Terminale

Nombres complexes et géométrie en terminale
Aucun résumé n'est disponible pour cette vidéo
Prépa Examens
Concours et examens Français
Terminale

Toutes les méthodes d'arithmétique
Aucun résumé n'est disponible pour cette vidéo
Prépa Examens
Concours et examens Français
Terminale
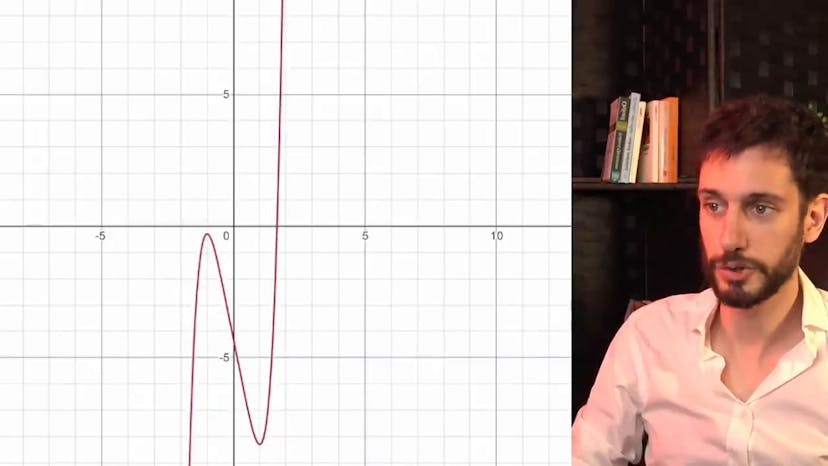
Solutions d'une équation de degré 5 !
Le cours aborde la résolution d'une équation de degré 5 qui consiste à trouver le nombre de solutions réelles en fonction d'un paramètre p. L'exercice nécessite une analyse approfondie de la fonction x^5 - 5x - p. Un graphe de la fonction est présenté pour illustrer les différentes valeurs de p et le nombre de solutions correspondant. En utilisant le théorème des valeurs intermédiaires, le professeur détermine différentes conditions pour le nombre de racines en fonction de la valeur de p. Il trouve qu'il y a une unique racine entre 1 et l'infini pour p>4, deux racines pour p=4, et trois racines pour -4<p<4. Pour p<-4, il y a à nouveau une unique racine. En résumé, l'ensemble des solutions de l'équation dépend de la valeur de p et peut être déterminé en analysant les différentes conditions. Le professeur encourage les étudiants à poser des questions et conclut en indiquant que d'autres exercices du même type seront présentés dans des vidéos futures.


