 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Prépa Examens
Concours et examens UK
Terminale
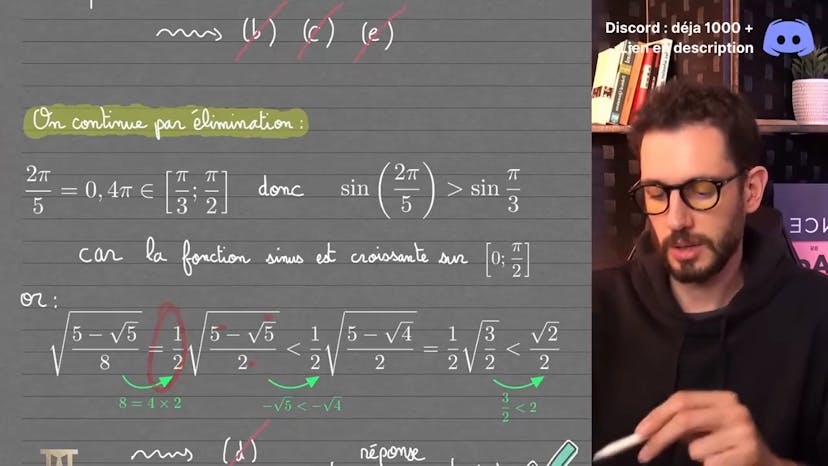
De la trigonométrie !
Ce cours est une transcription d'une vidéo qui explique une question de trigonométrie du Math Admission Test d'Oxford 2022. La question donne une relation sin5θ = 5sinθ - 20sinθ^3 + 16sinθ^5 et demande la valeur de sin72°. Le professeur utilise une méthode d'élimination pour trouver la réponse en commençant par éliminer les réponses qui donnent des valeurs négatives dans le quadrant où sin72° se trouve. Ensuite, il utilise la connaissance que sin72° est équivalent à 2π/5 pour éliminer les autres réponses et trouve que la réponse correcte est A. Il explique également une méthode plus longue qui utilise des équations polynomiales pour trouver la réponse, mais qui prend plus de temps. Il conseille de rester concentré sur les informations données dans la question et de ne pas s'égarer sur des méthodes plus complexes.
Maths
Probabilités
MPSI/PCSI
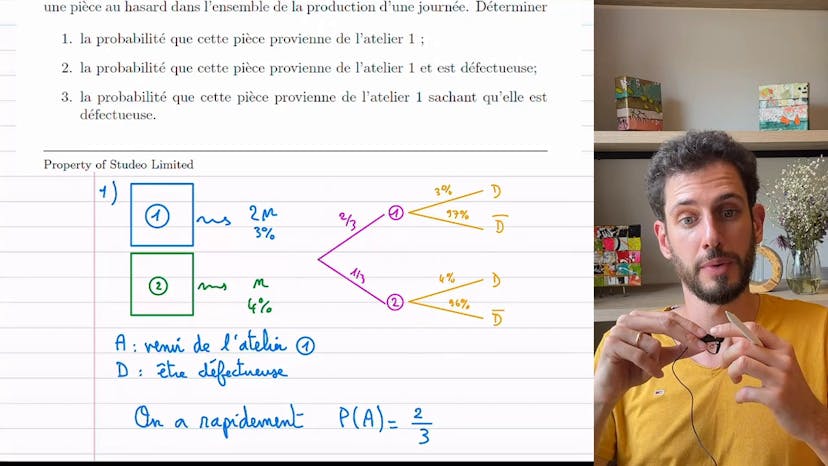
Deux ateliers
L'exercice consiste à analyser deux ateliers d'une entreprise qui fabriquent des pièces. L'atelier 1 produit deux fois plus de pièces que l'atelier 2, mais l'atelier 2 a un pourcentage de pièces défectueuses plus élevé (4% contre 3% pour l'atelier 1).
Pour mieux comprendre la situation, il est recommandé de faire un dessin représentant les probabilités. En utilisant cet arbre, on constate que sur 3N pièces, 2N viennent de l'atelier 1, ce qui signifie que la probabilité de prélever une pièce de l'atelier 1 est de 2/3.
Ensuite, on aborde les différentes questions. La probabilité que la pièce provienne de l'atelier 1 ET soit défectueuse est calculée en utilisant la formule du cours : P(D inter A) = P(D|A) * P(A). Dans ce cas, la probabilité est de 2%.
Pour la troisième question, qui demande la probabilité que la pièce provienne de l'atelier 1 sachant qu'elle est défectueuse, on utilise la formule de Bayes. On calcule d'abord la probabilité d'avoir une pièce défectueuse en utilisant la formule des probabilités totales. On obtient ainsi une probabilité de 10/3, soit environ 3,33%. En utilisant cette information, on peut ensuite calculer la probabilité recherchée (P(A|D)), qui est de 60%.
En conclusion, il est important de bien retenir ces formules, de faire un dessin pour représenter la situation et de poser des questions si nécessaire.
Maths
Probabilités
MPSI/PCSI
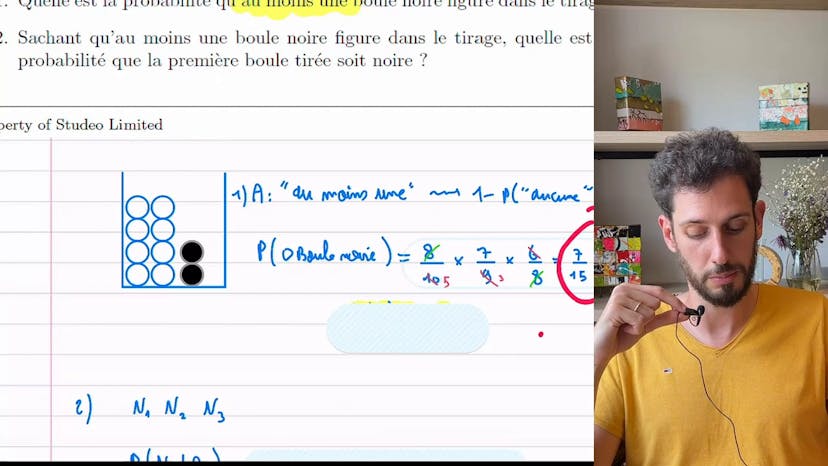
À partir de dénombrement
Ce cours présente un problème de probabilité concernant le tirage de boules d'une urne. Dans cette urne, il y a 8 boules blanches et 2 boules noires. On effectue 100 tirages successifs de 3 boules. L'objectif est de calculer la probabilité d'avoir au moins une boule noire dans le tirage.
Pour résoudre ce problème, on commence par calculer la probabilité d'avoir zéro boule noire dans le tirage. Pour cela, on multiplie la probabilité d'avoir une boule blanche lors du premier tirage (8/10) par la probabilité d'avoir une autre boule blanche lors du deuxième tirage (7/9), puis par la probabilité d'avoir une troisième boule blanche lors du troisième tirage (6/8). On obtient ainsi une probabilité de 7/15.
La probabilité d'avoir au moins une boule noire est donc égale à 1 - 7/15, ce qui donne 8/15.
Ensuite, on s'intéresse à la probabilité que la première boule tirée soit noire, sachant qu'au moins une boule noire figure dans le tirage. On utilise la formule de Bayes pour calculer cette probabilité conditionnelle. On obtient finalement une probabilité de 3/8.
Ceci résume le cours de manière SEO friendly, en mettant en évidence les mots clés importants du sujet, à savoir : tirage, boules, probabilité, au moins une, urne.
Maths
Probabilités
MPSI/PCSI

Formule de Bayes
On a un gérant de magasin d'informatique qui a reçu un lot de clés USB. 5% des boîtes sont abîmées. Le gérant estime que 60% des boîtes abîmées contiennent au moins une clé défectueuse. 98% des boîtes non abîmées ne contiennent aucune clé défectueuse. Un client achète une boîte du lot. On cherche à calculer les probabilités suivantes : P(A), P(~A), P(D|A), P(D|~A), P(~D|A), P(~D|~A), et P(D). En utilisant la formule des probabilités totales, on obtient P(D) = 4,9%. Si un client constate qu'une clé achetée est défectueuse, la probabilité qu'il ait acheté une boîte abîmée est de 61,2%. Il y a donc 40% de chances qu'une clé défectueuse provienne d'une boîte non abîmée.
Maths
Probabilités
MPSI/PCSI

Questionnaire de Bayes
Dans cette vidéo, on aborde un problème de probabilités lié à un QCM de mathématiques. Le contexte est un peu drôle car il s'agit de déterminer la probabilité qu'un étudiant qui a répondu correctement connaissait réellement la réponse.
On pose donc plusieurs événements : C pour "l'étudiant connaît la réponse" et J pour "l'étudiant a eu juste". On utilise ensuite la formule des probabilités conditionnelles pour calculer la probabilité que l'étudiant connaisse la réponse en fonction de la probabilité qu'il ait juste.
Si l'étudiant connaît la réponse (événement C), alors la probabilité d'avoir juste est de P (où P est la probabilité qu'un étudiant connaisse la réponse). Si l'étudiant ne connaît pas la réponse, il a une chance sur M (le nombre de réponses possibles) d'avoir juste.
Pour calculer la probabilité que l'étudiant connaisse la réponse sachant qu'il a eu juste (événement C sachant J), on utilise la formule des probabilités conditionnelles. On obtient alors P de C sachant J = P / (MP / (1 + MP - P(1/M)).
Cet exercice permet de mettre en évidence les liens entre les différentes probabilités et d'utiliser des formules mathématiques pour les calculs.
Maths
Probabilités
MPSI/PCSI

Dés pipés
Dans cet exercice de probabilités intéressant, nous avons 100 dés, parmi lesquels 25 sont pipés et permettent de gagner plus facilement. Chaque dé pipé a une probabilité de 1,5 d'obtenir un 6, tandis que les autres dés ont une probabilité de 1/6.
Lorsque nous tirons un dé au hasard et obtenons un 6, nous voulons savoir quelle est la probabilité que le dé soit pipé. Pour cela, nous utilisons l'arbre des probabilités et utilisons les notations suivantes : P pour le dé pipé, et 6 pour obtenir un 6.
Nous avons 1 chance sur 4 (25 sur 100) d'obtenir un dé pipé, et donc 3 chances sur 4 d'obtenir un dé non pipé. En ce qui concerne les probabilités d'obtenir un 6, pour les dés pipés, c'est 1,5, et pour les dés non pipés, c'est 1/6.
Maintenant, nous voulons calculer la probabilité d'avoir un dé pipé sachant que nous avons obtenu un 6. Pour cela, nous utilisons la formule de la probabilité conditionnelle en utilisant les probabilités intermédiaires : P(inter 6) = 1,25 x 1,5, et P(6) = P(inter 6) + P(inter 6 complémentaire) = 1,25 + 3,25 x 1,5. En simplifiant, nous obtenons une probabilité finale de 1,25.
Ainsi, lorsque nous obtenons un 6, la probabilité que le dé soit pipé est de 1,25, soit 1 chance sur 2.
Maintenant, nous passons à un scénario plus complexe. Supposons que nous tirions un dé au hasard parmi les 100 dés et que nous le lancions n fois, obtenant chaque fois un 6. Nous voulons maintenant calculer la probabilité que le dé soit pipé.
Dans ce cas, nous avons toujours 1/4 de chance d'obtenir un dé pipé et 3/4 de chance d'obtenir un dé non pipé. Pour les dés pipés, la probabilité d'obtenir un 6 n fois est de 1,5^n, tandis que pour les dés non pipés, elle est de (1/6)^n.
Pour calculer la probabilité que le dé soit pipé sachant que nous avons obtenu un 6 n fois, nous utilisons la formule de Bayes. Nous obtenons P(n) = (1/2)^n / [(1/4)(1/2)^n + (3/4)(1/6)^n].
En simplifiant cette expression, nous arrivons à P(n) = 1 / (1 + (3/2)^n). Il est important de noter que cette probabilité diminue à mesure que le nombre de fois où nous obtenons un 6 augmente.
En fin de compte, si nous avons obtenu un 6 n fois, la probabilité que le dé soit pipé tend vers 0, ce qui signifie qu'il est très peu probable que le dé soit pipé dans ce scénario.
Maths
Analyse
MPSI/PCSI

Théorème de Darboux
Dans ce cours, nous avons examiné une méthode pour démontrer le théorème de Darboux, qui est une extension du théorème des valeurs intermédiaires. Nous avons d'abord noté qu'il n'est pas trivial de prouver ce théorème, car la fonction dérivée n'est pas nécessairement continue. Ensuite, nous avons supposé que f'(A) est inférieur à f'(B), avec un réel Z compris entre les deux. Nous avons ensuite utilisé la notion de limite pour construire notre raisonnement. Nous avons montré que si une fonction est dérivable en A, alors le taux d'accroissement tend vers f'(A). En utilisant cette propriété, nous avons trouvé un epsilon qui nous permet de prouver que Z est compris entre les taux d'accroissement en A et B. Ensuite, nous avons montré qu'il existe un point Y tel que le taux d'accroissement en ce point soit égal à Z. Enfin, nous avons utilisé le théorème des accroissements finis pour montrer que Z appartient à l'intervalle des taux d'accroissement en Y. En résumé, nous avons montré que si f'(A) est inférieur à f'(B), alors tout réel Z appartenant à l'intervalle de f'(A) à f'(B) appartient à f'(Y), où Y est un point compris entre A et B. Nous avons appliqué cette méthode à une fonction spécifique, x²sin(1/x²), pour montrer que f est dérivable mais que f' n'est pas continue sur l'intervalle ouvert (0,1).
Maths
Analyse
MPSI/PCSI

Théorème du point fixe
Bonjour à tous ! Aujourd'hui, nous allons parler du point fixe en mathématiques, plus précisément des points attractifs. Nous avons une fonction f qui est dérivable sur l'intervalle [a, b], et nous supposons qu'il existe une constante k appartenant à [0, 1] telle que la dérivée de f soit inférieure en valeur absolue à k. Un point fixe est une solution gamma telle que f(gamma) = gamma.
Tout d'abord, nous montrons que ce point fixe est unique. Pour cela, nous posons g(x) = f(x) - x et utilisons le théorème des valeurs intermédiaires (TVI) pour montrer qu'il existe au moins un point fixe. Ensuite, nous supposons qu'il y en a deux et utilisons le théorème des inégalités des accroissements finis (IAF) pour montrer qu'ils sont identiques.
Ensuite, nous considérons une suite définie par récurrence et souhaitons montrer qu'elle converge vers le point fixe gamma. Pour cela, nous utilisons à nouveau l'IAF pour encadrer u(n) - gamma et démontrer que cette suite converge vers 0, ce qui implique que u(n) converge vers gamma.
En conclusion, nous avons vu que le point fixe est unique, qu'il est attractif et comment utiliser le théorème du point fixe dans des exercices.
Maths
Analyse
MPSI/PCSI
Somme sinusoïdale
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Physique
MPSI/PCSI

Moment cinétique d'un point de masse M
Dans cette vidéo, nous étudions le moment cinétique d'un point M se déplaçant en trajectoire circulaire autour d'un point O. Le point M possède une masse M et se déplace selon des coordonnées cylindriques. Le but de l'exercice est de calculer le moment cinétique Lz par rapport à l'axe OZ.
Pour cela, nous commençons par faire un schéma de la situation, en représentant les vecteurs Uz, Ur et Uteta. Le point M se trouve à une distance R du centre O. Le moment cinétique d'un point M est le produit vectoriel de son vecteur position OM et de son vecteur vitesse MV. En substituant les valeurs, nous obtenons L = MR²θ.Uz.
Cependant, nous cherchons le moment cinétique par rapport à l'axe OZ. En observant le schéma, nous remarquons que Uz et L sont tous les deux parallèles à OZ. Cela signifie que toutes les composantes du moment cinétique sont alignées avec OZ. Par conséquent, le produit scalaire entre L et Uz est égal à la norme de L.
Ainsi, le moment cinétique par rapport à l'axe OZ du point M est égal à MR²θ.Uz. Ce résumé permet de poser les bases avant de passer à la suite du cours. Si vous avez des questions, n'hésitez pas à les poser. Merci.
Physique-Chimie
Physique
MPSI/PCSI
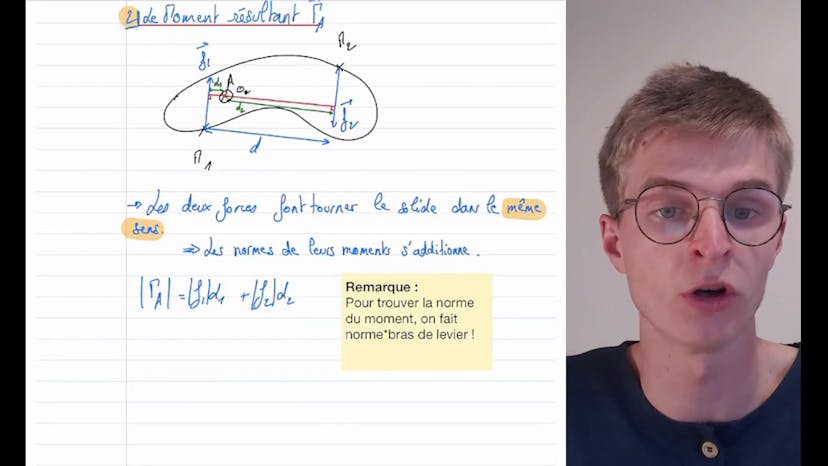
Couple de deux forces opposées
Dans cette vidéo, nous abordons le sujet des couples de forces appliquées à un solide indéformable. Un solide indéformable est soumis à deux forces opposées, F1 et F2, avec F1 étant inférieur à F2. F1 est appliquée au point M1 et F2 au point M2 du solide. Nous prenons un point A fixe sur le solide et calculons la force résultante F par rapport à A et le moment résultant gamma A par rapport à A.
Pour calculer la force résultante F, nous effectuons un bilan des forces. Comme les forces F1 et F2 sont opposées, leur somme vectorielle donne 0. Par conséquent, la résultante par rapport à A est nulle.
Le moment résultant gamma A est intéressant à examiner dans cet exercice. Les deux forces F1 et F2 contribuent à faire tourner le solide dans le même sens. Leurs moments respectifs s'additionnent, donnant gamma A égal à la norme du moment de F1 plus la norme du moment de F2. Pour calculer la norme d'un moment, il faut multiplier la norme de la force par le bras de levier correspondant. Par conséquent, gamma A est égal à F1 fois D plus F2 fois D, où D est la distance entre les points d'application des forces.
Le moment résultant gamma A s'applique dans le plan orthogonal à OZ, dans lequel le solide est placé. Étant donné que le solide tourne dans le sens direct et que OZ rentre à l'intérieur de ce plan, le moment participe à faire tourner le solide dans le sens direct. Ainsi, le moment par rapport à A est égal à la norme de F1 fois D, avec une orientation selon UZ. Ce type de situation, où deux forces opposées avec la même norme contribuent à faire tourner le solide dans le même sens, est appelé un couple. Par conséquent, le couple dans cet exercice est représenté par F1 fois D fois UZ.
C'est la fin de cet exercice. N'hésitez pas à poser des questions dans les commentaires et rejoignez-nous pour le prochain exercice.
Physique-Chimie
Physique
MPSI/PCSI

Mouvement d'un pendule pesant
Dans cette vidéo, Théobald de Studio explique un exercice sur le pendule pesant. Le pendule est attaché au point O et oscille autour de l'axe OZ. On note J son moment d'inertie, G son centre de gravité, et D la distance OG.
La première question demande de faire la liste des actions mécaniques appliquées sur le pendule et de calculer leur résultant et leur moment par rapport à l'axe OZ. Théobald explique que le poids du solide est P = -MGUY, car G et UY sont opposés. Le moment du poids est alors -MGDsinθUZ, car le poids tend à faire tourner le solide selon Uθ. En ce qui concerne la liaison pivot, son moment par rapport à l'axe Z est nul, et la force de la liaison pivot n'est pas encore déterminée. Ainsi, la force résultante est la somme du poids et de la force de la liaison pivot, et le moment résultant est -MGDsinθ.
Dans la deuxième question, il est demandé d'appliquer le théorème du moment cinétique pour déterminer l'équation différentielle du mouvement. Théobald explique que le théorème du moment cinétique s'applique par rapport à un axe fixe OZ. La dérivée du moment cinétique par rapport au temps est égale au moment résultant. L'équation du mouvement s'obtient donc en substituant les valeurs connues : θ + MGDsinθ/J * sinθ = 0.
La troisième question demande s'il est possible de retrouver cette équation en appliquant le théorème de la résultante cinétique. Théobald explique que le théorème de la résultante cinétique est essentiellement un PFD et fournit des informations sur les forces extérieures. Bien que l'on puisse obtenir des informations sur la force de la liaison pivot, il n'est pas possible de retrouver directement l'équation du mouvement en utilisant ce théorème. Cependant, en utilisant l'équation du mouvement, on peut déduire des informations sur la force de la liaison pivot, qui vaut MA-MG.
Le cours se termine avec une invitation à poser des questions dans les commentaires et une promesse de nouvelles vidéos à venir.


