Cours d'apprentissage en ligne

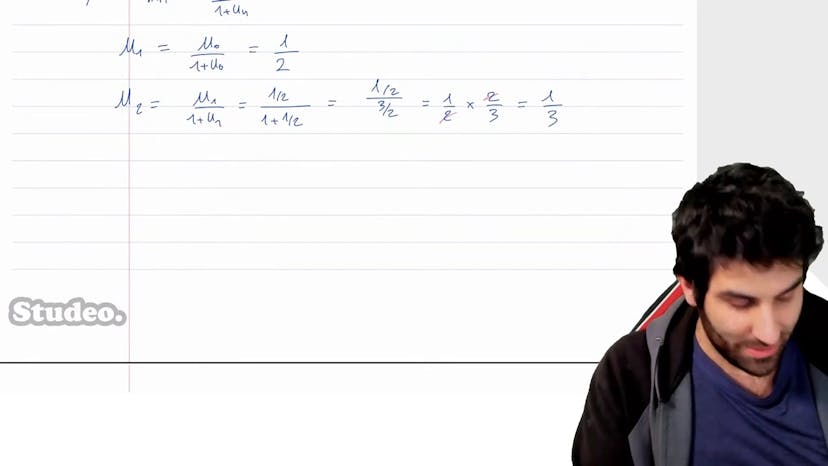
Suites - Polynésie 2022

Aucun résumé n'est disponible pour cette vidéo

Dans cet exercice, nous étudions les probabilités liées à une maladie et à un test de dépistage. Le contexte se base sur l'hypothèse de 7% de la population touchée par cette maladie. Le test de dépistage donne des faux négatifs dans 20% des cas pour les personnes malades, et des faux positifs dans 1% des cas pour les personnes non malades. Les questions posées portent notamment sur la probabilité d'être malade et d'avoir un test positif, la fiabilité du test, ainsi que le nombre minimum de personnes à tester pour qu'au moins l'une d'entre elles ait un test positif avec une probabilité supérieure à 99%. Les probabilités sont calculées en utilisant des arbres pondérés, des formules de probabilités conditionnelles et la loi binomiale. En conclusion, il est recommandé de privilégier la connaissance de la probabilité d'être malade sachant que le test est positif, dans un contexte de dépistage de maladie. Enfin, il est nécessaire de tester au moins 69 personnes pour avoir une probabilité supérieure à 99% qu'au moins l'une d'entre elles ait un test positif.

Géométrie - Polynésie 2022

Aucun résumé n'est disponible pour cette vidéo

Fonctions - Asie 2022

Aucun résumé n'est disponible pour cette vidéo

Probabilités - Asie 2022

Cet exercice porte sur les probabilités, les probabilités conditionnelles, les indépendances et les variables aléatoires. La première partie concerne les événements et les prob

Suites - Asie 2022

Dans cet exercice de BAC sur les suites avec de l'algorithmique et de la programmation, on étudie le développement d'une bactérie en utilisant des probabilités. On modélise le développement de la bactérie avec certaines hypothèses : elle a une probabilité de 0,3 de mourir sans descendance et une probabilité de 0,7 de se diviser en deux bactéries. On utilise la relation de récurrence P_n+1 = 0,3 + 0,7 * P_n^2 pour calculer les valeurs de P_1 et P_2. On obtient P_1 = 0,363 et P_2 = 0,3922383. Ces valeurs indiquent que la bactérie a plus de chances d'avoir au moins 1 ou 2 descendants que 0. Ensuite, on nous demande de déterminer la probabilité, arrondie à 10^-3, d'obtenir au moins 11 générations de bactéries à partir d'une bactérie de ce type. On utilise la relation P_n <= 0,5 pour montrer que P_10 est l'inégalité exacte. Donc, la probabilité d'obtenir au moins 11 générations est égale à 1 - P_10, soit environ 0,571. On formule ensuite des conjectures sur les variations et la convergence de la suite P_n. En observant le tableau, on voit que les termes de la suite semblent converger vers 0,428, en étant croissants. On conclut que la suite est croissante et convergente. Par récurrence sur n, on démontre que pour tout entier naturel n, P_n < P_n+1 et les deux sont compris entre 0 et 0,5. On justifie ensuite que la suite est convergente en montrant que P_n < P_n+1, ce qui prouve que la suite est croissante, et que tous les termes de la suite sont inférieurs à 0,5. On détermine alors la limite de la suite en résolvant l'équation 0,3 + 0,7 * l^2 = l, où l est la limite de la suite. On trouve l = 3/7, soit environ 0,430. Enfin, on écrit une fonction en Python qui renvoie les n premiers termes de la suite. On initialise le tableau avec la valeur de P_0, puis on utilise une boucle pour calculer les termes suivants en utilisant la relation de récurrence. On ajoute chaque terme calculé au tableau avec la fonction append, et on renvoie le tableau complet. Cet exercice permet de mettre en pratique les concepts de suites, probabilités et programmation, en étudiant le développement d'une bactérie avec des hypothèses et des calculs de probabilités. On calcule les valeurs de la suite, interprétons les résultats dans le contexte, démontrons des propriétés sur la

Fonctions - Nouvelle Calédonie 2022

Cet exercice porte sur l'étude des fonctions, des fonctions logarithmes et de la convexité. Il comporte plusieurs questions classiques telles que le calcul de limite, la dérivation, le tableau de variations et le théorème des valeurs intermédiaires. La question qui se démarque concerne la position relative d'un segment par rapport à la courbe d'une fonction. Dans la première partie, on calcule la limite de la fonction f(x) en 0. On sépare la fonction en polynôme et logarithme et on obtient que f(x) tend vers moins l'infini. Cela indique la présence d'une asymptote verticale à la courbe de f(x) pour x = 0. Ensuite, on détermine la limite de f(x) quand x tend vers plus l'infini. On factorise la fonction et on constate que f(x) tend vers plus l'infini. On détermine ensuite la dérivée de f(x) et on étudie le signe de cette dérivée. On trouve que f(x) est croissante sur l'intervalle 0 à √2 et décroissante sur l'intervalle √2 à plus l'infini. On montre ensuite que l'équation f(x) = 0 admet une unique solution dans l'intervalle [4, 5] en utilisant le théorème des valeurs intermédiaires. On admet la dérivée seconde et on étudie la convexité de la fonction f(x). On trouve que f(x) est concave sur l'intervalle [0, √2] et convexe sur l'intervalle [√2, +∞]. Enfin, on utilise les informations précédentes pour déterminer la position relative du segment AM (corde) par rapport à la courbe de f(x). Si le point M est compris entre 0 et √2, le segment AM est en dessous de la courbe. Si le point M est compris entre √2 et plus l'infini, le segment AM est au-dessus de la courbe. Cet exercice permet de mettre en pratique plusieurs concepts importants en étude de fonctions et en calcul de limites, tout en abordant un problème un peu plus original concernant la position relative d'un segment par rapport à une courbe.

Suites et fonctions - Nouvelle Calédonie 2022

Dans cet exercice, nous étudions la fonction exponentielle et une suite définie par récurrence. Tout d'abord, nous calculons les premiers termes de la suite, u1 et u2, en utilisant la fonction f définie par f(x) = x^3 * e^x. Ensuite, nous démontrons par dérivation que pour tout x réel, f'(x) = x^2 * e^x * (x+3). En utilisant les variations de cette fonction, nous justifions le tableau de variation de f. Enfin, nous démontrons par récurrence que pour tout entier naturel n, -1 ≤ un ≤ 0. Pour cela, nous montrons que la proposition est vraie au rang 0, et nous supposons qu'elle soit vraie au rang n pour montrer qu'elle est vraie au rang n+1. En utilisant cette propriété, nous déduisons que la suite un est croissante et majorée par 0, et donc elle converge vers un réel l ≤ 0. En résolvant l'équation f(x) = x, nous trouvons que l est nécessairement égal à 0. Ainsi, nous avons déterminé la limite de la suite un.

Géométrie - Nouvelle Calédonie 2022

Dans cet exercice de géométrie dans l'espace, nous avons un cube avec un repère et différents vecteurs exprimés en fonction des vecteurs AB, AD et AE. Le but est de déterminer les coordonnées d'un point, montrer qu'un vecteur est normal à un plan, donner une équation cartésienne du plan et une représentation paramétrique d'une droite. D'abord, nous devons trouver les coordonnées du point G en exprimant le vecteur AG en fonction des vecteurs de base. En utilisant les relations données, on trouve que les coordonnées de G sont 3, 2 et 1. Ensuite, nous devons montrer que le vecteur N de coordonnées 2, 0 et -3 est normal au plan EHI et déterminer une équation cartésienne de ce plan. En utilisant les coordonnées du vecteur, nous écrivons une équation cartésienne de la forme 2X + 0Y - 3Z + D = 0 et trouvons que D = 3. L'équation cartésienne de EHI est donc 2X - 3Z + 3 = 0. Nous devons également trouver les coordonnées du point I en utilisant le fait que le triangle EIF est isocèle en I. Nous trouvons que les coordonnées de I sont 3.5, 0 et 2. Ensuite, nous devons mesurer l'angle EIF avec précision. En utilisant le produit scalaire, nous calculons le cosinus de l'angle et trouvons qu'il est égal à -5/13. En utilisant la fonction arc cosinus, nous trouvons que l'angle EIF est d'environ 112.6 degrés. Enfin, nous devons donner une représentation paramétrique de la droite delta qui passe par le point R de coordonnées 6, -3, -1 et est dirigée par le vecteur U de coordonnées -3, 4, 1. La représentation paramétrique de delta est donc X = 6 - 3T, Y = -3 + 4T, Z = -1 + T. Pour déterminer les coordonnées du point K, intersection de la droite delta et du plan BFG, nous utilisons la représentation paramétrique de delta en égalant X à 3. En trouvant la valeur de T qui vérifie cela, nous trouvons que les coordonnées de K sont 3, 1, 0. Finalement, nous vérifions que le point K appartient bien à la rète BC en utilisant une équation de droite ou en remarquant que les coordonnées de K sont les demi-sommes des coordonnées de B et C, indiquant que K est le milieu de BC et donc appartient au segment BC.

Suites et fonctions - Centres étrangers 2022

Cours sur les exponentiels et les suites: la partie exponentielle consiste en l'étude de fonctions. Nous examinons les limites en l'infini, en moins l'infini, zéro ou un certain nombre. Nous devons faire un tableau de variation, montrer des inégalités et résoudre des équations de tangente. Il y a également des limites de suite à examiner et des variations de suite à déterminer. Tout cela est nécessaire pour réussir l'examen du BAC. Dans la première partie de l'exercice, nous devons déterminer les limites de la fonction h(x) = e^x - x lorsque x tend vers plus l'infini et moins l'infini. En utilisant la méthode de factorisation, nous trouvons que la limite de h(x) en plus l'infini est plus l'infini et la limite de h(x) en moins l'infini est moins l'infini. Ensuite, nous devons étudier les variations de h et dresser son tableau de variation. En dérivant la fonction, nous trouvons que sa dérivée est positive lorsque x est positif et négative lorsque x est négatif. En utilisant ces informations, nous dressons le tableau de variation de h. La partie suivante concerne l'équation de la tangente à la courbe d'une fonction f au point d'abscisse 0. En utilisant les dérivées de f, nous déterminons que l'équation de la tangente est y = x + 1. Enfin, nous abordons la suite un = e^(1/n) - 1/n - 1 et déterminons sa limite qui est de 0. Nous devons ensuite démontrer que pour tout entier naturel non nul n, un+1 - un = h(1/(n+1)) - h(1/n). En utilisant les propriétés de h, nous montrons que cette égalité est vraie. Pour la dernière partie de l'exercice, nous utilisons un tableau de valeurs pour déterminer la plus petite valeur de l'entier naturel pour laquelle l'écart entre la tangente et la courbe de f est inférieur à 0,01. En regardant le tableau, nous trouvons que lorsque n est égal à 8, l'écart est inférieur à 0,01. En résumé, cet exercice porte sur les exponentiels et les suites. Nous devons déterminer des limites, étudier les variations de fonctions, résoudre des équations de tangente et examiner les variations de suites.

Probabilités - Centres étrangers 2022

Cet exercice porte sur les probabilités et concerne la fabrication de paires de lunettes. Il y a deux traitements, T1 et T2, pour lesquels on souhaite calculer les probabilités de présence de défauts. On utilise les probabilités conditionnelles, l'indépendance, la loi binomiale, ainsi que la formule des probabilités totales. Le tableau fourni présente les probabilités de présence de défauts pour chaque traitement, ainsi que la probabilité qu'aucune des deux paires ne présente de défaut. On peut remplir le reste du tableau en utilisant les sommes de probabilités. On peut ensuite calculer la probabilité qu'une paire de verres présente au moins un défaut pour l'un des traitements en utilisant la formule de l'union. On trouve ainsi une probabilité de 0,25. La probabilité d'avoir deux défauts pour chaque traitement correspond à la probabilité d'intersection, et est égale à 0,05. Les événements A et B ne sont pas indépendants car le produit de leurs probabilités n'est pas égal à la probabilité de leur intersection. La probabilité d'avoir exactement un défaut pour un seul des traitements correspond à la probabilité de l'union moins la probabilité de l'intersection. On trouve une probabilité de 0,2. La probabilité d'avoir un défaut pour le traitement T2 sachant qu'il y a un défaut pour le traitement T1 est égale à 0,5. Dans la partie B de l'exercice, on considère un échantillon de 50 paires de verres. On déclare une variable aléatoire X qui représente le nombre de paires de verres présentant le défaut pour le traitement T1 dans cet échantillon. On peut justifier qu'il s'agit d'une loi binomiale en donnant les paramètres correspondants. Pour calculer la probabilité d'avoir exactement 10 paires de verres présentant ce défaut dans l'échantillon, on utilise la formule de la loi binomiale avec les paramètres n = 50 et p = 0,1. On trouve une probabilité de 0,015. L'espérance du nombre de défauts dans un échantillon de 50 paires est égale à 5, en utilisant la formule de l'espérance pour une loi binomiale. C'est ainsi que se conclut cet exercice sur les probabilités en utilisant la transcription d'une vidéo.