 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Additif alimentaire pour les agneaux (1)
Dans cette vidéo, Théobald de Cidéaux explique le principe du titrage par suivi conductimétrique. Il aborde l'exemple du titrage des additifs alimentaires dans les agneaux pour éviter certaines maladies. L'éleveur administre une solution de chlorure d'ammonium à un agneau de 24 kg, et le but de l'exercice est de vérifier si sa préparation est conforme aux recommandations du site des partenaires de la production animale en France.
Le titrage conductimétrique consiste à titrer un volume donné de la solution préparée par l'éleveur avec une solution titrante d'hydroxyde de sodium, et à mesurer la conductivité de la solution pendant le processus.
La première question de l'exercice demande de déterminer si la réaction chimique entre le chlorure d'ammonium et l'hydroxyde de sodium est une réaction acido-basique ou une réaction d'oxydo-réduction. En analysant les ions NH4+ et HO-, on constate qu'il y a un transfert de protons (H+), ce qui indique qu'il s'agit d'une réaction acido-basique.
Ensuite, il est demandé de réaliser un schéma légendaire du dispositif de titrage conductimétrique. Le schéma proposé comprend une bécher, une burette graduée, une sonde reliée au conductimètre, et une potence avec un agitateur magnétique.
On nous montre ensuite une courbe obtenue à la fin du titrage, et on nous demande d'exprimer la concentration en quantité de matière de chlorure d'ammonium de la solution préparée par l'éleveur, puis de calculer sa valeur. En analysant l'équation de la réaction de titrage, on détermine que les réactifs ont été introduits en proportion stoichiométrique, ce qui permet d'établir une relation entre les quantités de matière des deux espèces chimiques. En utilisant cette relation, on détermine la concentration de la solution préparée par l'éleveur grâce aux données du titrage.
Ensuite, on nous demande de proposer un encadrement de la concentration de la solution préparée par l'éleveur en prenant en compte les incertitudes. On utilise les incertitudes absolues des différentes verreries utilisées dans le titrage pour déterminer l'incertitude absolue sur la concentration.
Enfin, on nous demande de calculer la masse de chlorure d'ammonium apportée quotidiennement par l'éleveur à l'agneau, et de comparer ce résultat à la valeur préconisée par le site des partenaires de la production animale en France. On utilise la concentration de la solution préparée par l'éleveur et la quantité de solution donnée à l'agneau pour calculer la masse de chlorure d'ammonium. On compare ensuite cette valeur à celle préconisée par le site, en prenant en compte une marge d'erreur de 10%.
L'éleveur a donc bien respecté les recommandations du site, car la masse de chlorure d'ammonium donnée à l'agneau se situe dans l'intervalle préconisé.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Additif alimentaire pour les agneaux (2)
Bonjour à tous! Dans cette vidéo, nous nous intéressons au code Python nécessaire pour simuler un titrage par conductimétrie. Nous avons utilisé l'exemple d'un éleveur donnant des compléments alimentaires à son agneau et nous avons effectué un titrage pour évaluer la concentration de la solution donnée à l'animal. Nous avons donc titré les ions NH4+ grâce aux ions HO-.
Dans la première partie, nous avons complété le code aux lignes 6, 7 et 8. Les variables A, B et C correspondent aux nombres stoichiométriques des espèces chimiques dans l'équation de réaction. Dans notre cas, A=1, B=1 et C=1 car les nombres stoichiométriques de tous les réactifs et produits dans notre équation sont égaux à 1.
Ensuite, nous avons identifié les deux espèces chimiques correspondant aux variables NSA et NSB. NSA représente la quantité de matière en ions Cl- (chlorure) et NSB représente la quantité de matière en ions Na+ (sodium).
Ensuite, nous avons analysé les 5 graphiques obtenus à l'aide du programme Python. Nous avons utilisé un tableau de présence des différentes espèces chimiques en solution pour déterminer quelles espèces étaient représentées sur chaque graphique. Avant l'équivalence, les ions HO- sont ajoutés et réagissent immédiatement avec les ions NH4+, conduisant à une diminution de la quantité de matière en NH4+ et à la formation de NH3. Après l'équivalence, les ions HO- et Na+ sont ajoutés mais les ions NH4+ ne sont plus présents en solution.
Enfin, nous avons complété le code aux lignes 12 (calcul du volume à l'équivalence) et 19 (calcul de Nb). Le volume à l'équivalence correspond à la quantité de matière en ions HO- apportée à l'équivalence, ce qui peut être calculé en utilisant les concentrations et volumes initiaux des réactifs. Nb représente la quantité de matière en ions HO- en solution, qui est nulle avant l'équivalence car les ions HO- sont ajoutés et consommés immédiatement en réagissant avec les ions NH4+.
J'espère que ce résumé en SEO friendly du cours vous a été utile. Si vous avez des questions, n'hésitez pas à les poser en commentaire!
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

test greg
Dans cette vidéo, nous étudions la caractérisation de l'orbite d'un satellite dans le cadre de la mission GRAFO. Deux satellites jumeaux sont envoyés sur la même orbite. L'attraction gravitationnelle de la planète varie légèrement d'un mois à l'autre en raison d'une fraction infime de sa masse qui est en mouvement constant. Cette variation peut rendre l'attraction gravitationnelle tantôt centripète tantôt non centripète.
Dans la première partie, nous nous intéressons à la caractérisation de l'orbite. Les satellites de cette mission ont une orbite quasi-circulaire avec une altitude de 490 km par rapport à la Terre. L'inclinaison du plan de la trajectoire par rapport à l'équateur est de 89 degrés. Les deux satellites sont situés à une distance L l'un de l'autre.
Nous examinons les forces qui s'appliquent sur ces satellites, en nous concentrant sur le mouvement d'un satellite pour le moment. Nous devons d'abord dessiner un schéma représentant la Terre, le rayon RT, le satellite et le vecteur n qui est le vecteur unitaire du satellite vers la Terre.
Ensuite, nous devons donner l'expression vectorielle de la force gravitationnelle F exercée par la Terre sur le satellite. En notant cette force sur le schéma, nous pouvons exprimer cette force gravitationnelle en utilisant la formule G fois la masse de la Terre fois la masse du satellite divisé par la distance Terre-satellite au carré, portée par le vecteur n.
Nous déduisons ensuite l'expression du champ vectoriel terrestre G à partir de l'expression de la force gravitationnelle. Le champ gravitationnel est donc G fois la masse de la Terre fois la masse du satellite divisé par RT plus z au carré, porté par le vecteur n.
En considérant uniquement l'action de la Terre, nous établissons l'expression vectorielle de l'accélération a du satellite en utilisant le principe fondamental de la dynamique. L'accélération est donc gmt sur rt plus z au carré, portée par le vecteur n.
Ensuite, nous démontrons que dans le cadre de l'approximation d'une orbite circulaire, le mouvement du satellite est uniforme. Pour cela, nous supposons que l'orbite est circulaire et montrons que lorsque le mouvement est circulaire, l'accélération tangentielle est nulle, ce qui signifie que la vitesse du satellite est constante et donc que le mouvement est uniforme.
En concluant cette partie de l'exercice, nous expliquons que si vous avez des questions, n'hésitez pas à les poser en commentaire et que nous y répondrons avec plaisir.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

test greg
Dans cette vidéo, Théobald de Studio aborde la caractérisation de l'orbite d'un satellite dans le cadre de la mission GRAFO, qui envoie deux satellites jumeaux sur la même orbite. Il mentionne que l'attraction gravitationnelle de la planète varie faiblement en raison du mouvement continu d'une fraction de la masse terrestre, ce qui peut rendre cette attraction gravitationnelle tantôt centripète et tantôt non.
Dans la première partie de la vidéo, Théobald se concentre sur la caractérisation de l'orbite des satellites. Il explique que l'orbite est quasi-circulaire, avec une altitude z de 490 km, et une inclinaison du plan de trajectoire à l'équateur de 89°. Il nous informe également que les deux satellites sont situés à une distance L l'un de l'autre, et examine les forces appliquées sur ces satellites. Il ne se penche que sur le mouvement d'un satellite pour le moment. Il nous demande de représenter la Terre, son rayon RT, et le satellite avec son centre de masse S, ainsi que le vecteur unitaire n allant du satellite vers la Terre.
Ensuite, il nous demande de donner l'expression vectorielle de la force gravitationnelle F de T sur S exercée par la Terre sur le satellite. Théobald suggère de refaire le schéma et de noter la force F de T sur S, qui est dirigée du satellite vers la Terre. Il explique que cette force gravitationnelle peut être exprimée comme G masse de la Terre fois masse du satellite divisé par la distance Terre-satellite au carré, portée par le vecteur n. Il souligne que cette force est attractive et doit attirer le satellite et la Terre, donc elle est dirigée vers la Terre.
Ensuite, il nous demande de déduire l'expression du champ vectoriel terrestre G. En utilisant la relation entre la force gravitationnelle et le champ gravitationnel, Théobald calcule l'expression du champ gravitationnel, qui est G masse de la Terre fois masse du satellite divisé par RT plus z au carré, porté par le vecteur n.
Il poursuit en établissant l'expression vectorielle de l'accélération a du satellite en considérant uniquement l'action de la Terre. En utilisant le principe fondamental de la dynamique, Théobald montre que la somme des forces extérieures est égale à la masse du satellite multipliée par son accélération. En utilisant l'expression de la force gravitationnelle calculée précédemment, il trouve l'expression de l'accélération, qui est g fois masse du satellite divisé par RT plus z au carré, toujours portée par le vecteur n. Il note que l'accélération est égale au champ gravitationnel g dans ce cas.
Ensuite, il montre que dans le cadre de l'approximation d'une orbite circulaire, le mouvement du satellite est uniforme. Il explique que pour un mouvement circulaire, l'accélération peut être décomposée en une accélération tangentielle et une accélération normale. En utilisant cette décomposition et l'expression de l'accélération, il montre que si le mouvement est circulaire, la vitesse du satellite est constante.
Pour conclure cette première partie de la vidéo, Théobald invite les spectateurs à poser leurs questions dans les commentaires et promet de répondre avec plaisir.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI
Analyse d’un pigment à base d’oxyde de fer (1)
Dans cette vidéo, nous nous intéressons à l'analyse d'un pigment à base d'oxyde de fer. Un pigment est une espèce chimique colorante et insoluble dans le milieu qu'elle colore. Nous allons analyser une poudre colorante contenant un pigment d'oxyde de fer de formule Fe2O3. Le fabricant indique que la teneur en oxyde de fer de cette poudre est de 5%. Nous allons effectuer une analyse quantitative de ce produit en utilisant une méthode de dosage par étalonnage.
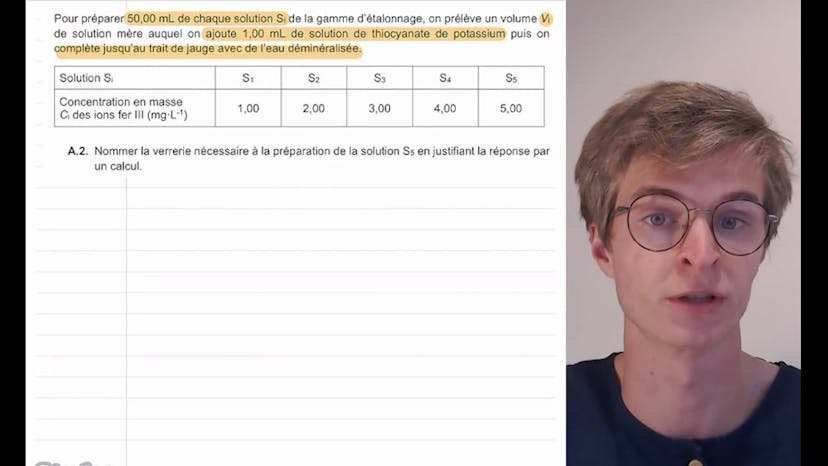
Dans une première étape, nous préparons une gamme d'étalons contenant des ions fer 3. Pour cela, nous préparons une solution mère S0 contenant des ions fer 3 en utilisant du chlorure de fer 3 hexahydraté (FeCl3-6H2O). Nous devons écrire l'équation de dissolution de ce composé et déterminer la masse de solide nécessaire pour obtenir la solution S0.
L'équation de dissolution du chlorure de fer 3 hexahydraté est FeCl3-6H2O -> Fe3+ + 3Cl- + 6H2O. La masse de solide nécessaire pour obtenir la solution S0 est calculée en utilisant la quantité de matière en ion fer 3, qui est égale à la quantité de matière en chlorure de fer 3 hexahydraté. Nous obtenons une masse de 3,0 x 10-2 g.
Ensuite, nous préparons différentes solutions de la gamme d'étalonnage en diluant la solution mère S0. Nous devons estimer le volume à prélever de la solution mère pour préparer la solution S5. Nous utilisons la conservation de la quantité de matière et de la masse pour trouver que le volume à prélever est de 10,0 mL. Nous utiliserons une pipette jaugée de 10,0 mL pour cette étape.
Ensuite, nous réalisons un spectre d'absorption d'une solution du ion fer 3 en présence du ion thiocyanate, dans les mêmes conditions que les solutions de la gamme étalon. Nous devons déterminer la couleur de la solution en utilisant la méthode du maximum d'absorption. Nous trouvons que la solution est de couleur rouge.
Enfin, nous devons indiquer la longueur d'onde la plus adaptée pour effectuer les mesures d'absorbance. La longueur d'onde la plus adaptée correspond au maximum d'absorption, qui est d'environ 490 nm dans ce cas.
N'hésitez pas à poser vos questions en commentaire et nous nous retrouverons pour la suite de l'exercice.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI
Analyse d’un pigment à base d’oxyde de fer (2)
Dans cette vidéo, Théobald de Cidéo aborde le sujet de l'analyse d'un pigment à base d'oxyde de fer. Le pigment est insoluble dans le milieu qu'il colore et le fabricant prétend que la teneur en oxyde de fer de la poudre est de 5%. Pour vérifier cela, un dosage par étalonnage est effectué.
La première partie de l'exercice consiste à préparer une gamme étalon contenant des ions de fer. Ensuite, une courbe d'étalonnage est réalisée en mesurant l'absorbance des solutions S1 à S5 avec un spectrophotomètre réglé à la longueur d'onde lambda0. La représentation graphique de cette courbe est compatible avec la loi de Berlembert, qui établit une relation entre l'absorbance et la concentration. La droite obtenue passe par l'origine, ce qui montre que l'absorbance est proportionnelle à la concentration molaire.
Pour établir la relation exprimant l'absorbance en fonction de la concentration en masse d'ion fer 3, on trace une droite qui passe au-dessus et en dessous des points de mesure. En choisissant deux points arbitraires sur cette droite, on peut calculer la constante K qui est égale à la différence d'ordonnées divisée par la différence d'abscisses.
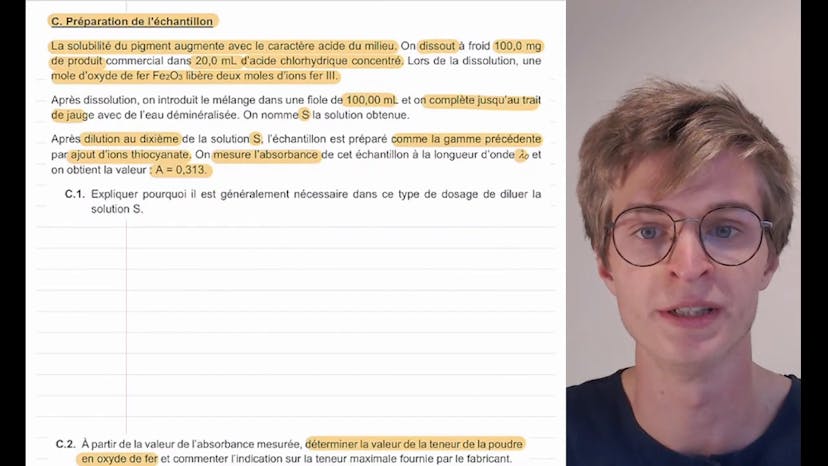
La troisième partie de l'exercice concerne la préparation de l'échantillon. Pour augmenter la solubilité du pigment, 100mg de produit sont dissous dans 20mg d'acide chlorhydrique concentré. Ensuite, le mélange est introduit dans une fiole de 100mg et complété avec de l'eau déminéralisée. Par dilution au dixième, la solution S est préparée et ensuite l'absorbance de l'échantillon est mesurée à la longueur d'onde lambda0.
Il est généralement nécessaire de diluer la solution S dans ce type de dosage car la loi de Berlembert s'applique pour des solutions diluées. En utilisant la valeur de l'absorbance mesurée, on peut déterminer la teneur de la poudre en oxyde de fer. Cette teneur est donnée par la masse d'oxyde de fer dans la poudre divisée par la masse de la poudre. En effectuant les calculs nécessaires, on obtient une teneur de 5,1%, ce qui est conforme à l'indication du fabricant.
Il s'agit d'un exercice complexe mais formateur pour comprendre les dosages par étalonnage. Théobald encourage les spectateurs à travailler dessus et à poser des questions dans les commentaires si besoin.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Le vin et ses composants (1)
Le cours porte sur la mesure de la concentration d'ions fer dans un vin blanc afin de déterminer le risque de précipité blanc dans celui-ci. Pour cela, un titrage spectrophotométrique est réalisé en plusieurs étapes. Tout d'abord, les ions fer 2+ présents dans le vin sont oxydés en ions fer 3+. Ensuite, les ions fer 3+ réagissent avec des ions thiocyanate pour former un composé coloré, le FeSCN2+. La couleur de ce composé est rouge, ce qui permet de faire un étalonnage et de déterminer la concentration en Fe-SCN2+ grâce à sa couleur. A partir de là, on peut déterminer la teneur en fer dans le vin blanc étudié. La relation entre l'absorbance et la concentration en fer est proportionnelle, conformément à la loi de Beer-Lambert. En mesurant l'absorbance de la solution de vin, on peut déterminer la concentration massique de fer dans celui-ci. Dans le cas étudié, la concentration en fer est inférieure à 10 mg par litre, ce qui signifie qu'il n'y a pas de risque de précipité blanc dans le vin.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Le vin et ses composants (2)
Dans cette vidéo, Théobald de Cidéo aborde l'exercice de chimie sur l'estérification dans le vin, qui a été donné au bac en Asie l'année dernière. Il se concentre sur la durée de la synthèse d'un ester du vin en laboratoire et comment la relier aux conditions expérimentales.
Le protocole expérimental consiste à mélanger 115 ml d'acide éthanoïque pur avec 17 ml d'éthanol pur dans un bain de glace. Ensuite, 2 ml du mélange réactionnel sont prélevés dans 7 tubes différents. Une solution d'hydroxyde de sodium est préparée dans une burette pour le titrage des tubes.
La première question abordée est pourquoi le mélange réactionnel est placé dans un bain de glace avant le temps T0 et avant le titrage. Il explique que la température est un facteur cinétique, et en abaissant la température, on ralentit la réaction. Ainsi, le bain de glace empêche la réaction de se produire avant le titrage.
Ensuite, il est demandé de montrer que le mélange réactionnel est équimolaire. Théobald calcule la quantité de matière d'acide éthanoïque et d'éthanol en utilisant leurs masses volumiques et molaires fournies dans l'énoncé, et il obtient des quantités de matière égales.
Il est ensuite demandé de vérifier que la quantité d'acide contenue dans chaque tube à la date T0 est de 17,3 millimoles. En utilisant les concentrations initiales du mélange réactionnel, il montre que la concentration en acide dans les tubes est la même que celle de la solution initiale, et fait une application numérique pour obtenir la valeur demandée.
Ensuite, il explique le rôle du bleu de thymol, qui est un indicateur coloré utilisé pour repérer l'équivalence lors du titrage. Il change de couleur dans une plage de pH spécifique, ce qui permet de repérer facilement l'équivalence. Il montre également comment la quantité d'acide restant dans chaque tube à la date Ti peut être calculée à l'aide de la formule CbxVbi.
Il établit ensuite un tableau d'avancement de la transformation chimique, démontrant comment la quantité d'éthanoate d'éthyle produite dans chaque tube peut être liée à la quantité d'acide restant.
Enfin, il donne les résultats expérimentaux dans un tableau et demande la valeur de la quantité de matière N2 manquante. En utilisant la formule précédente, il calcule cette quantité et obtient une valeur de 6,0 x 10-3 mol.
En conclusion, Théobald résume l'exercice et annonce qu'il continuera à traiter les questions restantes dans la prochaine vidéo.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Le vin et ses composants (3)
Dans ce cours, le sujet principal est la vitesse d'apparition des estères lors du processus d'estérification du vin. Pour déterminer cette vitesse, l'orateur utilise un graphe représentant la quantité d'estère formée en fonction du temps.
La vitesse volumique d'apparition des estères est définie comme étant 1 sur le volume de la solution, multiplié par la dérivée du nombre de moles d'estères par rapport au temps. En examinant les tangentes tracées sur le graphe, on constate que le coefficient directeur de la tangente diminue au cours du temps, ce qui signifie que la vitesse volumique d'apparition diminue également.
Pour déterminer la valeur de la vitesse volumique d'apparition de l'ester à un moment donné (t = 20 minutes), la formule utilisée est la suivante : v = 1/v * dn/dt. En effectuant les calculs nécessaires avec les coordonnées de la tangente à t = 20 minutes, la valeur obtenue pour la vitesse volumique d'apparition est de 6,0 x 10^-2 moles par litre par minute.
Ensuite, l'orateur aborde la notion de temps de demi-réaction. Celui-ci correspond au temps au bout duquel la quantité de matière initiale en réactif limitant est divisée par deux. Dans ce cas précis, puisque l'estérification se produit dans des proportions équimolaires, le temps de demi-réaction correspond également au moment où la moitié de l'ester est apparue. En traçant la courbe et en utilisant la quantité de matière finale divisée par deux, on peut déterminer le temps de demi-réaction, qui est de 6,5 minutes.
En comparant ce temps de demi-réaction à celui évoqué en introduction (qui peut être de plusieurs jours voire de plusieurs mois), on constate un écart important. L'explication avancée est que les réactifs utilisés dans l'expérience étaient purs et donc très concentrés, ce qui a accéléré la vitesse de réaction. L'hypothèse est que la concentration des réactifs joue un rôle significatif dans la valeur de t1 demi.
Finalement, ce cours met en avant l'importance de la pureté et de la concentration des réactifs dans la vitesse de réaction. Les réactifs purs et concentrés permettent une réaction plus rapide, contrairement à des réactifs moins purs ou dilués.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Formule 1 et freinage
Dans cet exercice, nous étudions la prise de risque des pilotes de Formule 1 lorsqu'ils décélèrent avant les virages. Les circuits de Formule 1 pourraient être redessinés pour minimiser ces risques. Lors d'un freinage avant un virage, les pilotes subissent des décélérations de plus de 6G, ce qui est supérieur à ce que les astronautes subissent au décollage. L'objectif de l'exercice est d'étudier la prise de risque d'un pilote pendant un freinage.
Nous étudions le mouvement du système voiture plus pilote, en se concentrant sur le mouvement de son centre de masse dans un référentiel terrestre galiléen. Le système se déplace horizontalement en ligne droite et freine entre les points A et B. Différentes forces agissent sur le système : le poids, la réaction normale du support et une force de freinage opposée au mouvement.
En appliquant la deuxième loi de Newton, nous démontrons que les coordonnées du vecteur d'accélération sont ax2t = -f/m et ay2t = 0. Après avoir réalisé un schéma de la situation et fait un bilan des forces, nous appliquons le principe fondamental de la dynamique. En projetant cette équation selon les axes x et y, nous obtenons les équations pour ax2t et ay2t.
Ensuite, nous justifions que la variation de vitesse (delta v) entre les points A et B est égale à ax * delta t, en utilisant le fait que l'accélération est la dérivée de la vitesse par rapport au temps. Puisque les points A et B sont proches, delta t peut être approximé par dt et delta v2x peut être assimilé à dv2x, ce qui permet d'établir la formule.
Nous calculons ensuite la valeur de l'accélération en m/s2 à partir des données de va, vb et delta t. L'accélération est de -44 m/s2. Pour comparer cette accélération à la valeur de 6G mentionnée dans le texte, nous divisons a par 1G (9,81 m/s2), ce qui donne un résultat de 4,5G. Cela indique que le pilote subit une décélération moins importante que celle mentionnée dans le texte.
Nous utilisons ensuite un graphique qui représente la limite de tolérance d'un individu à l'accélération pour déterminer si le pilote prend un risque pour sa santé lors du freinage. Nous constatons que le pilote reste dans une zone de faible risque, ce qui signifie qu'il ne prend pas de risque pour sa santé lors du freinage.
Dans la deuxième partie de l'exercice, nous comparons l'évolution de la vitesse en fonction du temps prédite par le modèle avec les mesures réelles obtenues grâce à un capteur embarqué. En exprimant vx en fonction de t, nous obtenons une fonction affine de la vitesse. Cependant, la courbe expérimentale ne correspond pas totalement à celle prédite par le modèle, ce qui remet en question l'hypothèse de la constance de la force de frottement pendant tout le freinage.
En conclusion, cet exercice étudie la prise de risque des pilotes de Formule 1 lors du freinage avant les virages. Il propose une modélisation du mouvement et compare les résultats avec des mesures expérimentales pour évaluer la validité du modèle.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Observation de la division de Cassini (1)
Dans cette transcription de la vidéo, l'auteur explique comment observer la division de Cassini à travers une lunette astrologique. Il commence par expliquer pourquoi la division de Cassini ne peut pas être distinguée à l'œil nu, en utilisant des concepts tels que le diamètre apparent et le pouvoir de résolution de l'œil. Ensuite, il montre que le grossissement minimal nécessaire pour observer la division de Cassini est d'environ 89. Il poursuit en expliquant comment modéliser la lunette astronomique à l'aide de deux lentilles convergentes, identifiant l'objectif comme la première lentille la plus proche de l'objet et l'oculaire comme la lentille derrière l'objectif. Ensuite, il construit l'image de AB par la première lentille et représente le faisceau émergent délimité par les rayons issus de B traversant la lunette. Enfin, il annonce que dans la vidéo suivante, il va aborder le choix de l'oculaire pour observer correctement la division de Cassini.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI
Observation de la division de Cassini (2)
Dans cette vidéo, Théobald de Studio nous explique comment observer la division de Cassini grâce à une lunette astronomique. L'objectif est de déterminer quel oculaire choisir pour observer correctement la division.
Dans la première partie de l'exercice, on modélise la lunette par un objectif suivi d'un oculaire, avec un plan focal image dans le plan focal objet de l'oculaire. On trace les rayons qui traversent les deux lentilles et on cherche à déterminer la position de l'image finale B' du point B à travers la lunette. On constate que l'image finale est à l'infini, ce qui confirme que la lunette est afocale, c'est-à-dire qu'elle donne une image à l'infini lorsqu'on observe un objet à l'infini. Cela permet de regarder à travers la lunette sans avoir besoin d'accommoder.
Ensuite, on nous demande d'indiquer sur le schéma le diamètre apparent de l'angle θ' de l'image θ' à travers la lunette. Le diamètre apparent correspond à l'angle sous lequel on observe B' à travers la lunette, et on le voit sur le schéma à cet endroit.
On nous demande ensuite de calculer la relation entre le grossissement et les distances focales f' et f''. Le grossissement est donné dans l'énoncé comme étant θ' sur θ. Pour calculer θ, on peut se référer au schéma et on obtient tanθ = a1, b1 / f1'. De la même manière, tanθ' = a1, b1 / f2'. En simplifiant, on peut établir que θ ≈ tanθ et θ' ≈ tanθ'. En utilisant ces approximations, on trouve que le grossissement g = f1' / f2'.
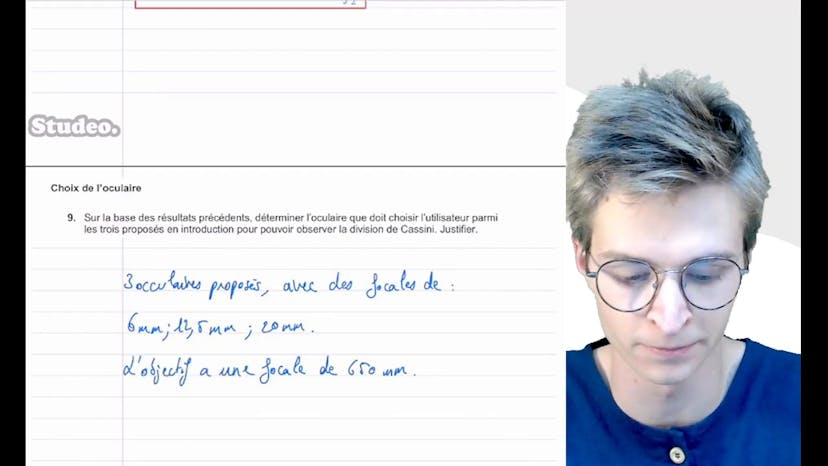
Enfin, on nous propose trois oculaires avec des focales différentes de 6mm, 12.5mm et 20mm, ainsi qu'un objectif de 650mm. On utilise la formule du grossissement pour déterminer quelle oculaire choisir. On trouve que l'oculaire avec une focale de 6mm donne un grossissement de 108, ce qui est supérieur à 89 (le minimum requis pour observer Cassini). L'oculaire avec une focale de 12.5mm donne un grossissement de 52, inférieur à 89, donc il ne convient pas. Le troisième oculaire avec une focale de 20mm donne aussi un grossissement inférieur à 89. Finalement, on choisit l'oculaire avec la plus petite focale, c'est-à-dire l'oculaire 1 avec une focale de 6mm, qui permettra d'observer correctement la division de Cassini.
En conclusion, ce cours explique comment observer la division de Cassini avec une lunette astronomique et comment choisir l'oculaire approprié pour cette observation.


