Cours d'apprentissage en ligne

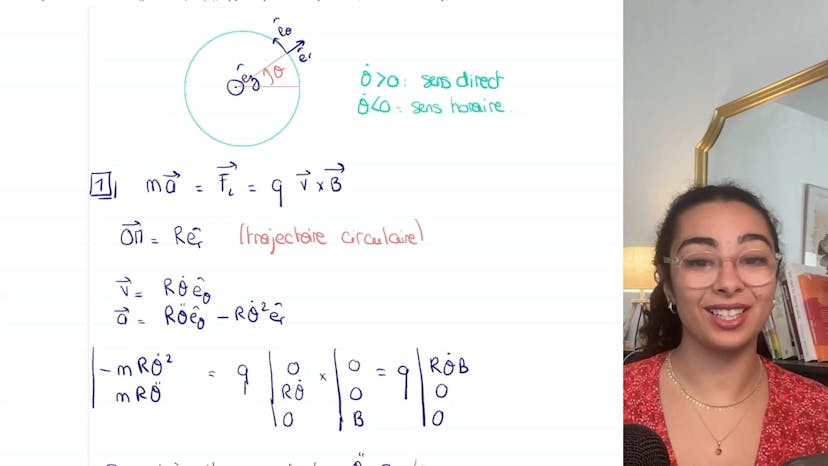
Pulsation de cyclotron

La leçon porte sur la pulsation cyclotron d'une particule en mouvement dans un champ magnétique constant. La trajectoire est circulaire et le sens de parcours est déterminé par la vitesse angulaire θ'. L'équation de la particule est donnée par MA = QV×B, où M est la masse, A est l'accélération, Q est la charge, V est la vitesse et B est l'intensité du champ magnétique. En analysant les composantes cinématiques, on trouve que la vitesse V est Rθ'Eθ et l'accélération A est Rθ''Eθ - Rθ'^2ER. En appliquant le principe fondamental de la dynamique, on obtient MRθ'² = QRθ'B. Ainsi, θ' = -QB/M, où θ' est la pulsation cyclotron. Si Q est positif, θ' est négatif, ce qui correspond à un sens de parcours dans le sens horaire. Si Q est négatif, θ' est positif, ce qui correspond à un sens de parcours dans le sens antihoraire. La pulsation cyclotron est donnée par θ' = QB/M. Il est important de retenir cette formule, ainsi que la relation entre la vitesse angulaire θ' et le sens de parcours de la trajectoire.

Sélecteur de vitesse

Dans cette vidéo, nous avons étudié un exercice sur un sélecteur de vitesse qui implique une particule chargée se déplaçant dans un champ électrique et magnétique. Pour que la vitesse de la particule reste inchangée, il faut que la somme des forces exercées sur la particule soit nulle. Cela signifie que la force de Lorentz, qui est la seule force agissant sur la particule dans ce cas, doit être égale à zéro. En résolvant cette expression, nous trouvons que le produit de la charge, du champ électrique et de la vitesse initiale doit être égal à zéro. Dans la deuxième partie de la vidéo, nous explorons comment ce dispositif peut être adapté en tant que sélecteur de vitesse. L'idée est de récupérer uniquement les particules ayant une certaine vitesse. Pour ce faire, nous observons que la force de Lorentz est composée de deux parties, l'une tendant à accélérer les particules (force électrique) et l'autre tendant à les faire tourner (force magnétique). Si la vitesse de la particule change, cela signifie que la force de Lorentz n'est pas nulle. Cependant, en choisissant une valeur précise de la vitesse initiale, nous pouvons obtenir une particule se déplaçant en ligne droite. Ainsi, en plaçant un dispositif de collecte, tel qu'une fente, à la fin de la trajectoire rectiligne de la particule, nous pouvons sélectionner uniquement les particules ayant cette vitesse spécifique. Il est important de noter que pour être précis dans cette sélection, nous devons attendre suffisamment longtemps pour que toutes les trajectoires déviées aient disparu, afin d'éviter de collecter des particules indésirables. La précision de cette sélection dépendra de la vitesse et de la distance parcourue par les particules. Elle permettra de déterminer l'ordre de grandeur de la précision sur la vitesse sélectionnée. En résumé, si la force de Lorentz (q * e * v - q * B * v0) est différente de zéro, la particule sera déviée par le champ magnétique et ne pourra pas être collectée dans le dispositif de sélection.

Champ électrique inconnu

Dans ce cours, nous nous intéressons à un champ électrique inconnu et à la déviation d'une particule à travers ce champ. L'exercice consiste à déterminer la norme du champ électrique et l'angle de déviation de la trajectoire. Pour commencer, nous devons déterminer la direction du champ électrique statique U0. On sait que le champ électrique tend à accélérer les électrons en changeant leur trajectoire. Donc, l'électron est dévié vers le haut, ce qui signifie que la force électrique le pousse vers le haut (UY). Étant donné que l'électron a une charge négative, la force électrique est opposée au champ électrique, ce qui implique que E est opposé à UY. Ensuite, nous devons déterminer le signe de la variation de l'énergie cinétique (ΔEC), c'est-à-dire si elle augmente ou diminue. Comme la vitesse de la particule est toujours positive le long de la trajectoire, la puissance apportée par la force électrique est positive, ce qui signifie que la différence d'énergie cinétique est également positive. Maintenant, nous devons trouver la norme de E0. Pour cela, nous utilisons le travail de la force électrique entre l'entrée et la sortie du champ, qui est égal à moins E fois E0 fois la distance ES (delta Y). En utilisant la ligne droite entre E et S pour simplifier notre calcul, nous obtenons E times E0 times delta Y. En appliquant le principe fondamental de la dynamique, on trouve les équations horaires du mouvement de la particule. En éliminant le temps, on peut écrire l'équation de la trajectoire en fonction de la position horizontale X. En utilisant la distance L pour X, on obtient une équation reliant E0, L, M et V0. Enfin, nous pouvons déterminer l'angle de déviation de la trajectoire en utilisant la vitesse en Y et la vitesse en X à la sortie du champ. En remplaçant les valeurs avec celles obtenues précédemment, nous trouvons que l'angle de déviation tan alpha est égal à E0L/MV0^2. En utilisant la valeur de l'énergie cinétique obtenue précédemment, nous pouvons calculer cet angle. En résumé, l'exercice consiste à déterminer la norme du champ électrique E0 qui dévie une particule à travers une certaine distance L dans un champ électrique constant. Nous avons également calculé la direction du champ électrique, le signe de la variation de l'énergie cinétique et l'angle de déviation de la trajectoire en fonction des grandeurs données.

Particule alpha dans un champ

Aujourd'hui, nous nous intéressons à une particule alpha dans un champ électrique. Une particule alpha est un ion He²+ qui est composé d'un noyau d'hélium. Dans cet exercice, nous avons un faisceau de particules alpha avec une grande vitesse de 2000 m/s qui entre dans une zone avec un champ électrique uniforme de 1000 volts par mètre. Le champ électrique et la vitesse initiale sont de sens opposés. Tout d'abord, on montre que le poids de la particule peut être négligé par rapport à la force électrique. Ensuite, nous décrivons le mouvement de la particule, qui est un mouvement rectiligne uniformément accéléré. On nous demande ensuite si la particule revient au point d'entrée et la durée passée dans la zone du champ électrostatique. Nous utilisons les équations du mouvement pour montrer que la particule revient à sa position initiale après un certain temps. Enfin, nous expliquons que la vitesse de la particule lorsqu'elle revient est opposée à la vitesse initiale. Cela peut être compris par la conservation de l'énergie cinétique.

Mouvement cyclotron

Aujourd'hui, nous allons étudier le mouvement cyclotron, une démonstration classique sur les particules chargées. Nous considérons une particule de charge Q et de masse M qui évolue dans un champ magnétique B selon l'axe OZ. La particule a une vitesse initiale selon l'axe EY. L'objectif est de déterminer le mouvement de la particule dans cette configuration. Nous négligeons le poids de la particule et ne considérons que la force magnétique. Nous commençons par rappeler les expressions des vecteurs vitesse (V) et accélération (A) en coordonnées cartésiennes et les appliquer au Principe Fondamental de la Dynamique (PFD). Pour calculer la force de Lorentz, nous utilisons la formule QV ⊗ B. En projetant cette force sur les deux directions qui nous intéressent, nous obtenons les équations X = QBY/M et Y = QBX/M, que nous appelons équations couplées. Nous voulons résoudre ces équations couplées. Une méthode consiste à dériver l'équation pour obtenir une équation de la forme d'un oscillateur harmonique. Une autre méthode consiste à utiliser une grandeur intermédiaire complexe U = X' + Y'. En dérivant U par rapport au temps, nous obtenons une équation de la forme U' = - Y ωc U, où ωc est la pulsation cyclotronique (QBM). Nous résolvons cette équation en fonction des conditions initiales pour obtenir U(t) = IV0e^(-iωct). Cependant, U n'a pas de sens physique, donc nous séparons sa partie réelle (qui correspond à VX) de sa partie imaginaire (qui correspond à VY). Finalement, nous obtenons X(t) = V0 sin(ωct) et Y(t) = V0 cos(ωct), ce qui représente le mouvement de la particule dans le plan XY. Nous intégrons encore une fois ces équations pour obtenir les expressions de X(t) et Y(t) en fonction du temps. Ainsi, nous trouvons X(t) = V0/(ωc) (1 - cos(ωct)) et Y(t) = V0/(ωc) sin(ωct). La trajectoire de la particule correspond à ces équations et elle forme un cercle. Nous le démontrons en utilisant le théorème de Pythagore pour éliminer les cos² et sin². La vitesse de la particule sur le cercle est constante et égale à V0, tandis que sa vitesse angulaire est égale à ωc. Cela signifie que la particule parcourt le cercle à une vitesse constante et avec une vitesse angulaire déterminée par les propriétés du champ magnétique. Dans le cas d'une particule de charge négative, les équations restent les mêmes, à l'exception du signe de ωc, qui devient négatif. Cela entraîne des changements dans les coordonnées du centre du cercle, mais la trajectoire reste un cercle. En conclusion, l'exercice du mou

Spectromètre de masse

Dans cette vidéo, Leïla explique le fonctionnement d'un spectromètre de masse. Un spectromètre de masse permet de déterminer la composition d'un système du point de vue de la chimie, en identifiant les différents ions présents. Le dispositif vise à séparer les ions en fonction de leur masse et éventuellement de leur charge. Les ions sont accélérés par une tension appliquée entre la chambre d'ionisation et la chambre d'accélération. Le champ électrique accélère les ions dans la même direction et les fait tourner autour de l'axe de déplacement grâce à la force magnétique de Lorentz. Dans cet exercice, on nous demande de déterminer la vitesse à laquelle les ions passent par le trou O en fonction de U, Q et M. Le théorème de l'énergie cinétique permet de trouver la vitesse initiale des ions à la sortie de la chambre d'ionisation. Ensuite, on nous demande de déterminer la trajectoire des ions une fois qu'ils pénètrent dans une zone où règne un champ magnétique perpendiculaire à leur vitesse. La trajectoire des ions est circulaire et leur rayon dépend de leur masse, charge, vitesse initiale et champ magnétique. Enfin, on nous demande de calculer la distance entre les points d'impact de deux isotopes sur une plaque de détection. Les isotopes sont des ions Mg2+ avec des masses différentes (24 et 26). La différence entre les isotopes réside dans le nombre de neutrons dans leur noyau, ce qui affecte leur masse. La distance entre les points d'impact dépend du rayon de la trajectoire des ions, qui dépend à son tour de la masse, de la charge, de la vitesse initiale et du champ magnétique. Le résultat obtenu pour la distance entre les points d'impact est de 3,7 mm, ce qui paraît cohérent pour la construction d'un spectromètre de masse.

Circuits couplés

Aucun résumé n'est disponible pour cette vidéo

Bobine longue

Dans cette vidéo, Matisse de Studio explique le concept d'autoinductance et d'inductance propre d'une bobine longue. Il commence par modéliser la bobine par un solénoïde, dans lequel les effets de bord sont négligés. Le champ magnétique à l'intérieur de la bobine est défini comme étant égal à μ0N/LI, où μ0 est la permittivité du vide, N est le nombre de spires et L est la longueur du solénoïde. Ensuite, il détermine le flux propre de la bobine en utilisant l'intégrale du champ magnétique sur toute la surface de la bobine, ce qui donne μ0N²S/LI. À partir de là, il définit l'auto-inductance L comme étant le flux propre divisé par le courant, soit μ0N²S/L. En appliquant la loi de Faraday, il obtient l'équation différentielle du courant de la bobine en fonction de la force électromotrice E0, soit dI/dt + (R/L)I = E0/L. Il explique ensuite l'effet de l'auto-inductance sur la variation du courant et conclut en analysant le bilan de puissance du circuit, où la puissance délivrée par le générateur peut être dissipée par effet Joule ou stockée sous forme d'énergie magnétique dans la bobine.

Solénoïdes emboîtés

Dans cette vidéo, nous étudions des solénoïdes emboîtés, S1 et S2, d'axes OZ, de longueur L, de nombre de spires N, et de rayons R1 et R2. Nous supposons que la longueur L est bien plus grande que les rayons, ce qui fait que nous parlons de bobine longue. La bobine 2 est en court circuit, tandis que la bobine 1 est parcourue par un courant d'intensité I1(t) = I * cos(ωt), avec I = 1A. Dans la première partie du cours, nous devons déterminer les coefficients d'induction propre L1 et L2. Pour cela, nous devons calculer le flux propre généré par chaque bobine. Ensuite, nous utilisons ces flux pour trouver les valeurs de L1 et L2. Nous trouvons que L1 = μ0 * N² * S1 / L et L2 = μ0 * N² * S2 / L. Ensuite, nous devons déterminer le coefficient d'induction mutuelle M. Pour ce faire, nous pouvons calculer le flux généré par le champ magnétique du circuit 1 vers le circuit 2 ou vice versa. Nous trouvons que M = μ0 * N² * S2 / L. 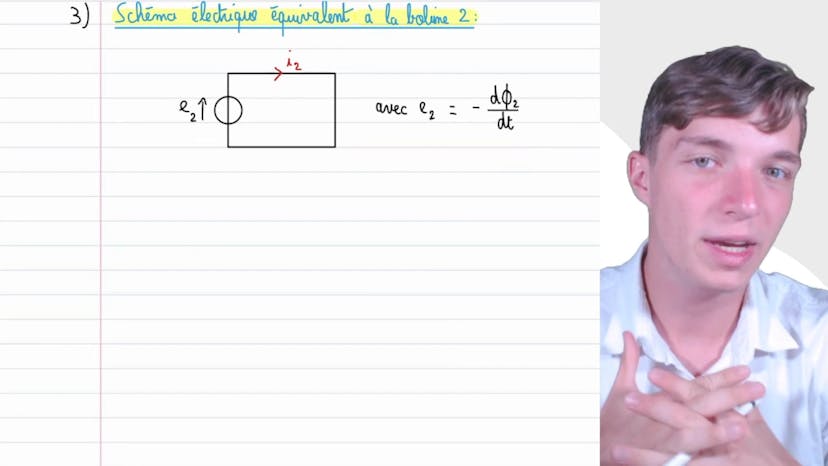Finalement, nous devons exprimer le courant I2 circulant dans la bobine 2. En utilisant les schémas équivalents et les lois de comportement, nous trouvons que I2 = (M / L2) * I1. En conclusion, nous avons calculé les coefficients d'induction propre et mutuelle ainsi que le courant circulant dans la bobine 2 pour des solénoïdes emboîtés. Ce cours nécessite une certaine attention aux calculs des flux et aux coefficients d'inductance, mais il sert de base pour des exercices plus complexes.

Mesure de M

Dans cette vidéo, Matisse de Studio explique un montage permettant de mesurer le coefficient d'inductance mutuelle entre deux bobines. Le premier circuit est classique avec une force électromotrice, une résistance et une bobine L1, tandis que le deuxième circuit est simplement une bobine L2. L'objectif est de déterminer l'intensité parcourant la bobine 2 et la tension U2 en fonction de la tension U1 et du coefficient d'inductance mutuelle M. D'abord, il est souligné que la bobine 2 est en court-circuit, donc aucune force électromotrice ou condensateur ne peut délivrer un courant dans ce circuit, ce qui signifie que l'intensité I2 est égale à 0. Ensuite, il est expliqué que la tension U2 dans le cadre de la loi classique de comportement de la bobine est égale à 0, car la tension aux bornes de la bobine 2 serait toujours nulle. Cependant, étant donné que le circuit 2 est plongé dans le champ magnétique créé par le circuit 1, les bobines sont affectées, ce qui perturbe les courants et les tensions résultants. Il est donc nécessaire de prendre en compte le circuit 1 dans l'expression de la tension U2 en utilisant le concept d'inductance mutuelle. La troisième question aborde donc l'expression de U2 en fonction de M et U1. L'inductance mutuelle est définie comme le flux du champ magnétique créé par le circuit 1 sur le circuit 2. On introduit également la notion d'auto-inductance, qui est le flux généré par le circuit 1 sur lui-même. Finalement, on obtient l'expression de U2 en fonction de I1, nécessitant de déterminer la relation entre I1 et U1 en utilisant la loi d'Ohm. Il est alors expliqué que lorsqu'il y a une dérivée dans la relation entre U1 et U2, comme c'est le cas ici, il est utile de passer par les nombres complexes pour simplifier les calculs. En utilisant les grandeurs complexes correspondant au régime sinusoidal forcé, on trouve que le coefficient d'inductance mutuelle M est égal à rU2/(2πfU1). En appliquant les valeurs numériques données dans l'exercice, U1 = 3V et U2 = 0.5V, on peut calculer M, qui est égal à 1.3 milli Henry. Ensuite, l'exercice demande de déterminer sans calcul la modification de M lorsque la bobine est tournée à 180 degrés et à 90 degrés. Lorsque la bobine est tournée à 180 degrés, seule l'inversion des branchements de l'oscilloscope se produit, donc M reste sensiblement le même. En revanche, lorsque la bobine est tournée à 90 degrés, très peu de lignes de champ magnétique du circuit 1 traversent la bobine 2, ce qui donne un coefficient d'inductance mutuelle d'environ 0. En conclusion, cet exercice détaillé permet de comprendre comment mesurer le coefficient d'inductance mutuelle entre deux circuits grâce à un montage particulier.

Négliger l'auto-induction ?

Dans cette vidéo, on se demande si on peut négliger le phénomène d'autoinduction dans un circuit, en particulier dans les circuits sans bobine. On étudie un circuit avec une bobine d'autoinductance L, une résistance R, et un champ magnétique extérieur B. On utilise des notations complexes pour résoudre les équations différentielles, et on exprime le module de H, qui représente le rapport des tensions complexes d'autoinductance par rapport au champ extérieur. On obtient une condition sur la pulsation pour négliger la force électromotrice auto-induite. En utilisant des valeurs typiques pour R et L, on calcule numériquement la pulsation, qui doit être très inférieure à 1x10^4 rad/s. On conclut en remarquant que pour un circuit avec une seule spire, on peut négliger l'autoinduction, car on se trouve à une fréquence très inférieure à 3x10^8 Hz.