 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Nombres et calculs
Seconde

Factoriser avec a²-b²
Dans cet exercice, on apprend à factoriser à l'aide des trois identités remarquables : a plus b au carré, a moins b au carré, et a moins b facteur de a plus b. Pour factoriser une expression, on doit identifier les termes et choisir l'identité remarquable correspondante. Ensuite, on peut utiliser les formules pour trouver la valeur de a et la valeur de b, puis écrire l'expression sous forme de a-b fois a plus b. Dans l'exemple donné, on factorise l'expression 4x²-16 en utilisant l'identité remarquable numéro 3. On obtient finalement 2x-4 fois 2x plus 4.
Maths
Géométrie
Seconde

Qu'est-ce qu'une distance ?
Dans cet exo, on apprend comment trouver la distance entre un point et une droite en utilisant la définition de la distance qui est la distance entre le point et son projeteur orthogonal sur la droite en question. En utilisant un triangle rectangle ABC, on veut trouver la distance entre le point C et la droite AB. En trouvant le projeteur orthogonal de C sur la droite AB, on remarque que le point A est en fait le projeteur orthogonal de C sur la droite AB et donc la distance entre C et la droite AB est égale à la distance entre A et B qui est la longueur de l'hypoténuse du triangle ABC.
Maths
Stats et Probas
Seconde

Augmentation en % d'une série statistique
Dans cet exercice, on apprend comment calculer une augmentation générale d'une série statistique en utilisant les moyennes avant et après. L'augmentation de tous les termes d'une série de x% équivaut à une augmentation de sa moyenne de x%. Pour comprendre pourquoi c'est vrai, on peut utiliser la formule de la moyenne et le fait que pour déterminer l'augmentation de x%, on multiplie par 1 plus x sur 100. En appliquant cela à un exemple où la moyenne est passée de 11,2 à 12,768, on peut résoudre l'équation pour trouver que l'augmentation est de 14%.
Maths
Fonctions
Seconde

Inéquation avec x²
Ce cours explique comment résoudre l'inéquation x² < 7 en utilisant la méthode générale pour résoudre une inéquation x² ≤ k ou x² ≥ k. Si k est négatif, il n'y a pas de solution pour x² < k car x² est toujours positif ou nul. Si k est positif, x² ≤ k a pour solution l'intervalle [−√k, √k) et x² > k a pour solution (−∞, −√k) ∪ (√k, ∞). Comme k = 7 est positif, l'inéquation x² < 7 a pour solution l'intervalle (−√7, √7).
Maths
Nombres et calculs
Seconde

Factorisation multiple
Dans cet exercice de mathématiques, on cherche à factoriser une expression compliquée en utilisant des identités remarquables. Après avoir examiné les termes et les signes, on identifie que l'expression x² + 6x + 9 peut être factorisée en (x + 3)². Ensuite, on utilise cette identité remarquable pour factoriser l'expression de départ en (x + 3) (x + 3 - 2x + 3). En regroupant les termes, on obtient finalement l'expression factorisée en x + 3 ( -x + 6).
Maths
Nombres et calculs
Seconde

Produit en croix
Dans cet exercice, on apprend à résoudre une équation avec une égalité de fractions en la transformant en produit. Après avoir développé l'équation, le second degré s'en va, permettant de résoudre l'équation classiquement. Avec X différent de -1,5 et 1, la solution est trouvée grâce à une opération de division. L'équation de départ avec les fractions a pour solution X égal à 3 sur 5.
Maths
Géométrie
Seconde

Des points alignés
Dans cet exercice, on apprend à démontrer que le point C appartient à la droite AB en montrant que les points A, B et C sont alignés. Pour cela, il faut calculer les distances entre les points et vérifier si l'égalité BA + AC = BC est vraie. En utilisant la formule des longueurs et en vérifiant les abscisses des points, on détermine que A est entre B et C. Finalement, en simplifiant les calculs de distance, on montre que l'égalité est vraie, prouvant ainsi que le point C appartient à la droite AB.
Maths
Fonctions
Seconde

Comparaison de racines
Dans ce cours, on apprend comment comparer deux nombres donnés sous forme de fractions avec des racines carrées. On utilise des inégalités successives en commençant par le plus petit noyau, puis en appliquant des fonctions croissantes ou décroissantes comme la racine carrée ou la fonction inverse. On rappelle que la racine carrée est croissante sur les nombres positifs et que la fonction inverse est décroissante sur les nombres positifs. Finalement, on peut obtenir une inégalité entre les deux nombres à comparer en appliquant ces méthodes avec des exemples concrets. On obtient donc que 2 sur 3 plus racine de 5 est strictement plus grand que 2 sur 3 plus racine de 7.
Maths
Fonctions
Seconde

Déterminer la parité
Dans cet exercice, nous apprenons comment déterminer si une fonction est paire ou impaire. Une fonction est paire si son ensemble de définition est centré en 0 et si f (-x) est égal à f(x) pour tout x dans son ensemble de définition. Si f(-x) est égal à (-f)x, la fonction est impaire. Pour vérifier si une fonction est paire ou impaire, nous devons calculer f(-x) et voir si nous obtenons f(x) ou -f(x). De plus, l'ensemble de définition doit être centré en 0, ce qui signifie que si un nombre est dans l'ensemble de définition, son opposé doit également être dans l'ensemble de définition. Dans l'exemple donné, la parité d'une fonction est déterminée en vérifiant si f(-x) est égal à f(x) en utilisant l'ensemble de définition donné. La fonction était f(x) = 3x² -1, et il est montré qu'elle est paire.
Maths
Nombres et calculs
Seconde
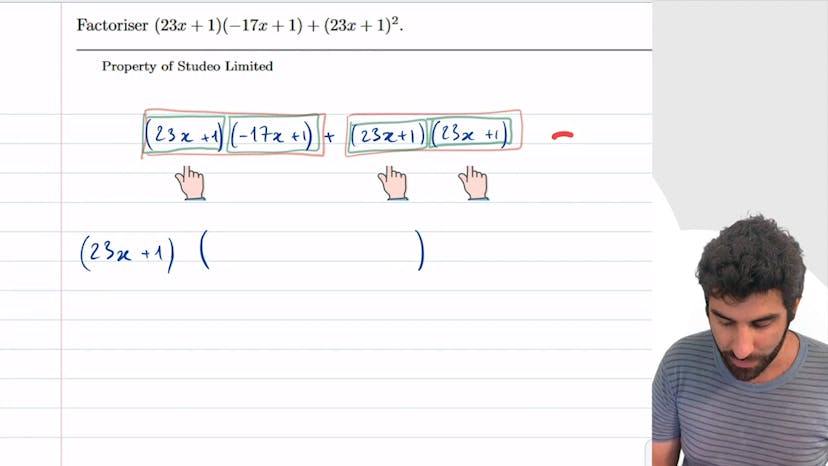
Reconnaître un facteur commun
Dans cet exercice de maths, la méthode pour factoriser une expression utilisée consiste à réécrire l'expression pour trouver tous les facteurs qu'elle contient. Ensuite, on repère les termes en commun dans les deux côtés de l'expression. On met ces termes communs en parenthèses et on distribue le reste des termes en soustrayant les facteurs communs. Enfin, on simplifie et on regroupe pour obtenir la forme factorisée. En appliquant cette méthode, l'expression 23x² + 46x + 21 peut être factorisée en (23x + 1)(6x + 2).
Maths
Nombres et calculs
Seconde
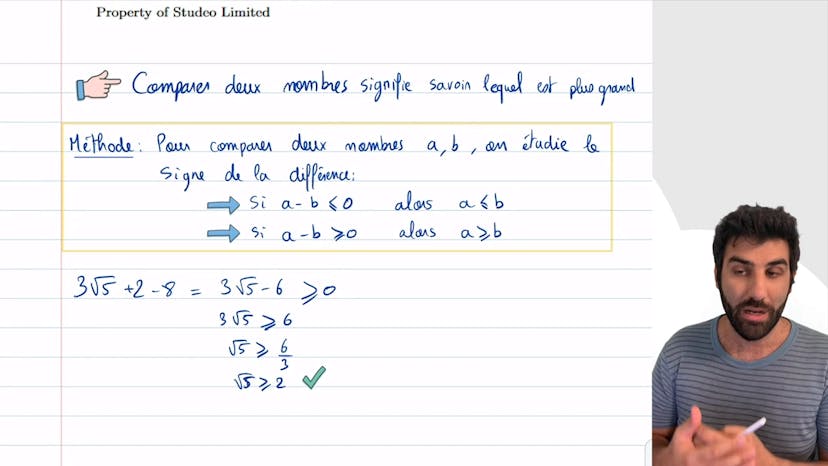
Comparer des racines
Dans cet exo, nous allons comparer trois nombres sans utiliser une calculatrice. La méthode pour cette comparaison est de soustraire le plus petit nombre du plus grand et vérifier si le résultat est positif ou négatif. Nous allons tester la méthode avec les nombres 3 racines de 5, 2 et 8. En simplifiant 3 racines de 5 moins 6, nous obtenons 3 racines de 5 supérieur égal à 6 sur 3, qui est égal à racine de 5 supérieur égal à 2. Nous pouvons donc conclure que 3 racines de 5 plus 2 est plus grand que 8. Si le résultat avait été différent, nous aurions recommencé en utilisant des inégalités opposées.
Maths Spé
Probabilités
Terminale

Avec et sans ordre de tirage
Le cours explique comment déterminer le nombre de mains possibles de 5 cartes dans un jeu de 32 cartes avec certaines configurations spécifiques. Pour commencer, il est expliqué qu'un carré d'As fixe déjà 4 cartes sur les 5. Ensuite, il est précisé qu'il y a 28 mains possibles avec le carré d'As, ce qui est considéré comme rare. Ensuite, il est abordé le cas des 5 cartes de la même couleur, en précisant qu'il y a 4 couleurs dans le jeu de 32 cartes et qu'il faut sélectionner 5 cartes parmi 8 de la même couleur. En multipliant cela par 4, on obtient le nombre total de mains possibles avec les cartes de la même couleur. Ensuite, il est expliqué comment déterminer le nombre de mains avec exactement une paire. Il faut choisir les 2 cartes de la paire parmi 30 cartes restantes, puis choisir les 3 cartes restantes parmi les autres cartes du jeu sans choisir les mêmes cartes que celles de la paire. Ce raisonnement est fait pour chaque hauteur possible (3, 4, 5, 6, 7, 8, 9, 10, Valet, Dame, Roi, As), ce qui donne le nombre total de mains possibles avec exactement une paire. Le raisonnement consiste à diviser en deux à chaque étape, en fixant une variable et en calculant le nombre de possibilités pour chaque variable.


