Tous les sujets
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Généralités et Fonctions de Référence
- Variations et Extremums
- Signe et Inéquations
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI
Physique-Chimie
Corrigés de BAC- Prépa Examens
- Révisions Maths lycée
- Tous les sujets
- Maths
- Nombres et calculs
- Géométrie
- Fonctions
- Généralités et Fonctions de Référence
- Variations et Extremums
- Signe et Inéquations
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI - Physique-Chimie
- Corrigés de BAC
- Prépa Examens
- Révisions Maths lycée
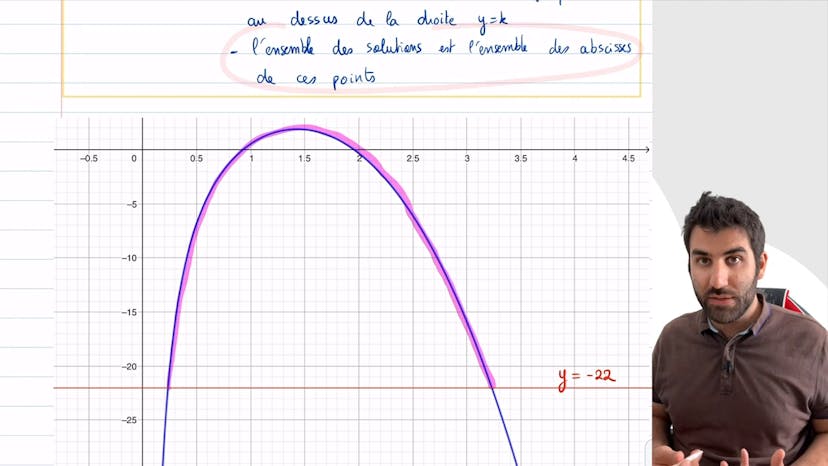
Inéquation avec x²
Ce cours explique comment résoudre l'inéquation x² < 7 en utilisant la méthode générale pour résoudre une inéquation x² ≤ k ou x² ≥ k. Si k est négatif, il n'y a pas de solution pour x² < k car x² est toujours positif ou nul. Si k est positif, x² ≤ k a pour solution l'intervalle [−√k, √k) et x² > k a pour solution (−∞, −√k) ∪ (√k, ∞). Comme k = 7 est positif, l'inéquation x² < 7 a pour solution l'intervalle (−√7, √7).
