Tous les sujets
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Généralités et Fonctions de Référence
- Variations et Extremums
- Signe et Inéquations
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI
Physique-Chimie
Corrigés de BAC- Prépa Examens
- Révisions Maths lycée
- Tous les sujets
- Maths
- Nombres et calculs
- Géométrie
- Fonctions
- Généralités et Fonctions de Référence
- Variations et Extremums
- Signe et Inéquations
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI - Physique-Chimie
- Corrigés de BAC
- Prépa Examens
- Révisions Maths lycée
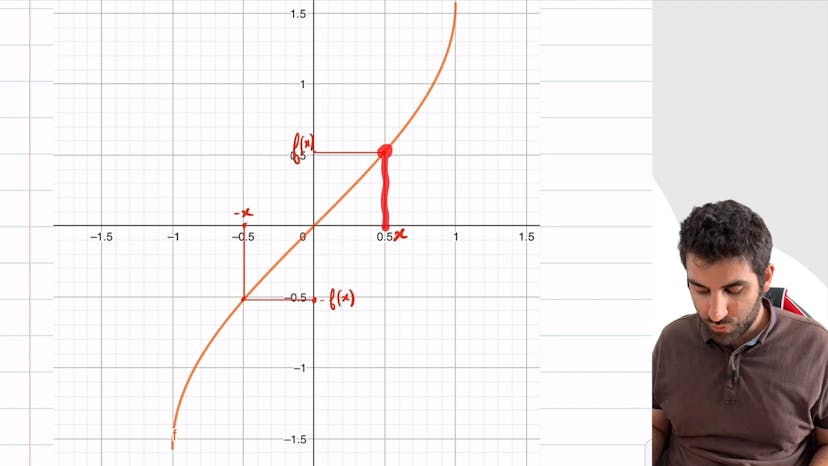
Résolution graphique : inéquation
Dans cet article, nous allons voir comment résoudre une inéquation graphiquement en trois étapes. Premièrement, nous devons tracer la courbe de la fonction f(x) supérieure à k. Deuxièmement, nous traçons la droite d'équation y=k. Enfin, nous repérons l'ensemble des points de la courbe au-dessus de la droite pour trouver l'ensemble des abscisses qui nous intéressent. Dans notre exemple, nous trace la courbe de f(x), traçons la droite y=-22, repérons l'ensemble des points au-dessus de la droite, puis nous trouvons que l'intervalle de solution graphique est entre 0,22 et 3,23.
