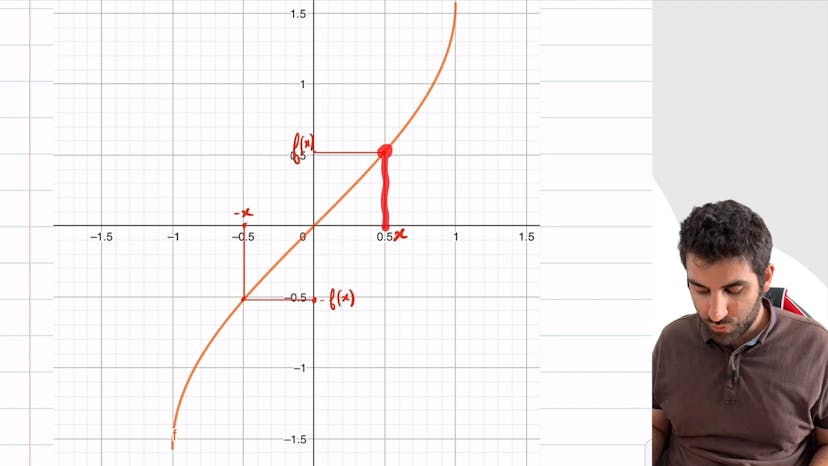
Tracer une fonction symétrique

Dans cet exercice, nous apprenons à tracer la courbe symétrique par rapport à la première bissectrice d'une autre courbe. La première bissectrice est une droite qui passe par des points ayant la même abscisse que l'ordonnée. Pour tracer une courbe, nous devons faire un tableau de valeurs qui nous donne les coordonnées des points, que nous placon sur un graphique et nous les relions pour former la courbe. Pour trouver la courbe symétrique, nous devons inverser les coordonnées de la courbe initiale par rapport à l'axe Y = X. Nous faisons ensuite un tableau de valeurs de ces points qui nous donneront les nouvelles coordonnées. Nous plaçons ces points sur un graphique, en renversant l'axe des ordonnées et des abscisses et les reliant pour former notre courbe symétrique. Dans cet exercice, notre courbe symétrique est celle de la fonction racine carré.