Déterminer la parité

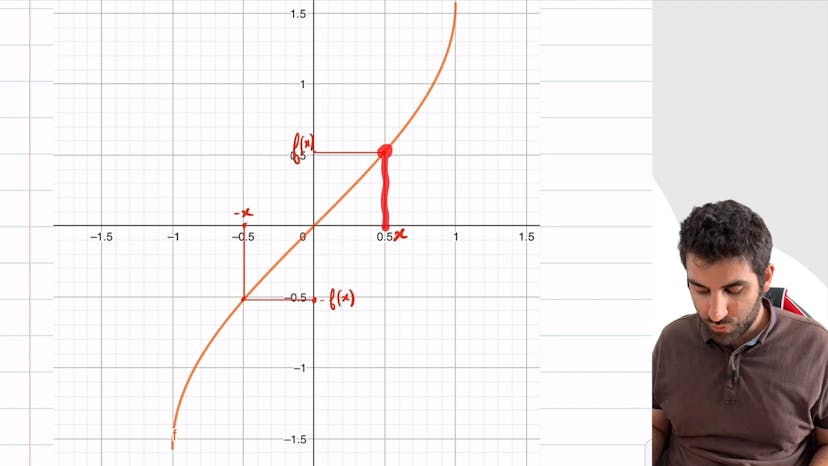
Dans cet exercice, nous apprenons comment déterminer si une fonction est paire ou impaire. Une fonction est paire si son ensemble de définition est centré en 0 et si f (-x) est égal à f(x) pour tout x dans son ensemble de définition. Si f(-x) est égal à (-f)x, la fonction est impaire. Pour vérifier si une fonction est paire ou impaire, nous devons calculer f(-x) et voir si nous obtenons f(x) ou -f(x). De plus, l'ensemble de définition doit être centré en 0, ce qui signifie que si un nombre est dans l'ensemble de définition, son opposé doit également être dans l'ensemble de définition. Dans l'exemple donné, la parité d'une fonction est déterminée en vérifiant si f(-x) est égal à f(x) en utilisant l'ensemble de définition donné. La fonction était f(x) = 3x² -1, et il est montré qu'elle est paire.