Cours d'apprentissage en ligne

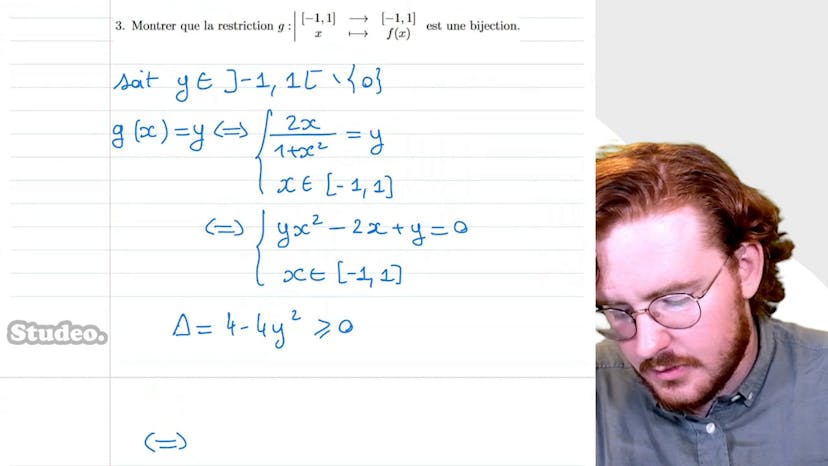
Injection, surjection : exemple

Dans cette vidéo sur les fonctions à variable réelle, Paul explore l'injectivité, la surjectivité et la bijectivité. Il prend une fonction f définie par 2r dans R, avec f(x) = 2x/(1+x^2). Paul utilise le graphique de f pour montrer que f n'est pas injective car f(1.5) = 4.5 et f(2) = 4.5. Il calcule ensuite le delta de l'équation f(x) = 2 degré, ce qui montre que f n'est pas surjective non plus.Paul prouve ensuite que l'image de f est le segment [-1,1], ce qui montre que f est surjective lorsqu'elle est restreinte à cet intervalle. Enfin, il montre que la restriction de f à l'intervalle [-1,1] est bijective en trouvant des expressions pour la solution unique à l'équation g(x) = y.

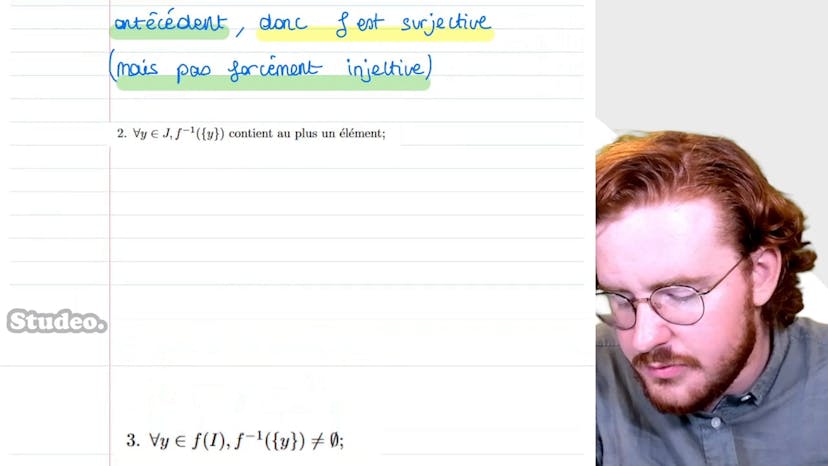
Injection, surjection : propriétés

Le cours traite des notions d'injectivité, de surjectivité et de bijection dans les applications mathématiques. Il énonce quatre propriétés permettant de déterminer si une fonction est injective, surjective ou bijective, ou si aucun de ces termes ne s'applique. Pour résumer, l'injectivité signifie qu'un élément de l'ensemble d'arrivée admet au plus un antécédent, la surjectivité signifie que tout élément de l'ensemble d'arrivée a au moins un antécédent et la bijection combine ces deux propriétés en affirmant que chaque élément de l'ensemble d'arrivée a un unique antécédent. Les propriétés énoncées permettent également de déduire qu'une fonction peut être surjective mais pas injective, injective mais pas surjective, bijective ou ne répondre à aucune de ces catégories.

Ensembles images

Dans cette vidéo, Paul parle de la manipulation d'images entre deux ensembles, E et F, et explique comment démontrer que A est inclus dans B en implique F de A inclus dans F de B. Il montre également que l'inclusion réciproque n'est pas toujours vraie. Ensuite, il démontre que F de A inter B est inclus dans F de A intersection F de B, mais que l'inclusion réciproque n'est pas toujours vraie. Enfin, il explique que l'image de l'union d'un ensemble est égale à l'union des images de cet ensemble, mais que cela n'est vrai que dans un sens pour l'intersection.

Relation d'équivalence

Dans cette vidéo, on explore la relation d'équivalence R définie pour les ensembles des réels où X est en relation avec Y si X exponentielle de Y est égale à Y exponentielle de X. Pour montrer qu'une relation est une relation d'équivalence, il faut démontrer que la relation est réflexive, symétrique et transitive, tout comme l'égalité. La relation R est donc une relation d'équivalence.Ensuite, la question 2 demande de préciser, pour chaque réel X, le nombre d'éléments dans la classe d'équivalence de X (c'est-à-dire, combien de réels sont en relation avec X selon R). On introduit la fonction T(t) = t exponentielle de -t et on note C2x la classe d'équivalence pour X. En réarrangeant l'énoncé de la relation R, on trouve que C2x est l'ensemble Y tel que F2x égale F2y où F(t) = t exponentielle de -t.Pour trouver les antécédents de F2x (c'est-à-dire, les réels en R qui sont en relation avec X selon R), on étudie le graphe de F, qui est dérivable, et on remarque qu'il y a deux parties, X supérieur à 0 et X inférieur ou égal à 0. Pour X supérieur à 0, la classe d'équivalence a deux éléments, et pour X inférieur ou égal à 0, la classe d'équivalence a un élément. Ainsi, le nombre d'éléments dans la classe d'équivalence de X dépend du signe de X.

On redéfinit l'injectivité

Dans cette vidéo, on parle de la preuve de l'équivalence entre deux propositions P1 et P2, où P2 est l'injectivité de la fonction f. La question est de trouver la négation des deux propositions avec des quantificateurs, pour prouver que non P1 est équivalent à non P2. Pour cela, il est conseillé de traduire les propositions en français avant de les traduire en quantificateurs et de prendre la négation. Ensuite, la video nous guide à travers les étapes pour prouver les deux sens de cette équivalence, en utilisant la négation des propositions. Finalement, la preuve montre que P1 et P2 sont équivalentes.

Bijection dans N

Dans cette vidéo, Paul aborde l'exercice sur la bijectivité et montre comment démontrer qu'une fonction est bijective. Il explique que pour prouver l'injectivité, il faut trouver des relations entre les nombres entiers, les diviseurs, et les nombres pairs et impairs. Pour prouver la surjectivité, il faut décomposer un nombre en facteurs premiers et trouver l'existence de son antécédent. À partir de là, il montre comment composer f avec une bijection de n étoiles dans n pour obtenir une bijection de n² dans n, en utilisant une application simple qui associe n à n-1. En résumé, l'exercice consiste à prouver la bijectivité d'une fonction et à trouver une bijection de n² dans n.

Somme et produits

En calcul algébrique, on doit évaluer des expressions sous forme de somme et de produit. Pour une somme, on utilise le symbole SOM (sigma majuscule) qui peut être lu comme la somme pour k allant de 0 à n de x. Il faut ensuite remplacer k par une valeur de 0 à n à chaque terme et les ajouter. On peut également utiliser des propriétés comme la somme des 1 qui vaut (n+1) et sortir un facteur prénuméraire. Pour un produit, on utilise le symbole PI (pi majuscule) qui fonctionne de la même manière que la somme. Il est donc possible de sortir un facteur prénuméraire. En résumé, il ne faut pas se formaliser avec les symboles, mais plutôt se concentrer sur ce qu'ils représentent. Les réponses pour les QCM de l'exercice sont : B pour la somme, 1 pour la somme de moins 1 puissance p et B pour le produit.

Reconnaissance de formes

Dans cette vidéo, Matisse de Studio nous montre comment déterminer des primitives de fonctions sur un intervalle donné. Pour cela, il nous explique deux méthodes. La première, un peu bruteforce, consiste à tout développer, ce qui prend beaucoup de temps. La deuxième méthode consiste à repérer une forme particulière de fonction à une puissance donnée et à faire apparaître sa dérivée dans l'expression grâce à des calculs. Ensuite, on peut appliquer des formules de référence pour déterminer la primitive. Matisse applique cette méthode à plusieurs exemples de fonctions pour illustrer cette démarche. Il rappelle également l'importance de connaître les formules de référence pour les fonctions usuelles telles que les puissances, les racines et les logarithmes.

Intégration par parties 1

Dans cette vidéo, Matisse de Studio explique comment résoudre deux intégrales en utilisant la méthode d'intégration par parties. Pour la première intégrale, il calcule l'intégrale de 0 à 1 de x exponentielle x dx en choisissant x comme sa fonction u et exponentielle de x comme sa fonction v'. Ensuite, il calcule les fonctions correspondantes et vérifie les hypothèses nécessaires avant d'appliquer le théorème d'intégration par parties pour trouver la réponse de l'intégrale, qui est égale à 1. Pour la deuxième intégrale, Matisse utilise la même méthode en choisissant ln de x comme sa fonction u et x carré comme sa fonction v'. Il calcule les fonctions correspondantes, vérifie les hypothèses et applique le théorème d'intégration par parties pour trouver la réponse de cette intégrale, qui est égale à 2 neuvième de e3 plus 1 neuvième. Il souligne également l'importance de bien retenir la syntaxe d'intégration par parties et de vérifier les hypothèses pour éviter les erreurs.

Intégration par parties 2

Dans cette vidéo, nous abordons le sujet des primitives pas très usuelles en mathématiques. Nous commençons par le cas de la fonction Arc Tangente. Pour déterminer une primitive de cette fonction, nous utilisons le théorème fondamental de l'analyse, qui permet de trouver automatiquement une primitive. Plus précisément, une primitive de Arc Tangente est donnée par l'intégrale de 0 à x de Arc Tangente de t dt. Pour calculer cette intégrale, nous utilisons la technique de l'intégration par parties. En posant u = Arc Tangente de t et v' = 1, nous obtenons une expression simplifiée de l'intégrale. En effectuant les calculs nécessaires, nous obtenons finalement une primitive de Arc Tangente, qui est donnée par la fonction x Arc Tangente de x - 1/2 ln(1 + x²). Nous passons ensuite à la détermination d'une primitive de ln(x²). Encore une fois, nous utilisons le théorème fondamental de l'analyse pour poser l'intégrale à calculer. En utilisant l'intégration par parties avec u = ln(t) et v' = ln(t), nous obtenons une expression simplifiée de l'intégrale. En effectuant les calculs, nous trouvons une primitive de ln(x²), qui est donnée par la fonction x ln(x)² - 2x ln(x) + 2x. Enfin, nous abordons le cas de la fonction sinus(ln(x)). En utilisant à la fois l'intégration par parties et le théorème fondamental de l'analyse, nous obtenons une expression intégrée de cette fonction. En effectuant les calculs, nous trouvons une primitive de sinus(ln(x)), qui est donnée par la fonction 1/2 x sinus(ln(x)) - x cosinus(ln(x)). En conclusion, lorsque nous sommes confrontés à des fonctions dont les primitives ne sont pas usuelles, nous pouvons utiliser le théorème fondamental de l'analyse pour poser l'intégrale à calculer. Ensuite, nous pouvons appliquer des techniques comme l'intégration par parties ou le changement de variable pour simplifier cette intégrale et déterminer la primitive de la fonction donnée.

Changement de variables 1

Dans cette vidéo, Matisse de Studio montre comment effectuer des changements de variables pour calculer des intégrales. La première intégrale est l'intégrale de 1 à 4 de 1-√t sur √dt, qu'il nomme i. Il utilise la formule de changement de variable pour résoudre l'intégrale, en posant x égal à φt qui est égale à √t. En effectuant les étapes nécessaires, il obtient la valeur de i, qui est moins 1. La deuxième intégrale est l'intégrale de 0 à π de sin2t sur 1 plus cos²t dt, qu'il résout en posant x égal à cos2t. En vérifiant les hypothèses requises, il utilise le théorème de changement de variable pour obtenir la valeur de l'intégrale, qui est π sur 2. Enfin, la troisième intégrale est l'intégrale de 1 à e de 1 sur 2t ln de t plus t dt, qu'il résout en posant x égal à ln de t. Après avoir effectué les calculs nécessaires, il obtient que la valeur de l'intégrale est ln de 3 sur 2. Matisse souligne l'importance de bien maîtriser les changements de variables en adaptant la syntaxe et en les réutilisant de façon appropriée.