Cours d'apprentissage en ligne

Moyennes

Dans cette vidéo, Matisse de Studio explique différentes manières de calculer une moyenne, à savoir la moyenne arithmétique, la moyenne géométrique et la moyenne harmonique. Il montre ensuite différentes inégalités entre ces moyennes, en utilisant des manipulations simples, telles que l'inversion ou la sommation. Il recommande également d'utiliser des équivalences au brouillon pour vérifier la validité des propositions. Enfin, il conclut en soulignant l'importance de se servir de ce qui a été fait avant pour démontrer des inégalités ou des relations entre les différentes moyennes.

Partie entière

Bonjour à tous, dans cette vidéo, nous allons aborder les parties entières et démontrer différentes propriétés les concernant. Tout d'abord, pour représenter la partie entière d'un nombre réel X, nous utilisons la notation [X]. Notre objectif est de montrer que pour tout réel X, [X+1] = [X]+1. Pour cela, nous utilisons la définition de la partie entière, qui dit que pour un entier relatif K, [K] est inférieur strictement à X et inférieur ou égal à X+1. En utilisant cette définition et la propriété selon laquelle il n'y a qu'un seul entier relatif strictement compris entre X et X+1, nous montrons que [X+1] = [X]+1. Cette propriété est valable pour l'addition de tous les entiers. Ensuite, nous abordons la démonstration de la propriété selon laquelle la partie entière de la somme de deux nombres réels est inférieure ou égale à la somme des parties entières de ces deux nombres. En utilisant les mêmes relations que précédemment, nous montrons que [X+Y] ≤ [X]+[Y]. Pour cela, nous utilisons la croissance de la partie entière, qui nous permet d'utiliser la relation [X+Y] ≤ [X]+Y. Ensuite, en observant que [Y] est un entier relatif, nous pouvons le sortir de la partie entière pour obtenir [X]+[Y] ≤ [X+Y], ce qui prouve la propriété souhaitée. Enfin, nous examinons une troisième propriété plus technique selon laquelle la partie entière de la somme de trois nombres entiers est inférieure ou égale à la somme des parties entières de ces trois nombres. Nous utilisons une approche par cas en fonction de la position de X et de Y par rapport à leurs parties entières respectives. En évaluant les différentes parties entières, nous montrons que la propriété est vérifiée dans tous les cas. En conclusion, nous pouvons dire que pour tout couple de réels X et Y, la partie entière de X plus la partie entière de Y plus la partie entière de X+Y est inférieure ou égale à 2[X]+2[Y]. Il est important de retenir les différentes relations des parties entières, notamment la définition classique et la méthode de disjonction de cas basée sur la position des nombres par rapport à leur partie entière. Merci d'avoir suivi cette vidéo et à bientôt !

Somme de parties entières

Dans cette vidéo, Baptiste de Studio montre comment démontrer que la somme pour k allant de 0 à n-1 de la partie entière de x plus kn, est égale à la partie entière de nx. Il s'agit d'un exercice compliqué qui nécessite de travailler avec des sommations de parties entières. Baptiste commence par noter que la somme va ajouter des petits décalages à x, ce qui permettra de retrouver la partie entière de nx à la fin. Il pose ensuite une inégalité pour situer x par rapport à sa partie entière et utilise cette inégalité pour évaluer les deux grandeurs recherchées. Enfin, il montre comment identifier la partie entière de x plus k/n et utiliser cette information pour évaluer la somme. Au final, Baptiste démontre que la partie entière de nx est bien égale à la somme des parties entières de x plus k/n.

Partie entière

Dans cette vidéo, Mathis de Studio démontre que pour toute valeur de n, un entier naturel différent de zéro, pour tout réel x, la partie entière de la partie entière de nx divisé par n est égale à la partie entière de x. Pour aborder cet exercice, il conseille de poser des valeurs de n et x quelconques, puis on utilise la relation d'inégalité entre les deux parties entières pour construire la grandeur recherchée. En passant à la partie entière, on démontre la propriété voulue en peu de temps. Mathis conseille de ne pas se formaliser, mais plutôt de montrer qu'on a compris le cours et de manipuler les bonnes relations.

Inéquations trigonométriques

Dans cette vidéo, Mathilde Studio explique comment résoudre des inéquations trigonométriques compliquées. Pour résoudre la première inéquation, elle recommande de représenter le cercle trigonométrique et de limiter les valeurs de cos(x) à une plage spécifique. Pour la seconde inéquation, elle utilise une formule de cosinus pour se ramener à une équation plus gérable. Pour la troisième inéquation, elle ajoute des racines pour utiliser une formule trigonométrique et la résoudre. Enfin, pour la quatrième inéquation, elle utilise une transformation pour isoler cos(x/3) et l'expresser en fonction de cos(pi/4) et sin(x/3) en utilisant une formule trigonométrique. Elle explique comment extraire les solutions sur l'intervalle 0 à 2pi pour obtenir les solutions finales. Elle fournit également des astuces pratiques pour résoudre les inéquations trigonométriques en général.

Formule de duplication

Dans cette vidéo, Mathis de studio explique comment calculer les cosinus et sinus de π sur 8 de manière exacte sans utiliser de calculatrice. Il démontre que π sur 8 peut être ramené à des angles plus connus comme π sur 3, π sur 6 et π sur 4. A partir de là, il utilise la formule classique de cosinus 2x pour trouver la valeur exacte de cosinus 2π sur 8, qui est approximativement égal à 0.92. Il utilise la même logique pour trouver la valeur exacte de sinus 2π sur 8, qui est approximativement égal à 0.38. La démarche est intéressante car elle montre comment trouver des valeurs exactes en utilisant des formules connues.

Formule d'addition

Cette vidéo de Matisse de Studio explique comment calculer les sinus et les cosinus de pi sur 12 de manière exacte. Il explique que même si ce ne sont pas des angles courants, on peut les ramener à des angles de référence tels que pi sur 6, pi sur 3 et pi sur 4. Il donne deux méthodes pour calculer ces angles : diviser pi sur 12 par 2 ou le représenter comme pi sur 3 moins pi sur 4. En utilisant les formules trigonométriques de base, il calcule ensuite le cosinus de pi sur 12 (1 + racine de 3 sur 2 racine de 2) et le sinus de pi sur 12 (racine de 3 moins 1 sur 2 racine de 2). Il conclut en encourageant les gens à utiliser ces méthodes pour ramener les angles rares à des angles connus et à manipuler les formules de la trigonométrie de base.

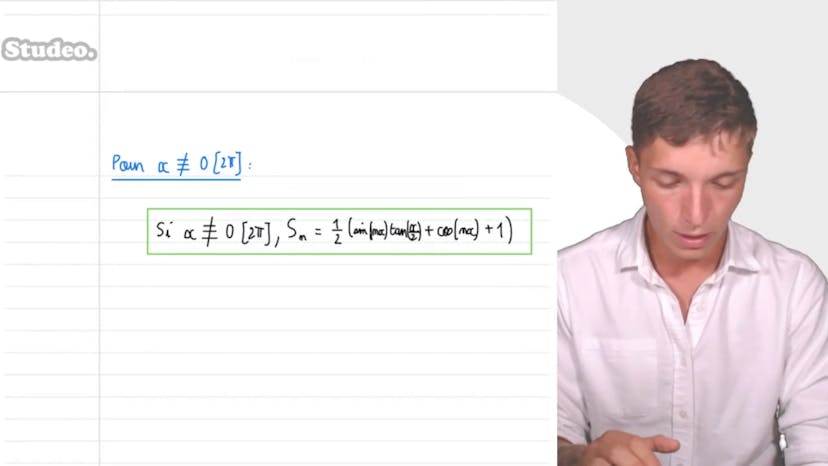
Sommes trigonométriques

Dans cette vidéo, Mathis de Studio explique comment calculer des sommes de cosinus et sinusoïdes. Il commence par expliquer comment calculer la somme pour k allant de 0 à n de cosinus kx, où n est un nombre entier négatif et x est un réel. Il utilise la formule de trigonométrie 2 sin a cos b pour simplifier l'expression. Il en vient alors à la somme télescopique, qui est une somme où la fonction évaluée en n+1 moins la fonction évaluée en 0 donne la somme recherchée. Il applique cette technique pour trouver la somme pour k allant de 0 à n de sinus kx. Ensuite, il utilise cette technique pour trouver la somme pour k allant de 0 à n de cosinus carré kx et la somme pour k allant de 0 à n de sinus carré kx. Enfin, il résume les résultats obtenus pour ces différentes sommes et explique l'importance de la digestion de cas lorsqu'on divise des fonctions trigonométriques.

Autour de la tangente

Dans cette vidéo, Mathijs de studio compare deux approches mathématiques : algébrique et trigonométrique pour résoudre une équation complexe. En utilisant des formules, il calcule la tangente de 3θ en fonction de la tangente de θ. Ensuite, il résout l'équation en utilisant une méthode algébrique qui factorise le polynôme et une méthode trigonométrique qui identifie les racines en utilisant la tangente. Il explique également que la tangente est une fonction bijective de -π/2 à π/2 et que chaque élément a un antécédent sur cette plage. Enfin, il conclut que les deux approches donnent le même ensemble de solutions, mais la méthode trigonométrique est plus élégante.

Parties réelle et imaginaire

Ce cours porte sur les complexes et vise à vérifier les affirmations suivantes. Premièrement, en utilisant la forme algébrique, la somme de la partie réelle des nombres complexes est égale à la partie réelle de la somme. Deuxièmement, la partie réelle de iz est égale à moins la partie imaginaire de z. Troisièmement, pour tout lambda appartenant à R, la partie imaginaire de lambda z est égale à lambda fois la partie imaginaire de z. Quatrièmement, la partie imaginaire du produit de nombres complexes ai n'est pas égale au produit des parties imaginaires. Enfin, si z est différent de 0, 1 sur z est égal au conjugué de z divisé par le module au carré de z, et la partie imaginaire de z divisé par w n'est pas égale à la partie imaginaire de z divisé par la partie imaginaire de w.

Forme algébrique

Cet exercice consiste à transformer des complexes sous forme algébrique en utilisant la technique de multiplication par le conjugué du dénominateur lorsque des i apparaissent à ce niveau. Ensuite, le module carré du complexe est obtenu en faisant la somme des carrés des parties imaginaires et réelles, ce qui permet de simplifier les fractions et de rassembler les résultats pour obtenir la forme algébrique finale. La vidéo montre également une méthode alternative, consistant à poser des variables et à utiliser des symétries pour résoudre le calcul.