Cours d'apprentissage en ligne

Continuité avec paramètres

Dans cette vidéo, on explore la continuité de fonctions et on étudie pour quelle valeur de a la fonction f est continue, ainsi que pour quelle valeur alpha, beta et gamma les fonctions g sont continues. On vérifie également que les morceaux de fonctions sont bien raccordés entre eux, et pour quelles valeurs de constantes. La fonction f est continue sur r privé de 1 pour a=1 ou 0, et g est continue sur r privé de 0 et 1 pour alpha, beta et gamma appartenant à l'ensemble x 1 moins x, x pour x appartenant à R.

Prolongements par continuité de fonctions cosinus et sinus

Dans cette vidéo, Paul étudie le prolongement par continuité de fonctions contenant des sinus et des cosinus. Il commence par examiner si la fonction f2x = sinx*sin(1/x) est prolongeable par continuité à R entier. En appliquant une inégalité et en montrant que la limite en 0 est bornée, il conclut que la fonction est bien prolongeable par continuité. En revanche, lorsqu'il examine la fonction g = cos(x)*cos(1/x), il constate que cette fonction ne peut être prolongeable par continuité car cos(1/x) tend vers 1 en 0, ce qui ne permet pas d'écraser les oscillations. Paul utilise la méthode de considération de deux suites qui tendent vers 0 mais dont les limites diffèrent, pour prouver que la limite de g en 0 n'existe pas. Enfin, Paul étudie la fonction h = sin(x+1)*ln(1+x) qui présente une forme indéterminée en -1. En appliquant une astuce pour ramener la limite en 0, il montre que la fonction est prolongeable par continuité. Ainsi, il conclut que h est bien prolongeable par continuité sur R.

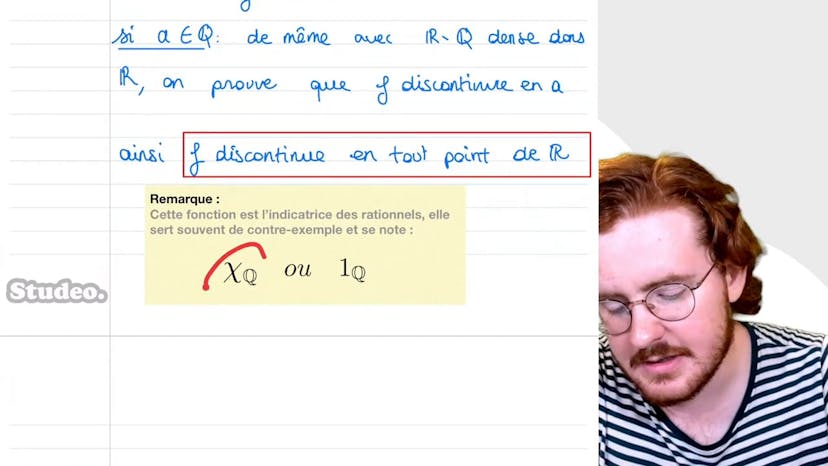
Indicatrice de Q

La fonction f de r dans R est définie par 1 si x est rationnel et 0 si x n'est pas rationnel. Il est montré que f est discontinue en tout point en utilisant la caractérisation séquentielle de la continuité. On prend un point a dans R et on montre qu'il existe une suite de réels qui tend vers a et dont la limite de f de ces réels n'est pas égale à f de a. Si a est irrationnel, on utilise le fait que R privé de q est dense dans R pour montrer la discontinuité. Cette fonction, l'indicatrice des irrationnels, est simple et sert souvent de contre-exemple sur la continuité.

Fonctions min et max

Nous apprenons dans cette vidéo que les fonctions minimum et maximum de deux fonctions continues f et g en x0 sont elles-mêmes continues en x0. Pour prouver cela, il est plus efficace de se rappeler que les expressions du minimum et du maximum peuvent être écrites visuellement en fonction de f et g, plutôt que d'utiliser la définition de la continuité ou des suites. En utilisant des formules classiques, le maximum de a et b est donné par a + b + |a - b|/2 et le minimum de a et b par a + b - |a - b|/2. Les formules correspondantes pour les fonctions minimum et maximum de f et g en x0 sont alors 1/2(f+g+|f-g|) et 1/2(f+g-|f-g|). Étant donné que f et g sont continues en x0, la différence de f et g est continue en x0 et la valeur absolue de cette différence est également continue. Ainsi, par les théorèmes généraux, les fonctions minimum et maximum de f et g en x0 sont bien continues en x0.

Équation fonctionnelle

Dans cette vidéo, Paul résout une équation fonctionnelle pour trouver les fonctions continues vérifiant que f(x+y) = f(x) + f(y). Il note que les fonctions linéaires (f(x) = ax) vérifient cette équation, et utilise la densité des rationnels pour prouver que toute fonction vérifiant cette équation est linéaire. Il prouve également que f(0) = 0 et que f(nx) = nf(x) pour tous les entiers n et x. Enfin, il montre que toute fonction vérifiant cette équation est bien une fonction linéaire.

Vitesse du courant électrique

Dans ce cours, on apprend comment déterminer la vitesse du courant électrique. Tout commence par la détermination de la densité volumique d'un atome dans le cas d'un métal, en se basant sur la taille d'un atome. Ensuite, on estime la densité volumique de charge dans un bloc de métal, en considérant que chaque atome possède un électron de valence pour la conduction du courant électrique. Enfin, pour calculer la vitesse de déplacement des porteurs de charge dans un câble de haute tension, on fait un comptage de charges qui traversent une section donnée pendant un intervalle de temps. Le résultat est surprenant, mais expliqué par la continuité d'électrons qui permet une sensation d'instantanéité.

Association de dipôles

Dans ce cours, Matisse de Studio explique comment associer des dipôles entre eux. Il commence par un circuit de trois résistances et explique comment trouver la résistance équivalente en divisant le circuit en segments et en utilisant la formule de Parker. Ensuite, il calcule la puissance dissipée par effet Joule et effectue une deuxième exercice pour un circuit de condensateurs en évaluant la capacité équivalente avant de calculer l'énergie stockée et expliquer sous quelle forme elle est stockée.

Diviseurs de tension

Dans cette vidéo, Matisse de Studio explique comment diviser une tension appliquée sur deux dipôles en série, que ce soit des résistances, des condensateurs ou des bobines. Pour cela, il utilise une célèbre formule qu'il démontre à chaque fois. Pour les résistances, la formule est U1=R1/(R1+R2)*E, pour les condensateurs, elle est U1=C2/(C1+C2)*E, et pour les bobines, elle est U1=L1/(L1+L2)*E. Il explique que la clé de l'exercice est de se ramener à ce que les dipôles ont en commun, à savoir le courant. Il utilise donc la loi d'Ohm et des schémas équivalents pour relier les courants et les tensions des différents dipôles. Cette méthode est applicable à de nombreux cas pratiques en électricité.

Diviseurs de courant

Dans cette vidéo, Matisse de Studio explique comment diviser des courants dans des circuits électriques. Il utilise des exemples avec des résistances, des condensateurs et des bobines. Pour le premier cas, il démontre que le courant qui traverse la résistance R1 est égal à R2 sur R1 plus R2 fois le courant total I. Pour le deuxième cas, il montre que le courant qui passe à travers le condensateur 1 est égal à C1 sur C1 plus C2 fois le courant total I. Enfin, pour les bobines, il montre que le courant qui traverse la première bobine est égal à L2 sur L1 plus L2 fois le courant total I. Ces relations sont importantes pour l'étude cinétique des circuits électriques.

Transformation Thévenin-Norton

Dans ce cours, on apprend comment résoudre un circuit électrique en utilisant les associations de résistances et le diviseur de tension pour déterminer la tension et le courant. On nous présente également la transformation de Thevenin-Norton qui consiste à remplacer un générateur avec une résistance en série par un générateur de courant mis en dérivation avec cette résistance. On applique ensuite le diviseur de courant pour résoudre le circuit. Les deux méthodes peuvent être utilisées en fonction de la préférence et de la familiarité de l'étudiant avec les associations de résistances. Finalement, deux expressions sont obtenues pour la tension et le courant en fonction des grandeurs du circuit.

RC série

Dans cette vidéo, Matisse de Studio étudie le circuit RC série. Le circuit est composé d'un générateur de tension continue, d'une résistance et d'un condensateur. L'objectif est d'établir l'équation différentielle vérifiée par la tension au bord du condensateur (UC). Pour cela, Matisse utilise la loi des mailles qui indique que UC + RI = E. Il remplace ensuite le courant (I) par C * dUC/dt, où C est la capacité du condensateur. En simplifiant l'expression, il obtient l'équation différentielle : dUC/dt + (1/RC) * UC = E/(RC). Pour résoudre cette équation, Matisse détermine les conditions initiales. Le condensateur est initialement déchargé, ce qui signifie que UC(0-) = 0. Il utilise ensuite cette condition de continuité pour déterminer la constante dans la solution générale de l'équation homogène. Ensuite, Matisse cherche une solution particulière en supposant que la tension est constante par rapport au temps. Il trouve que la tension associée est E. En sommant la solution générale et la solution particulière, il obtient la solution globale de l'équation différentielle : UC(t) = E * (1 - exp(-t/RC)). Matisse représente graphiquement cette solution, montrant qu'elle augmente exponentiellement et tend vers E lorsque t tend vers l'infini. Il calcule également la dérivée de UC par rapport au temps en t = 0, qui vaut E/(RC). Enfin, Matisse effectue une étude énergétique du circuit. Il montre que l'énergie accumulée dans le condensateur au cours de l'évolution du régime vaut 1.5 * C * E^2. De plus, l'énergie dissipée par l'effet joule dans la résistance est également de 1.5 * C * E^2. Ainsi, la somme de l'énergie accumulée et dissipée égale l'énergie fournie par le générateur. En conclusion, cette vidéo donne une étude complète du circuit RC série, en expliquant les étapes pour établir l'équation différentielle, résoudre celle-ci et effectuer une étude énergétique.