Cours d'apprentissage en ligne

Analyse

Suites complexes

Dans cette méthodologie, nous étudierons les suites récurrentes d'Ordre 2 et en particulier leurs solutions complexes. Cela peut être utile non seulement dans des exercices spécifiques, mais également dans d'autres types d'exercices. Tout d'abord, nous cherchons les solutions complexes d'une équation de suite spécifique, où nous voulons que notre suite satisfasse à une certaine condition. Nous résolvons d'abord l'équation sans tenir compte de cette condition. Ensuite, nous recherchons une solution particulière qui satisfera à la condition donnée. Si une solution particulière est trouvée, nous combinons cette solution avec la solution homogène pour obtenir l'ensemble complet des solutions. Cette méthode nécessite de résoudre des équations et de manipuler des polynômes. Si vous ne comprenez pas encore ce concept, ne vous inquiétez pas, vous le verrez bientôt dans le prochain chapitre.

Exercice 1 (QCM : Suites et fonctions)

Aucun résumé n'est disponible pour cette vidéo

Exercice 2 (Géométrie 3D)

Aucun résumé n'est disponible pour cette vidéo

Exercice 3 (Probabilités)

Aucun résumé n'est disponible pour cette vidéo

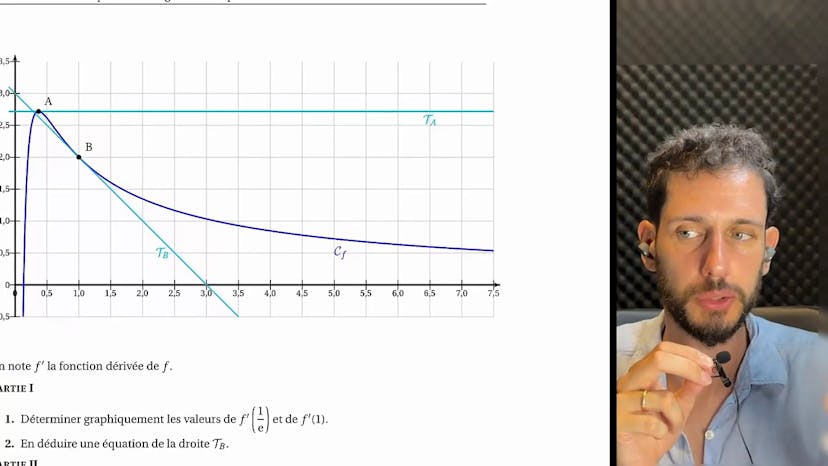
Exercice A (Logarithme et convexité)

L'exercice consiste à analyser graphiquement une fonction dérivable, définie sur l'intervalle (0,+∞), et représentée par une courbe dans un repère. On note A et B les points d'intersection de la courbe avec l'axe des abscisses, et on observe que la tangente en A est parallèle à cet axe

Écriture ensembliste

Dans cet exercice, nous avons trois événements A, B et C provenant de l'univers Omega. Nous devons les traduire en langage ensembliste en utilisant les symboles d'intersection, d'union et le complémentaire. Voici les résumés en langage SEO-friendly : 1. Seul A se réalise : A ∩ (B̅ ∩ C̅) ou A ∩ (B ∪ C̅) 2. A et B se réalisent, mais pas C : A ∩ B ∩ C̅ 3. Les trois événements se réalisent : A ∩ B ∩ C 4. Au moins l'un des trois événements se réalise : A ∪ B ∪ C 5. Au moins deux des trois événements se réalisent : (A ∩ B) ∪ (A ∩ C) ∪ (B ∩ C) 6. Aucun ne se réalise : A̅ ∩ B̅ ∩ C̅ 7. Au plus l'un des trois se réalise : Ω̅ \ (A ∪ B ∪ C) 8. Exactement deux des trois se réalisent : (A ∩ B) ∪ (A ∩ C) ∪ (B ∩ C) ∩ (A̅ ∪ B̅ ∪ C̅)

Probabilité de l’intersection

Dans cet exercice, nous cherchons à démontrer l'inégalité de la probabilité de l'intersection de deux événements. Selon la formule, la probabilité de l'intersection est comprise entre le maximum de 0 et la somme des probabilités des deux événements moins 1, et le minimum des probabilités de chaque événement. Pour démontrer le côté droit de l'inégalité, nous utilisons la formule et montrons que la probabilité de l'union de deux événements est plus grande que la probabilité de chaque événement individuellement. En remplaçant les valeurs, nous constatons que la probabilité de l'intersection est plus petite que la probabilité de chaque événement individuel et donc plus petite que le minimum des deux. Ensuite, nous démontrons l'égalité de l'autre sens en montrant que la probabilité de l'intersection est plus grande que le maximum des deux probabilités individuelles. Nous prouvons que la probabilité de l'intersection est plus grande que zéro en tant que probabilité, et en utilisant la formule, nous montrons qu'elle est également plus grande que le maximum des deux probabilités individuelles. En conclusion, cet exercice démontre l'inégalité de la probabilité de l'intersection de deux événements en utilisant des formules et des comparaisons de probabilités.

Inégalité de Bonferroni

Dans cet exercice, nous voulons démontrer la formule suivante en utilisant la récurrence : la probabilité de l'intersection de n événements est supérieure ou égale à la somme des probabilités moins n moins 1. Nous commençons par l'initialisation pour n égal à 2. La probabilité de l'intersection est égale à la probabilité de A1 plus la probabilité de A2 moins la probabilité de leur union, soit P(A1) + P(A2) - P(A1 ∪ A2) = P(A1) + P(A2) - 1. Nous obtenons bien moins 1 ici. Ensuite, nous passons à l'hérédité. La probabilité de l'intersection jusqu'à n plus 1 est égale à la probabilité de l'intersection jusqu'à n fois la probabilité de n plus 1 moins la probabilité de l'intersection avec A n plus 1. Nous utilisons la formule P(A ∪ B) = P(A) + P(B) - P(A ∩ B) que nous connaissons depuis longtemps. Notre hypothèse de récurrence nous dit que cette probabilité est supérieure ou égale à la somme des P(Ai) moins n moins 1. Nous réinjectons ensuite P(An+1) dans la somme, sachant que cette probabilité est plus petite que 1. Comme il y a un moins, le plus grand, cela nous convient parfaitement. Nous réinjectons cette probabilité dans la somme jusqu'à n plus 1 et nous obtenons moins n plus 1, le moins 1 ici, qui correspond à n plus 1 moins 1 dans la formule. L'hérédité est démontrée et la récurrence a été relativement rapide à faire. Nous avons bien obtenu la formule demandée. C'est tout pour cet exercice.

Loi de dés pipés

Dans cet exercice, on cherche à modéliser une expérience aléatoire avec un dé à six faces, où la probabilité d'obtenir une face est proportionnelle au chiffre sur cette face. Pour cela, on a défini un espace probabilisé où la probabilité de faire 1 est x, la probabilité de faire 2 est 2x, et ainsi de suite jusqu'à la probabilité de faire 6 qui est 6x, pour que les probabilités soient proportionnelles. On sait que la somme des probabilités de toutes les faces doit être égale à 1. Donc on a l'équation x + 2x + 3x + 4x + 5x + 6x = 1, ce qui donne 21x = 1, et donc x = 1/21. Maintenant, on veut calculer la probabilité d'obtenir un chiffre pair. Comme les événements sont disjoints, on peut simplement faire la somme des probabilités des faces paires, qui sont 2/21 + 4/21 + 6/21. En simplifiant par 3, on obtient 4/27. Ensuite, on reprend les questions en modifiant le dé à six faces pour que la probabilité d'obtenir une face paire soit le double de la probabilité d'obtenir une face impaire. On a donc x pour les faces impaires et 2x pour les faces paires. En utilisant la même méthode, on obtient x = 1/9 et les probabilités des faces paires sont 2/9 + 2/9 + 2/9, ce qui simplifie à 2/3.

Déterminer une loi

Dans cet exercice, on part de l'ensemble de nombres 1 à n et on cherche à trouver une probabilité proportionnelle à k² pour avoir l'ensemble 1 à k. On utilise la variable λ pour représenter cette probabilité et on sait que la probabilité d'avoir juste k est égale à λk² moins λ(k-1)². Après développement, on obtient 2λk-1 comme probabilité d'avoir juste k. On sait également que la probabilité d'avoir tout l'ensemble de 1 à n est égale à 1. En utilisant cette information, on peut déduire que λ est égal à 1/n². Ainsi, la probabilité d'avoir juste k parmi les nombres 1 à n est égale à (2k-1)/n². Voilà en résumé l'exercice.

Jeu de cartes

Dans cet exercice de ProBas, nous avons tiré simultanément 3 cartes au hasard dans un paquet de 32 cartes. La première question était de déterminer la probabilité d'obtenir uniquement des cœurs. Il y a 8 cœurs dans un jeu de 32 cartes, donc le nombre de tirages possibles pour avoir uniquement des cœurs est de 3 parmi 8. Le nombre total de tirages est de 3 parmi 32. En utilisant le concept d'équiprobabilité, la probabilité recherchée est le nombre d'issues favorables (3 parmi 8) divisé par le nombre d'issues totales (3 parmi 32), soit 7 sur 620. Ensuite, nous avons calculé la probabilité d'obtenir uniquement des As. Le nombre de tirages possibles pour avoir uniquement des As est de 3 parmi 4. Le nombre total de tirages est de 3 parmi 32. En effectuant le même raisonnement, la probabilité recherchée est 1 sur 1240. Enfin, nous avons abordé la dernière question : la probabilité d'obtenir 2 cœurs et 1 pic. Pour cela, nous avons calculé séparément le nombre de tirages possibles pour avoir 2 cœurs (2 parmi 8) et pour avoir 1 pic (1 parmi 8). En multipliant ces deux nombres, nous avons obtenu 7 fois 4 fois 8. Le nombre total de tirages était de 3 parmi 32, soit 32 fois 31 fois 30. En simplifiant les calculs, nous avons trouvé que la probabilité recherchée est de 7 sur 155. Voilà pour cet exercice.