Cours d'apprentissage en ligne

La planète mercure

Dans cet exercice, nous étudions la planète Mercure et la sonde Messenger. La première partie concerne la trajectoire de Mercure et nous rappelle la première loi de Kepler, selon laquelle l'orbite de chaque planète est une ellipse dont un des foyers est le Soleil. Nous devons calculer le demi-grand axe de l'orbite de Mercure, en utilisant les informations fournies sur la distance au Soleil (0,31 à 0,47 UA). Ensuite, nous devons appliquer la deuxième loi de Kepler, selon laquelle une planète balaie des aires égales pendant des durées égales. Nous devons déterminer dans quelle partie de sa trajectoire Venus atteint la vitesse de 39 km par seconde. Nous pouvons le déterminer en observant la taille des aires balayées par Mercure à différents endroits de son orbite. Enfin, nous examinons la trajectoire de la sonde Messenger autour de Mercure. Nous devons appliquer le principe fondamental de la dynamique en utilisant l'expression de la force gravitationnelle et les données fournies sur la période de révolution de la sonde (8 heures) et l'altitude au plus près de la surface (200 km). Nous pouvons ensuite isoler la masse de Mercure en utilisant l'accélération mesurée. En appliquant les lois de Kepler au mouvement de la sonde Messenger, nous pouvons calculer la valeur du demi-grand axe de l'orbite et comparer cela à la réalité. Nous constatons que la trajectoire de la sonde n'est pas circulaire, ce qui explique pourquoi le demi-grand axe est plus grand que la somme du rayon de Mercure et de l'altitude de la sonde. Cet exercice nous permet d'étudier la gravitation, les lois de Kepler et le principe fondamental de la dynamique.

Nos oreilles, on y tient !

Dans ce cours, Layla aborde un exercice d'acoustique portant sur l'audition et les niveaux sonores. Elle utilise les formules liées aux décibels pour analyser si certaines activités peuvent être nocives pour l'audition. Layla explique que le niveau d'intensité sonore est exprimé en décibels, allant jusqu'à 120 dB, et que la limite de nocivité est située au-dessus de 85 décibels. Elle utilise la formule L = log(I/I0) pour étudier différentes situations et déterminer si le niveau sonore est nuisible pour la santé. Dans la première situation, Layla décrit deux conducteurs séparés par une distance D2, avec un autoradio dans la première voiture. Les deux véhicules ont les fenêtres baissées. Layla utilise le modèle géométrique d'atténuation sonore pour expliquer que plus on est loin de la source sonore, plus l'intensité sonore est faible. Elle utilise ensuite les formules pour calculer l'intensité sonore reçue par le conducteur 1 (I1) en fonction de la puissance sonore (P) et des distances D1 et D2. Elle explique également comment calculer l'atténuation géométrique entre les deux conducteurs (AGO) en utilisant les niveaux sonores mesurés. Layla passe ensuite à l'analyse expérimentale de la situation, où les conducteurs mesurent les niveaux sonores avec un sonomètre. Elle explique comment calculer l'atténuation expérimentale à partir des niveaux mesurés (L1 et L2) en utilisant la formule L1 - L2. Dans la deuxième partie, Layla étudie ce qui se produit lorsque les fenêtres des voitures sont fermées. Elle explique que cela entraîne une atténuation supplémentaire due à l'absorption du son par les vitres. Elle utilise les formules pour calculer cette atténuation supplémentaire en ajoutant l'atténuation géométrique (AGO) à l'atténuation due aux fenêtres (Afenêtre). Layla compare ensuite le niveau sonore mesuré par le conducteur 1 avec la limite de nocivité pour déterminer si le conducteur est exposé à un niveau sonore dangereux. En résumé, ce cours aborde l'atténuation sonore et analyse différentes situations pour déterminer si les niveaux sonores sont nocifs pour l'audition. Layla utilise des formules et des calculs pour étudier l'atténuation géométrique et l'atténuation due aux fenêtres des voitures.

La vitamine C sans sucre (1)

Dans cette vidéo, Théobald de Cidéo explique comment déterminer le spectre infrarouge de l'aspartame, une molécule que l'on retrouve dans la vitamine C. Il commence par donner des informations sur la vitamine C et sur l'aspartame, qui est un édulcorant de synthèse utilisé dans de nombreux produits. Ensuite, il aborde les différentes familles fonctionnelles présentes dans la formule topologique de l'aspartame. Il montre que l'aspartame contient un acide carboxylique, un amine et un ester, et explique l'importance de ces groupes pour l'analyse du spectre infrarouge. Il explique ensuite que l'aspartame peut être synthétisé à partir de l'acide aspartique, et demande de représenter la formule semi-développée de cet acide. Il souligne l'importance de respecter la géométrie de la molécule et de dessiner les liaisons entre les bons éléments. Enfin, il présente les spectres obtenus par spectroscopie infrarouge de l'aspartame et de l'acide aspartique, sans préciser à quel spectre correspond quelle molécule. Il explique les bandes caractéristiques qui devraient ressortir dans le spectre infrarouge de l'aspartame, en se basant sur les différentes familles fonctionnelles présentes. Il analyse ensuite les spectres infrarouges des deux molécules et conclut que le spectre 2 correspond au spectre de l'aspartame, car il présente toutes les bandes caractéristiques attendues. Enfin, il termine en invitant les spectateurs à poser des questions en commentaire et annonce une prochaine vidéo.

La vitamine C sans sucre (2)

Dans cette vidéo, Théobald de Studio aborde le sujet de l'aspartame et sa synthèse. Il explique que l'aspartame est une molécule présente dans la vitamine C et qu'il souhaite montrer comment la synthétiser. Il commence par présenter le contexte de l'exercice, qui tourne autour de la vitamine C et de l'acide ascorbique qui la compose. Il mentionne également que la synthèse de l'aspartame nécessite plusieurs étapes, mais qu'il se concentrera sur l'une des premières étapes consistant à transformer une espèce chimique A en une espèce chimique C. Il explique ensuite qu'il y a trois protocoles expérimentaux, notés 1, 2 et 3, qui sont réalisés à la même température. Ces protocoles varient en termes de masses des réactifs, de rendements, etc. La première question de l'exercice demande de déterminer le volume de réactif B liquide à prélever dans le protocole 1. Théobald explique qu'il peut utiliser la quantité de matière du réactif B (NB) donnée dans l'énoncé pour calculer le volume correspondant. Il utilise la formule du volume (massse/masse volumique) pour obtenir le résultat, qui est de 1,0 millilitre. 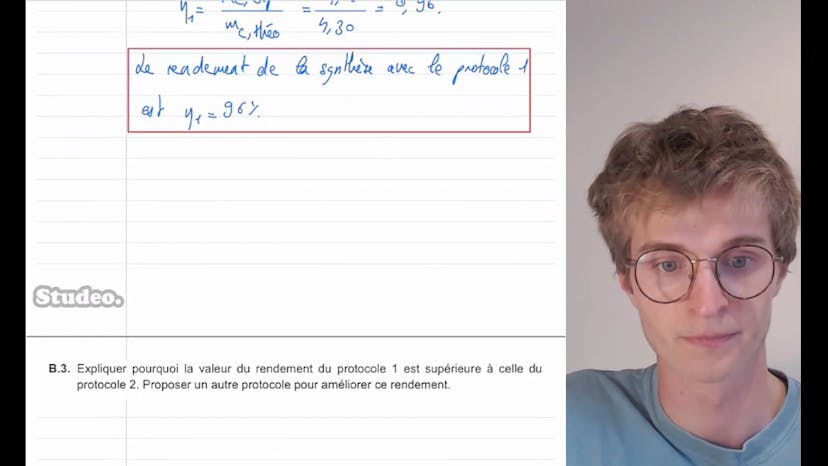Ensuite, il est demandé de calculer le rendement de la synthèse dans le protocole 1. Théobald explique que le rendement est défini comme la masse du produit C obtenue expérimentalement divisée par la masse théorique maximale du produit. Il utilise les données expérimentales pour obtenir la masse théorique en supposant une réaction totale. Il obtient un résultat de 4,30 grammes de produit C théoriquement obtenu. En comparant cela avec la masse expérimentale de 4,12 grammes, il calcule un rendement de 96% dans le protocole 1. On lui demande ensuite d'expliquer pourquoi le rendement du protocole 1 est supérieur à celui du protocole 2. Théobald remarque que la seule différence entre les deux protocoles est la quantité de matière en réactif A, qui est plus élevée dans le protocole 1. Il explique que cela signifie que A est en excès dans le protocole 1, ce qui permet d'obtenir un rendement plus élevé. Il suggère également que l'élimination d'un des produits, comme l'eau, pourrait améliorer le rendement. En utilisant les informations du tableau, Théobald identifie ensuite le rôle du palladium sur carbone. Il remarque que sa présence dans les deux premières réactions raccourcit la durée de réaction, ce qui indique que le palladium sur carbone agit comme un catalyseur, accélérant la réaction. En conclusion, Théobald résume les résultats obtenus dans cette vidéo et annonce qu'il abordera la partie C de l'exercice dans une prochaine vidéo. Il encourage les spectateurs à poser leurs questions dans les commentaires.

La vitamine C sans sucre (3)

Dans cette vidéo, Théobald de Cidéo explique l'acide ascorbique, qui est le nom scientifique de la vitamine C. Il aborde un exercice du BAC portant sur l'acide ascorbique. Dans cet exercice, il est demandé de calculer la concentration en quantité de matière de l'acide ascorbique dans une solution obtenue en dissolvant un comprimé de 0,50 g d'acide ascorbique dans 200,0 ml d'eau. Théobald utilise la formule de concentration en quantité de matière qui est le nombre de moles divisé par le volume de la solution. Il calcule ensuite la concentration en quantité de matière de l'acide ascorbique, qui est de 1,4 x 10^-2 mol/L, correspondant à la réponse B. Ensuite, Théobald explique comment écrire l'équation de réaction entre l'acide ascorbique et l'eau, en soulignant que l'acide ascorbique est un acide faible. Il présente les couples d'espèces présentes dans la réaction, et montre que la réaction se produit entre l'acide ascorbique et l'eau pour former l'ion ascorbate et l'ion H3O+. Il mentionne également que le pH à l'équilibre de la solution est de 2,9. Théobald aborde ensuite le calcul de la constante d'acidité Ka, en montrant comment caractériser l'équilibre à l'aide d'un tableau d'avancement. Il utilise les concentrations en ion aspartame et en ion H3O+ pour déterminer la valeur de Ka, qui peut s'écrire selon la formule donnée dans l'énoncé. L'étape suivante consiste à trouver la valeur de Ka et le pKa du couple acide ascorbique-ion ascorbate. Théobald substitue la concentration en ion H3O+ par C standard multipliée par 10^-pH dans la formule de Ka, et obtient une valeur de Ka égale à 1,2 x 10^-4. Il calcule ensuite le pKa, qui est égal à 3,9. Enfin, Théobald représente le diagramme de prédominance du couple ascorbique-ion ascorbate en fonction du pH. Il indique que la forme majoritaire dans l'estomac, où le pH est d'environ 2, est l'acide ascorbique, car l'acide prédomine à pH faible. Il conclut la vidéo en souhaitant bonne chance dans les révisions et en proposant de poser des questions en commentaire.

La vitamine C sans sucre (4)

Dans cette vidéo, Théoval de Cedéo aborde le sujet de la détermination de la masse d'acide ascorbique contenu dans un comprimé de vitamine C. Le fabricant indique que chaque comprimé contient 500mg de vitamine C, uniquement sous forme d'acide ascorbique. L'objectif est de vérifier cette information en utilisant une méthode de titrage conductimétrique. Le processus expérimental consiste à dissoudre un comprimé de vitamine C dans de l'eau distillée pour obtenir une solution d'un volume de 250mL. Ensuite, un échantillon de 40mL de cette solution est titré à l'aide d'une solution d'hydroxyde de sodium de concentration connue. L'équation de réaction du titrage est donnée, où l'acide ascorbique réagit avec les ions hydroxyde. Le dispositif expérimental est simple : un bécher contenant la solution titrée avec une sonde de conductimétrie reliée à un conductimètre et une burette graduée contenant la solution d'hydroxyde de sodium. Les courbes d'évolution de la conductivité du milieu réactionnel en fonction du volume d'hydroxyde de sodium versé sont données. On observe une augmentation de la conductivité avec l'augmentation du volume ajouté, avec deux demi-droites tracées. Pour expliquer cette évolution, il est nécessaire de comprendre la présence des ions dans la solution. Avant l'équivalence, les ions hydroxyde réagissent avec l'acide ascorbique, tandis que les ions sodium restent inchangés. Après l'équivalence, les ions hydroxyde sont ajoutés mais ne réagissent plus avec l'acide ascorbique, tandis que les ions sodium restent inchangés. Cette évolution explique l'augmentation de la conductivité avant et après l'équivalence. La concentration molaire d'acide ascorbique de la solution titrée est déterminée en utilisant le principe de l'équivalence. Le volume à l'équivalence est trouvé à partir de l'intersection des deux demi-droites tracées sur la courbe. En utilisant cette concentration et le volume de la solution S, la quantité de matière d'acide ascorbique est calculée et convertie en masse. La masse d'acide ascorbique contenue dans un comprimé est trouvée être de 0,19g. En comparant cette valeur à celle annoncée par le fabricant (200mg), on calcule le rapport entre la valeur mesurée et la valeur de référence. Ce rapport, également appelé z-score, est égal à 1, ce qui indique que la mesure est compatible avec la valeur de référence. En conclusion, la méthode de titrage conductimétrique a permis de déterminer avec précision la masse d'acide ascorbique dans un comprimé de vitamine C, et cette valeur est cohérente avec celle annoncée par le fabricant.

La pente d'eau de Montech (1)

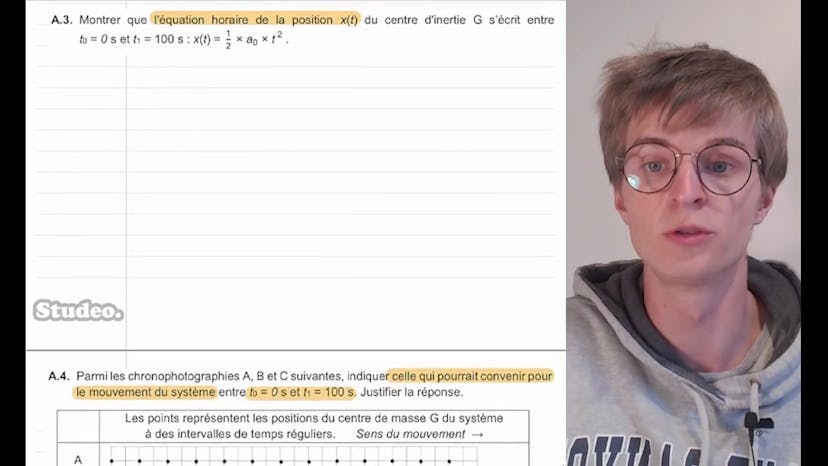
Avoir un ascenseur à bateau est très avantageux pour monter ou descendre les bateaux rapidement. L'ascenseur à bateau de Montaigue est un exemple de cela. Il est devenu un site touristique depuis 2021. Le principe de fonctionnement de cet ascenseur à bateau est expliqué ici. Il utilise une automotrice pour pousser le masque, le bateau et l'eau qui est entre les deux, permettant ainsi au système de monter la pente. Dans cette première partie, nous étudions le mouvement de ce système. Le centre de masse G se déplace selon l'axe OX avec un angle α par rapport à l'horizontale. À l'instant initial t=0, le centre de masse est au point O. Nous utilisons une chronophotographie pour représenter ce mouvement. On nous demande de donner la relation entre l'accélération et la vitesse, et de déduire la relation entre leurs valeurs absolues. La relation entre l'accélération A de t et la vitesse V de t est donnée par la dérivée de la vitesse par rapport au temps. En raison du mouvement rectiligne, nous pouvons exprimer l'accélération et la vitesse en termes de leurs valeurs absolues. Donc, A de t est égal à la dérivée de la vitesse par rapport au temps. Nous devons ensuite montrer que l'accélération du système est constante entre t=0 et t1=100 secondes, et qu'elle vaut A0=1,20 fois 10 à la puissance -2 m/s². En analysant la courbe, nous pouvons voir que l'accélération est constante dans cette période. En utilisant la relation delta V/delta t, nous pouvons calculer la valeur de l'accélération. Delta V est égal à V(t1) - V(t0) et delta t est égal à t1 - t0. En utilisant les conditions initiales V(t0) = 0 et t0 = 0, nous obtenons A0 = 1,20 fois 10 à la puissance -2 m/s², la valeur donnée dans l'énoncé. Ensuite, nous devons trouver l'équation de la vitesse et de la position du centre de masse du système en fonction de A0 et de t pour cette partie du mouvement. En intégrant l'accélération, nous obtenons la vitesse, V(t) = A0t. En intégrant à nouveau la vitesse, nous obtenons la position du centre de masse, x(t) = 1,5A0t². Entre t=0 et t1=100 secondes, la vitesse est une ligne droite et la position est une courbe parabolique. Enfin, en utilisant des chronophotographies, nous devons déterminer quelle représentation du mouvement correspond à notre système entre t0 et t1. En utilisant les équations précédentes, nous pouvons calculer les positions des points à différents intervalles de temps. En comparant ces positions avec celles des chronophotographies A, B et C, nous pouvons déterminer laquelle correspond à notre mouvement. La chronophotographie B correspond à notre mouvement car les distances entre les points sont régulières pour des intervalles de temps réguliers, ce qui correspond à une accélération constante.

La pente d'eau de Montech (2)

Dans cette vidéo, Théobald poursuit l'exercice sur l'ascenseur à bateau. Dans la première partie, il étudie la dynamique du système, tandis que dans la deuxième partie, il utilise une lunette pour observer le bateau. Le système étudié est composé du bateau, de l'eau et du masque. Le bateau se déplace le long de la pente et est soumis à quatre forces : son poids, la réaction normale de la pente, les forces automotrices et la force de frottement du masque et de l'eau le long de la pente. Les forces automotrices permettent au bateau de remonter la pente. Théobald explique que la somme des forces extérieures doit être selon le sens de l'accélération du système, qui est positif selon l'axe plus ux. Il analyse ensuite deux schémas pour déterminer lequel représente le mieux la situation. Il conclut que le schéma 1 est le plus approprié, car la somme des

Observation de la planète Mars (1)

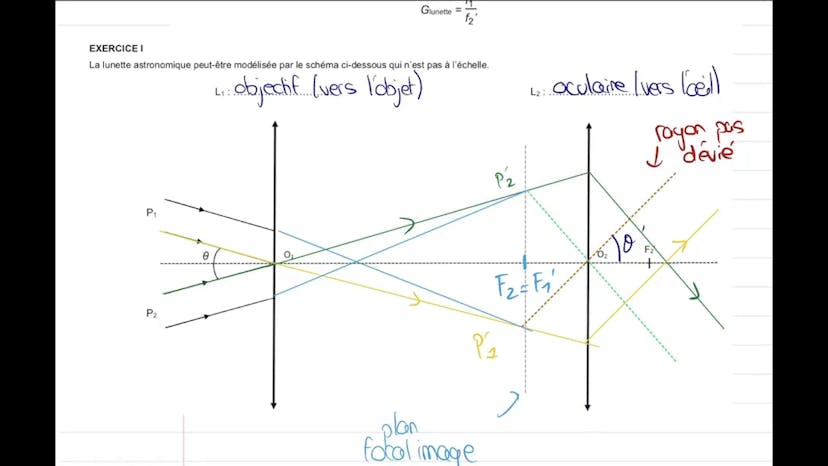
Dans cette vidéo, nous nous intéressons à l'exercice 1 d'un sujet sur l'observation de la planète Mars. Cet exercice porte sur l'optique d'une lunette astronomique en utilisant des rayons lumineux. Tout d'abord, nous devons identifier sur le schéma les lentilles qui jouent le rôle de l'objectif et de l'oculaire. Ensuite, nous apprenons que la lunette astronomique est affocale, ce qui signifie qu'elle renvoie une image à l'infini d'un objet situé à l'infini. Cela permet de ne pas fatiguer les muscles des yeux. Nous devons également tracer les rayons lumineux et expliquer pourquoi l'observateur ne voit qu'un point lumineux lorsqu'il regarde Mars à l'œil nu. Cela est dû au pouvoir de résolution de l'œil, qui détermine l'angle au-delà duquel l'œil distingue deux points séparés. Si cet angle est plus petit que l'angle de vision de l'observateur, il ne pourra pas distinguer les deux points. En utilisant la lunette astronomique, l'observateur voit un disque lumineux où il peut distinguer le haut et le bas de Mars. Cela est dû au grossissement de la lunette, qui permet de mieux résoudre le système. En résumé, cet exercice aborde l'utilisation de la lunette astronomique pour observer la planète Mars, en se concentrant sur l'optique et le pouvoir de résolution de l'œil.

Observation de la planète Mars (2)

Dans cette vidéo, Laila de STUDIO explique comment déterminer le diamètre de la planète Mars à partir des mesures d'angle obtenues à travers une lunette astronomique. Elle commence par présenter les données disponibles, telles que les angles θ1 et θ2 mesurés aux points A et B, ainsi que la distance Soleil-Mars. En analysant le schéma, elle déduit que θ1 correspond à θA et θ2 correspond à θB, puis elle utilise la trigonométrie pour établir l'expression du diamètre dm de Mars en fonction de θA et θB. Dans la figure 2, elle observe que la distance D1 + D2 est égale à deux fois la distance Soleil-Mars, ce qui lui permet d'exprimer dm en fonction de cette distance. En effectuant un calcul numérique, elle trouve que le diamètre de Mars est de 6,8 x 10^3 km. Cette valeur est proche du diamètre moyen de référence, ce qui confirme l'efficacité de la méthode utilisée. Elle conclut en indiquant qu'elle abordera la dernière partie de l'exercice dans une prochaine vidéo.

Observation de la planète Mars (3)

Aujourd'hui, Layla de STUDIO termine l'exercice 1 du sujet de bac sur l'observation de la planète Mars. Les deux premières parties ont porté sur l'étude de Mars du point de vue optique, en utilisant une lunette astronomique pour déduire son diamètre. Dans cette dernière partie, on passe à la mécanique et on cherche à déterminer la masse de Mars en observant le satellite Phobos et en utilisant les lois de Newton. Le satellite est soumis uniquement à la gravité de Mars. Pour déterminer la vitesse de Phobos sur son orbite circulaire, on utilise la seconde loi de Newton et le repère de Freinet. Grâce à la formule de l'accélération dans ce repère, on trouve que la vitesse de Phobos est égale à la racine de gm/rmp, où gm est la constante gravitationnelle de Mars et rmp le rayon de l'orbite de Phobos. Ensuite, pour déterminer la masse de Mars, on utilise une méthode ouverte. On peut utiliser les valeurs connues de la période de révolution de Phobos et du rayon de son orbite, ainsi que la relation entre la vitesse et la masse de Mars que l'on vient de trouver. En résolvant les équations, on trouve que la masse de Mars est d'environ 464 fois 10^23 kg, ce qui est cohérent avec l'information donnée selon laquelle la masse de Mars est environ dix fois moins grande que celle de la Terre.