 All subjects
All subjects
 All subjects
All subjects
Maths
Algèbre
MPSI/PCSI
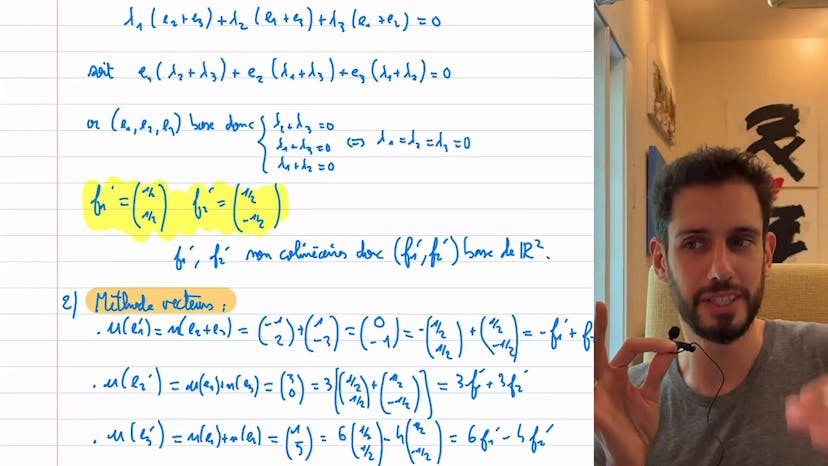
Changement de base
Dans ce cours, nous étudions une application linéaire de R3 dans R2. Nous voulons montrer que les bases E1', E2', E3' et F1', F2' sont libre pour R3 et R2 respectivement. Afin de montrer la liberté de ces vecteurs, nous les combinons de manière appropriée pour prouver que les coefficients correspondants sont nuls. De plus, nous montrons que F1' et F2' sont indépendants puisqu'ils ne sont pas collinaires. Ensuite, nous cherchons la matrice de l'application linéaire U dans ces nouvelles bases. Pour cela, nous exprimons U(E1'), U(E2'), et U(E3') en termes de F1' et F2'. En utilisant la définition de U dans la base canonique, nous calculons ces expressions dans la base canonique avant de les réécrire dans la base F1, F2. Ensuite, nous essayons différentes combinaisons linéaires de F1' et F2' pour exprimer les résultats dans la base F1', F2'. En résolvant un système ou en faisant des essais, nous trouvons les coefficients appropriés. Finalement, nous obtenons la matrice de U dans les nouvelles bases en utilisant les expressions trouvées. Il est recommandé de faire ces calculs mentalement, mais il est également possible de poser des systèmes d'équations pour obtenir les coefficients.
Maths
Algèbre
MPSI/PCSI

Matrices semblables
Ce cours explique comment déterminer si les matrices A, B, C et D sont semblables. Plutôt que de tenter de trouver une matrice P telle que B = P-1 A P, on utilise l'application linéaire associée, notée F. On cherche une base (E1, E2, E3) telle que F(E1) = 0, F(E2) = E3 et F(E3) = 0. On peut réorganiser la base si nécessaire. Par exemple, pour la matrice B, on peut observer F dans la base (E2, E3, E1) au lieu de (E1, E2, E3). On choisit alors U1 = E1, U2 = E3 et U3 = E2. On vérifie que F(U1) = 0, F(U2) = E2 et F(U3) = 0, ce qui correspond bien à la matrice B. Les mêmes étapes sont appliquées pour les matrices C et D. Pour C, on choisit la base (V2, V3, V1) avec V1 = E2, V2 = E3 et V3 = E1. Pour D, on choisit la base (W2, W3, W1) avec W1 = 4E3, W2 = E2 et W3 = E1. Ainsi, en comprenant les matrices comme représentant des applications linéaires, on peut déterminer si elles sont semblables en utilisant cette méthode.
Maths
Algèbre
MPSI/PCSI

Matrice de passage
Le cours traite de l'endormorphisme U défini à partir d'une base canonique et de trois vecteurs w1, w2, w3. La matrice de cet endomorphisme est calculée en fonction de ces vecteurs. Ensuite, le cours aborde la détermination d'une base du noyau et de l'image de U, ainsi que la détermination du noyau et de l'image de l'endomorphisme U - Id, où Id est l'identité. Il est démontré que U - Id est bijective, ce qui le qualifie d'automorphisme. Enfin, le cours conclut que le noyau de cet automorphisme est réduit à zéro, ce qui signifie qu'il est inversible.
Maths
Algèbre
MPSI/PCSI
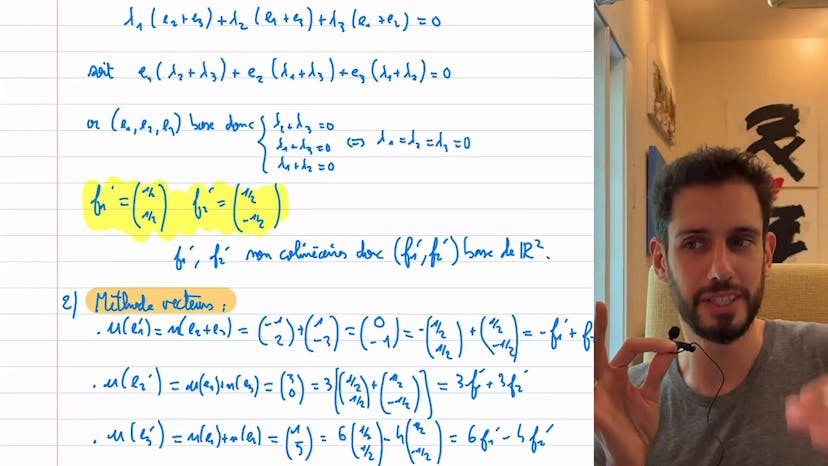
Changement de base
Aucun résumé n'est disponible pour cette vidéo
Maths
Algèbre
MPSI/PCSI

Matrices triangulaires
Ce cours traite de deux résultats sur les matrices triangulaires.
Le premier résultat démontre que pour qu'une matrice triangulaire supérieure soit inversible, tous ses coefficients diagonaux doivent être non-nuls.
Le deuxième résultat montre que toute matrice triangulaire supérieure peut être rendue semblable à une matrice triangulaire inférieure.
Pour démontrer ces résultats, l'auteur utilise des méthodes de contraposée et de changement de base. Il explique en détail les étapes à suivre pour parvenir à ces conclusions.
En utilisant des termes simples et des exemples concrets, l'auteur rend le cours facile à comprendre. Ce cours est une transcription d'une vidéo d'enseignement.
Maths Approfondies
Algèbre
ECG
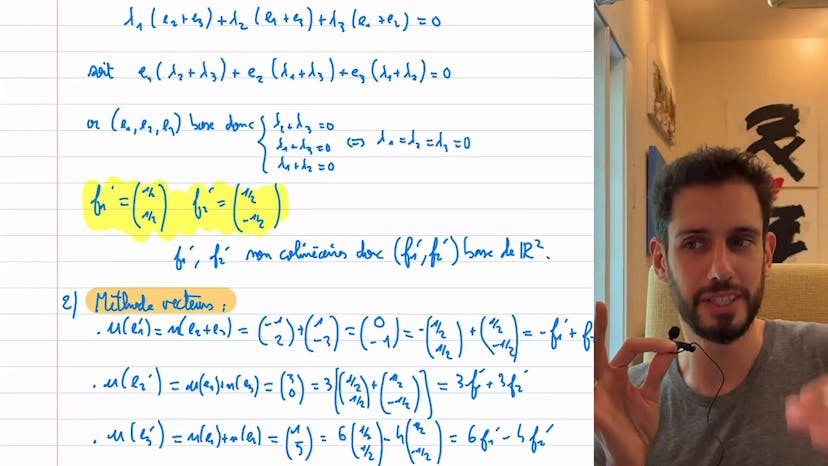
Changement de base
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG

Matrices semblables
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG

Matrice de passage
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG
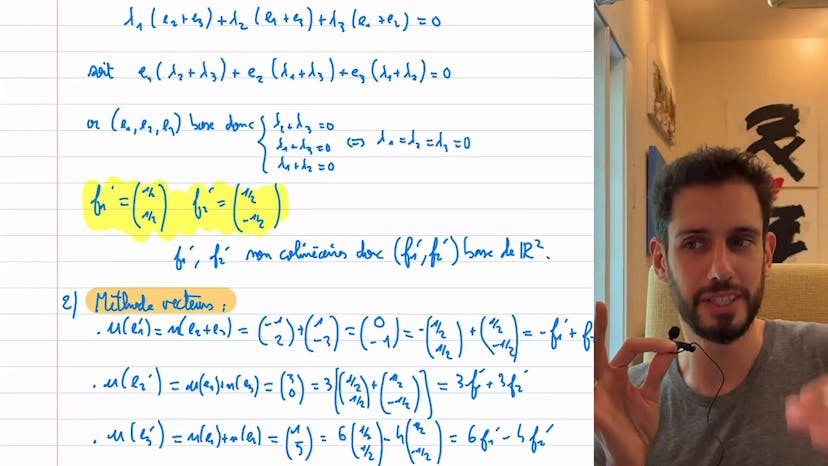
Changement de base
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Algèbre
ECG

Matrices triangulaires
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 2
Algèbre
ECG
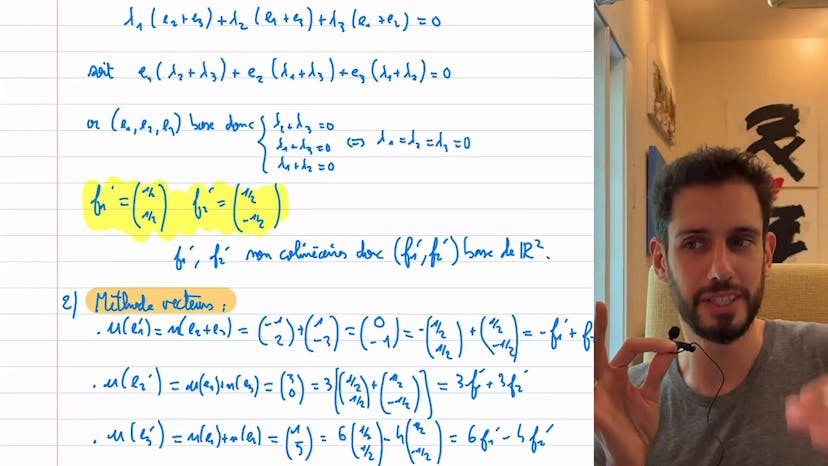
Changement de base
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 2
Algèbre
ECG

Matrices semblables
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 2
Algèbre
ECG

Matrice de passage
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 2
Algèbre
ECG
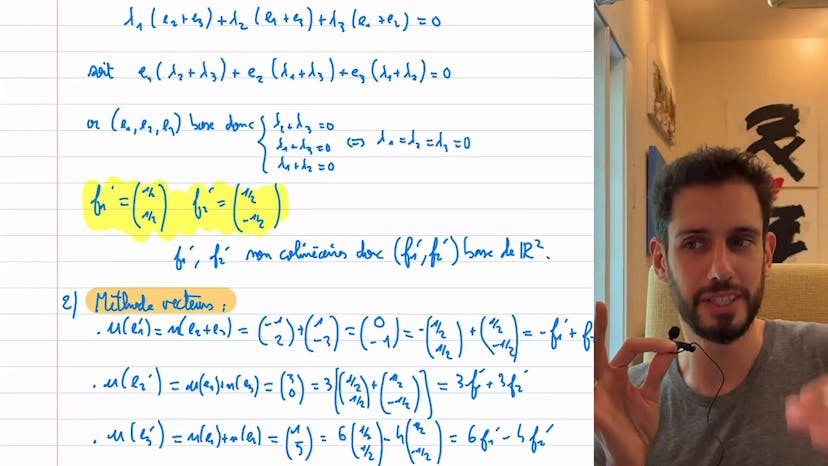
Changement de base
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 2
Algèbre
ECG

Matrices triangulaires
Aucun résumé n'est disponible pour cette vidéo


