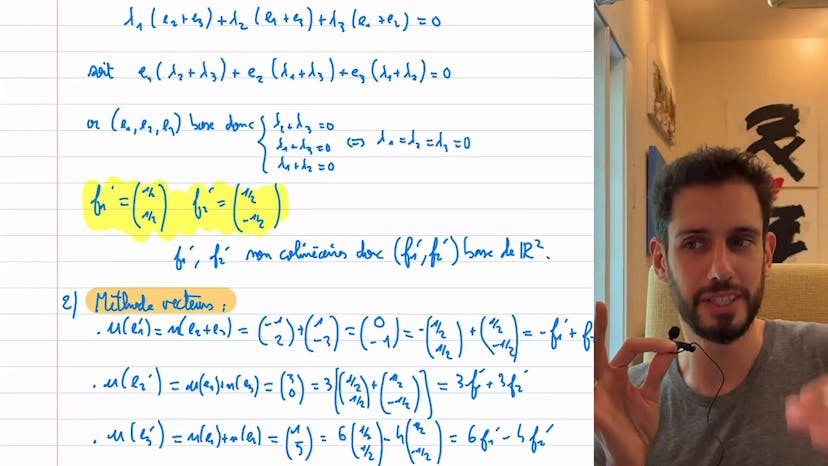Home

MPSI/PCSI

Maths

Algèbre

Changement de base, matrices de passages 

Le cours traite de l'endormorphisme U défini à partir d'une base canonique et de trois vecteurs w1, w2, w3. La matrice de cet endomorphisme est calculée en fonction de ces vecteurs. Ensuite, le cours aborde la détermination d'une base du noyau et de l'image de U, ainsi que la détermination du noyau et de l'image de l'endomorphisme U - Id, où Id est l'identité. Il est démontré que U - Id est bijective, ce qui le qualifie d'automorphisme. Enfin, le cours conclut que le noyau de cet automorphisme est réduit à zéro, ce qui signifie qu'il est inversible.

Un exercice assez classique, on vous donne une base canonique, puis trois vecteurs w1, w2, w3, et on vous dit U endomorphisme défini de la manière sûre. Bon, je ne vais pas trop me prendre la tête, on me donne les trois vecteurs, c'est-à-dire comment U traite les vecteurs de la base canonique, ça, ça me donne la matrice. J'écris la matrice 1-2, 0, 1-1, 2, 0, 0, 0, 2. Premier truc. Bon, après on vous dit exprimer w1, w2, w3, je le fais en fait en déduisant la matrice, je vous écris la matrice, vous avez compris que w1 c'était ça, w2, w3 c'est ça. Donc en gros on fait d'une pierre deux coups, w1, w2, w3, c'est à chaque fois 1 fois y1, moins 2 fois y2, plus 0 fois y3, etc. Donc j'ai la matrice, je l'appelle A, c'est top, donc soit w, x, y, z, donc juste un vecteur quelconque de taille 3, calculer U de w, je passe par le calcul matriciel, c'est plus facile. Donc je dis que U de w c'est égal, c'est un vecteur, qui est égal au vecteur A fois x, y, z, qui est égal à ça. Juste un calcul vectoriel, c'est pas très compliqué. Trouver une base de karyu, une base de imu. On fait comme d'hab, on observe. imu, moi je commence toujours par imu, imu c'est vect de ces trois là, par défaut, mais je vois très vite qu'en fait les deux premiers vecteurs sont complètement dépendants l'un de l'autre. Ils sont, comment dire, multipliés par moins 1. Les deux sont les mêmes à une constante près, à une multiplication par une constante près, en l'occurrence moins 1. Donc imu c'est vect de, je dégage le deuxième, je vais le faire comme ça, je dégage le deuxième, je trouve ça. Donc imu est de taille 2, donc le noyau est de taille 1 par le théorème du rang. Or, je viens de trouver une combinaison linéaire intéressante, là avec ça, ça vu que ça en gros c'est f de E1 et ça c'est moins f de E2, ou u pardon, moi j'ai bien, avec ça, u de E1 plus E2 égal u de E1 plus E2 égal 0, j'ai trouvé, grâce à cette combinaison linéaire que j'ai vu ici, j'ai trouvé un élément du noyau. Donc j'ai vect de 1 1 0 qui est dans le noyau, avec le théorème du rang, le noyau fait une taille 1, simple. Un ensemble de taille 1 compris dedans, lui-même est de taille 1, les deux sont égaux. J'ai donc images et noyaux qui sont déterminés, on a déjà vu ça pas mal de fois. Montrer que R3 égale ça, pour montrer que deux ensembles sont supplémentaires, une manière très très simple, une manière avec une condition nécessaire et suffisante, c'est de dire, si les bases de chacun de ces deux là, quand je les concatène, forment une base de R3, alors ils sont supplémentaires. Donc si j'ai une base de karyu, une base de imu, et que ces deux bases ensembles forment une base de l'ensemble R3, j'ai juste que les deux bases qui font la base générale, il n'y a donc pas d'élément commun, ça sera donc par définition, par caractérisation plutôt, une somme directe. Donc tout ce que j'ai à faire c'est un genre de test de liberté sur les trois éléments, ici, plus celui-là. Je fais un test de liberté, en deux secondes je trouve que ça fonctionne, et donc j'ai bien, avec les deux bases concaténées qui forment une base de R3, la somme directe. C'est pas toujours le cas, des fois il y a des éléments de imu qui sont en karyu, et vous n'avez pas la somme directe. Déterminer noyau et image de u-id, u-id c'est pas très compliqué. On va faire quoi ? On va tout de suite, tout de suite pour rendre simple et clair les choses, sinon on ne comprend rien et c'est compliqué, utiliser les matrices. C'est là qu'on voit la force des matrices, ça rend clair les choses. Donc tout de suite on écrit la matrice de u-id, et on voit si on peut facilement, de la manière qu'on vient de faire avant, trouver le noyau, trouver l'image. En déduire que c'est un automorphisme, ça veut sûrement dire que les trois colonnes vont être indépendantes, ça on prévoit à l'avance. J'écris mat de u-id, ok c'est ça, im de u-id. Pourquoi mat de u-id c'est ça ? Parce que c'est la matrice de u à laquelle j'ai retiré identité, à laquelle j'ai retiré i3 si vous voulez. Donc moi la matrice de u j'avais 1, 2, 2 ici, j'ai enlevé moins 1 sur chacun des termes diagonaux, ça fait 0, 1, 1, c'est ce qu'on retrouve ici. Donc la matrice je l'appelle B, mon im de cette matrice c'est vect du premier vecteur, du deuxième, du troisième, le premier j'ai remplacé 0-2, 0 par 0, 1, 0, c'est plus simple. Attention, je me rends compte par petite combinaison linéaire que ça en fait c'est déjà deux éléments très classiques de la base canonique. J'ai plus qu'à faire, à remplacer celui-ci et à me dire attends attends si je fais celui-ci moins celui-là, j'obtiens, si ça c'est e2, e3 et ça c'est genre u, je remplace celui-là et je dis que ça c'est en fait u-e2. Voilà, j'obtiens donc le même vect, parce que c'est juste des combinaisons linéaires, j'obtiens donc la base canonique. J'ai la base canonique classique avec, si vous voulez, triangulaire, enfin diagonale quoi, j'ai i, j et k quoi. Donc j'ai trouvé que le vect de ça c'est égal au vect de ça qui est égal à r3. Donc la matrice est surjective, enfin donc pardon, u-i est surjective, donc elle est bijective, donc le noyau est réduit à 0. Voilà, donc u-i est donc inversible. Voilà, elle est inversible. Un endomorphisme qui est bijectif s'appelle un automorphisme. J'espère que ça vous a aidé, posez des questions s'il y a besoin, à la prochaine.

Matrice de passage

RELATED

Recommended videos

Changement de base

Matrices semblables