 All subjects
All subjects
 All subjects
All subjects
Maths
Analyse
MPSI/PCSI

Suites adjacentes
Aucun résumé n'est disponible pour cette vidéo
Maths
Analyse
MPSI/PCSI
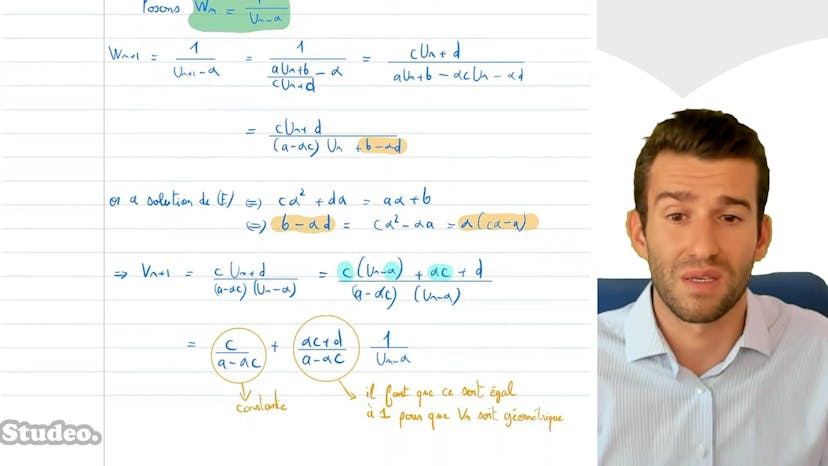
Suite homographique
Une suite homographique est une suite qui vérifie une relation de récurrence de la forme un+1=(aun+b)/(cun+d) définie par récurrence. Si la suite a deux solutions, on pose une suite auxiliaire qui est géométrique. Si elle a une seule solution, on pose une suite auxiliaire qui est arithmétique. On peut trouver l'expression de ces suites auxiliaires et remonter à l'expression de la suite homographique. On illustre cela avec deux exemples de suites homographiques.
Maths
Analyse
MPSI/PCSI

Encadrement
Dans ce cours, nous allons découvrir une astuce d'encadrement en mathématiques. Cette astuce est facile et rapide, mais il faut la maîtriser pour pouvoir l'utiliser lors d'exercices. Nous avons deux suites de règles entre 0 et 1, et nous voulons prouver que les deux convergent vers 1. Pour ce faire, nous utilisons la méthode d'encadrement en exprimant la suite un entre 1 et vn, où vn tend vers 1, et en appliquant le théorème d'encadrement pour montrer que la suite un converge vers 1. La même méthode s'applique à la suite vn. Il est important de maîtriser cette astuce car elle peut être utile dans de nombreux exercices.
Maths
Analyse
MPSI/PCSI

Suites adjacentes
Ce cours traite des suites adjacentes et leur étude de la variation. Les suites sont couplées et ont une relation de récurrence impliquant UN plus UN, UN-VN et VN plus UN. Le but est de déterminer une combinaison linéaire pour simplifier le problème. En calculant UN plus UN moins UN, on trouve que VN moins UN est une suite géométrique de raison un tiers avec un signe constant. Les sens de variation des deux suites UN et VN sont opposés, donc elles sont monotones, l'une croissante et l'autre décroissante. Les suites ont une différence qui tend vers zéro, donc elles convergent vers une même limite commune L. En trouvant la combinaison linéaire et en passant à la limite, on obtient une équation pour déterminer L. Le cours suggère de trouver soi-même les combinaisons linéaires, ce qui est un peu plus compliqué qu'en terminale.
Maths
Analyse
MPSI/PCSI

Série harmonique
Dans cet exercice sur la série harmonique, il est important de maîtriser la première étape qui montre comment la série diverge. Ensuite, nous étudions l'écart entre la série harmonique et ln(2n+1), qui converge vers une constante appelée "gamma". Pour arriver à ce résultat, nous utilisons une comparaison de série intégrale et nous encadrons l'intégrale de 1/x entre deux aires de rectangle. Pour prouver rigoureusement cette méthode, nous utilisons la stricte décroissance de la fonction 1/x. Ensuite, nous étudions les suites h(n)-ln(n) et h(n)-ln(n+1), et nous prouvons que ces suites convergent vers la même limite gamma. Nous montrons que gamma appartient à l'intervalle [1,5;1], et nous trouvons sa valeur grâce à la calculatrice ou au tableur. Enfin, nous résolvons une équation pour trouver à partir de quelle valeur de n un moins la suite vn sera inférieure à 10,2, ce qui nous permet de conclure que cette méthode est efficace. La première étape est essentielle et doit être maîtrisée sans hésitation.
Mathématiques
Analyse
ECG
Suite homographique
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Encadrement
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Suites adjacentes
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Série harmonique
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
ECG
Suites adjacentes
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Suite homographique
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Encadrement
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Suites adjacentes
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Série harmonique
Aucun résumé n'est disponible pour cette vidéo
Mathématiques
Analyse
BCPST
Suites adjacentes
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Suite homographique
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Encadrement
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Suites adjacentes
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Série harmonique
Aucun résumé n'est disponible pour cette vidéo
Maths Approfondies
Analyse
ECG

Suites adjacentes
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Suite homographique
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Encadrement
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Suites adjacentes
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Série harmonique
Aucun résumé n'est disponible pour cette vidéo
Maths Appliquées 1
Analyse
ECG

Suites adjacentes
Aucun résumé n'est disponible pour cette vidéo


