Home

MPSI/PCSI

Maths

Analyse

Suites et Convergence

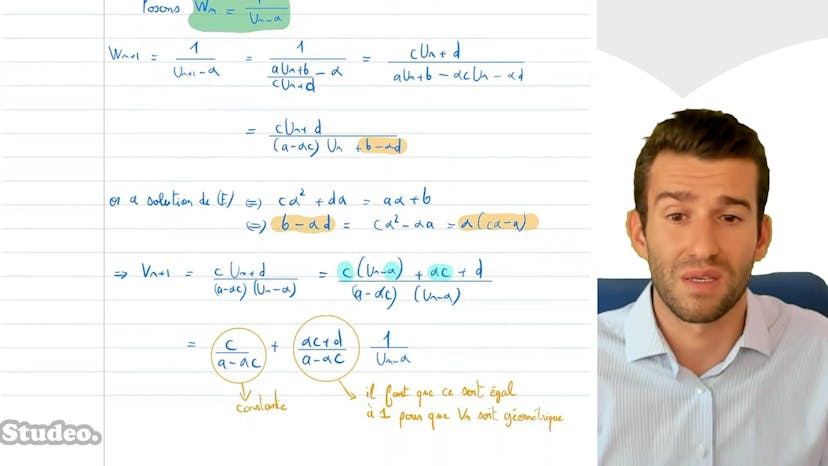
Dans cet exercice sur la série harmonique, il est important de maîtriser la première étape qui montre comment la série diverge. Ensuite, nous étudions l'écart entre la série harmonique et ln(2n+1), qui converge vers une constante appelée "gamma". Pour arriver à ce résultat, nous utilisons une comparaison de série intégrale et nous encadrons l'intégrale de 1/x entre deux aires de rectangle. Pour prouver rigoureusement cette méthode, nous utilisons la stricte décroissance de la fonction 1/x. Ensuite, nous étudions les suites h(n)-ln(n) et h(n)-ln(n+1), et nous prouvons que ces suites convergent vers la même limite gamma. Nous montrons que gamma appartient à l'intervalle [1,5;1], et nous trouvons sa valeur grâce à la calculatrice ou au tableur. Enfin, nous résolvons une équation pour trouver à partir de quelle valeur de n un moins la suite vn sera inférieure à 10,2, ce qui nous permet de conclure que cette méthode est efficace. La première étape est essentielle et doit être maîtrisée sans hésitation.

Salut à tous! Alors là on va faire un exercice qui est ultra classique, il faut absolument le maîtriser, surtout le début, c'est sur la série harmonique, donc vraiment il faut que les premières fessions vous soyez capables de refaire cet exercice sans hésiter parce que c'est vraiment quelque chose qui peut tomber en col ou à l'écrit, enfin bref c'est vraiment, c'est pas du court mais c'est presque comme si. Donc on va regarder ça mais gardez le bien en mémoire cet exercice, c'est vraiment un énorme classique. Donc comme je l'ai dit, exercice hyper classique à savoir faire, absolument évidemment. Alors comment il se décompose cet exo? Première étape, voilà donc c'est vraiment ça que pour moi il faut savoir faire sans hésiter. Et ensuite, pour montrer que la série harmonique diverge, ensuite on va regarder finalement à quelle vitesse, enfin à quel point elle s'écarte de, on va faire, on va s'intéresser à Hn-ln2n1 et on va voir que cette suite là converge vers un réel gamma, qui est la constante de l'air. Et voilà, donc cette deuxième partie est un peu moins classique, en tout cas la première faut vraiment savoir faire absolument, et deuxième c'est question bonus. Alors déjà, j'aime bien insister sur cet aspect géométrique en fait, pour trouver la réponse à la question, c'est vraiment une comparaison de série intégrale et on comprend très bien ce qui se passe en termes d'air. En fait je vais encadrer l'intégrale de la fonction 1 sur x, ici c'est 1 sur x, entre la somme en jaune, l'air en jaune, et l'air en vert. Donc l'air en vert, attention, englobe aussi, elle comprend tout ça. Et finalement c'est juste ça, la comparaison de série intégrale, c'est mettre l'air de la courbe entre deux aires de rectangle. Donc si on fait un zoom d'ailleurs sur le... entre deux entiers quelconques, k et k plus 1, ici j'ai 1 sur k, ici j'ai 1 sur k plus a, donc l'air en jaune c'est un rectangle, donc c'est 1 fois 1 sur k plus 1, l'air en vert, l'air au total c'est 1 sur k, et l'air sous la courbe, ici, c'est l'intégrale de 1 sur t entre k et k plus 1. Maintenant on va le prouver rigoureusement, parce que c'est pas un dessin, ça prouve rien, mais on a compris ce qui se passe. Donc en fait je dis que j'utilise la stricte décroissance de la fonction 1 sur x, et je dis que pour tout t appartenant à k sur k plus 1, finalement 1 sur t il est compris entre 1 sur k plus a et 1 sur k. Ensuite j'ai juste à intégrer ces relations, finalement sur l'intervalle k, k plus 1, et donc là on retrouve ce qu'on a dit géométriquement, c'est que l'air la plus petite c'est 1 sur k plus 1, l'air la plus grande des rectangles c'est 1 sur k, et ici en fait je me retrouve avec ln de k plus 1 moins ln de k quand j'intègre 1 sur t. Et quand on somme ces inégalités, en fait ici on se retrouve avec une somme télescopique, donc effectivement ça va tout se simplifier. Alors il y a un truc qui est très important aussi, c'est que pour bien trouver ces inégalités, on va pas pouvoir travailler sur les deux en même temps. On va d'abord travailler sur celle de gauche, et ensuite sur celle de droite, puisque vous allez voir qu'on les somme pas exactement sur les mêmes termes, et si on essaie de tout faire en même temps on va pas y arriver. Parce que ce qu'on veut c'est pas encadrer ça, mais c'est ça qu'on veut encadrer, donc c'est la somme d'1 sur k. Donc pour l'inégalité de gauche, je vais sommer en fait, alors là c'est un tas de tonneaux que je trouve, je peux pas commencer, attention, pour k égal 0, ça ne marche pas à cause du ln de k. C'est pas grave, je commence à k égal 1, donc mon premier terme c'est 1 demi, il manque un 1, mais c'est pas grave, je vais le faire apparaître, donc ça je reconnais que c'est hn moins 1. Vous remarquerez que je m'arrête ici à n moins 1, donc pour faire apparaître hn en fait. Si je vais jusqu'à n, ça va me faire apparaître hn plus 1, ça m'intéresse pas. Le maçon se télescope, il me reste ln de n moins ln de 1, ce qui est égal à ln de n. Donc j'ai une première inégalité, qui est que hn est plus petit que ln de n plus 1. Maintenant on s'intéresse à l'autre inégalité, là cette fois il n'y a pas de 1 sur k plus 1, ça va être plus simple, j'ai directement hn, donc là je le somme de 1 à n, pour k égal de 1 à n, ça me fait ln de n plus 1 moins ln de 1, et donc je me retrouve avec la deuxième inégalité. Donc ça c'est parfait, j'ai bien l'inégalité voulue, la double inégalité voulue, ln de n plus 1 est plus petite que hn, qui est de même plus petit que ln de n plus 1. En fait en réalité j'ai besoin que de ça, ça me permet par comparaison, comme ln de n tend vers l'infini, j'ai bien hn qui tend vers plus l'infini. Donc voilà, ça jusque là, à savoir faire parfaitement, il n'y a aucune excuse. Ensuite, deuxième partie, on va poser un égale h de n moins ln de n, et vn égale hn moins ln de n plus 1, et en fait ce qu'on va faire c'est étudier ces suites. Pour l'étude de suite on va faire le sens de variation, je fais bêtement le calcul, je calcule un plus 1 moins un, je remplace, ça fait hn plus 1 moins hn moins ln de n plus 1 plus ln. Je remarque que ce truc là je l'ai déjà lu, donc ça en fait c'est là où je dois penser, ah, je vais le mettre comme intégral, hn plus 1 moins hn ça simplifie, il ne reste plus qu'un terme, et ça il faut à tout prix penser à l'intégral, parce qu'on vient de le voir en fait. Donc finalement je peux dire que c'est 1 sur n plus 1 moins l'intégral de n à n plus 1 de 1 sur x. Et je vais rentrer ce 1 sur n plus 1 dans l'intégral, je peux parce que c'est un intervalle de longueur 1, et donc égal à l'intégral de n à n plus 1 de 1 sur n plus 1 moins 1 sur x. Comme x appartient à n à n plus 1, ce terme là il est inférieur à 0 par décroissance de la fonction 1 sur x, et donc finalement je me retrouve avec une fonction à l'intégral qui est tout le temps négative ou nulle, donc par positivité de l'intégral, l'intégral elle-même est négative ou nulle. Donc finalement un est décroissante. Ensuite, pareil pour vn, on fait la même chose, donc là c'est exactement pareil, je fais hn plus 1 moins hn, je reconnais aussi les ln sous forme d'intégral, je rentre le 1 sur n plus 1 dans l'intégral, et là c'est exactement le contraire, je vais avoir 1 sur n plus 1 moins 1 sur x, qui cette fois est positif ou nul, donc par positivité de l'intégral, c'est positif ou nul. Donc vn est décroissante. Alors, pour bien conclure, je vais utiliser évidemment que ln est plus petit que ln plus 1, donc un qui est égal à hn moins ln de n, c'est positif, vn qui est égal à hn moins ln de n plus 1, c'est positif. La question qu'on peut se poser c'est si elles doivent converger, c'est de suite vers une même limite, elles vont être adjacentes, il y en a une qui est croissante, l'autre qui est décroissante, donc en fait ce que je vais directement étudier c'est étudier la différence, je sais que la différence, j'espère, elle va tendre vers 0. Quand je fais la différence de cette suite, ça fait ln de plus 1 moins ln de n, je mets tout sous un seul ln, ça fait ln de n plus 1 sur n, ce terme là étant vers 1, donc ça tend bien vers 0. Donc finalement j'ai toutes les hypothèses qu'il faut, un est décroissante, vn est croissante, la différence tend vers 0, j'ai un et vn qui sont adjacentes et qui convergent donc vers une même limite qu'on va appeler gamma, qui est la constante de l'air. Ensuite on veut montrer que gamma appartient à 1,5,1. En fait tout simplement on calcule u1, on sait que un est décroissante, donc ça veut dire que la limite sera plus petite, donc on a gamma qui est inférieur à 1, et ensuite on calcule v1, alors v1 ça vaut 1 moins ln de 2, c'est plus petit qu'1,5, ça ne me va pas, v2 ça fait 3,5 moins ln de 3, c'est toujours plus petit qu'1,5, ça ne me va pas, et ensuite pour v3 par contre ça marche, on obtient par calcul la valeur approchée, ça fait 0,54, c'est supérieur à 1,5, la limite comme vn est croissante va être supérieure à cette valeur, et donc j'ai bien gamma qui va être supérieur à 1,5. Donc finalement gamma il est compris entre 1,5 et 1. Avec la calculette ou par tableur on trouve que gamma il va être à peu près 0,57, donc on veut savoir à partir de quelle valeur de n un moins vn est inférieur à 10,2, donc là on résout, c'est pas par la calculatrice, on résout, ça fait ln de 1 plus n sur n plus 10 que 10,2, je passe à l'exponentiel, je trouve que n est supérieur à 99,5, donc à partir de n égale 100, ça marche. Voilà pour cette méthode, je répète une dernière fois parce que c'est très important, il faut à tout prix savoir faire la première question sans aucune hésitation. Voilà pour cette méthode.

Série harmonique

RELATED

Recommended videos

Suites adjacentes

Suite homographique

Encadrement