Online Induction course by Top Instructors - Induction

Circuits couplés

Aucun résumé n'est disponible pour cette vidéo

Dans cette vidéo, Matisse de Studio explique le concept d'autoinductance et d'inductance propre d'une bobine longue. Il commence par modéliser la bobine par un solénoïde, dans lequel les effets de bord sont négligés. Le champ magnétique à l'intérieur de la bobine est défini comme étant égal à μ0N/LI, où μ0 est la permittivité du vide, N est le nombre de spires et L est la longueur du solénoïde. Ensuite, il détermine le flux propre de la bobine en utilisant l'intégrale du champ magnétique sur toute la surface de la bobine, ce qui donne μ0N²S/LI. À partir de là, il définit l'auto-inductance L comme étant le flux propre divisé par le courant, soit μ0N²S/L. En appliquant la loi de Faraday, il obtient l'équation différentielle du courant de la bobine en fonction de la force électromotrice E0, soit dI/dt + (R/L)I = E0/L. Il explique ensuite l'effet de l'auto-inductance sur la variation du courant et conclut en analysant le bilan de puissance du circuit, où la puissance délivrée par le générateur peut être dissipée par effet Joule ou stockée sous forme d'énergie magnétique dans la bobine.

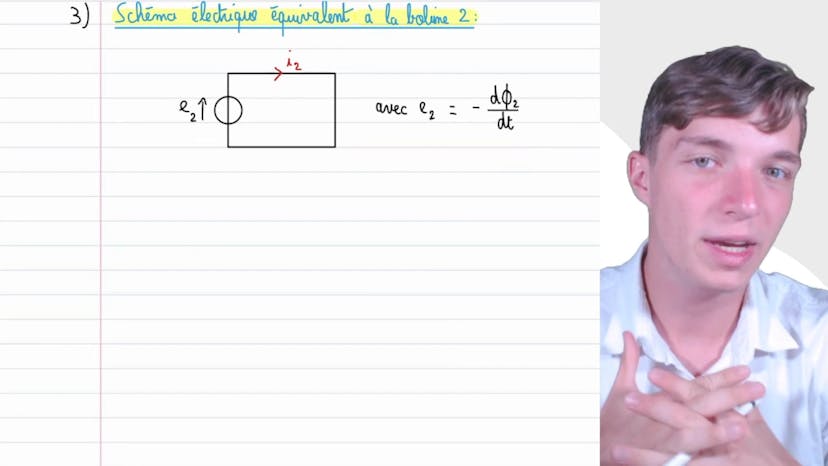
Solénoïdes emboîtés

Dans cette vidéo, nous étudions des solénoïdes emboîtés, S1 et S2, d'axes OZ, de longueur L, de nombre de spires N, et de rayons R1 et R2. Nous supposons que la longueur L est bien plus grande que les rayons, ce qui fait que nous parlons de bobine longue. La bobine 2 est en court circuit, tandis que la bobine 1 est parcourue par un courant d'intensité I1(t) = I * cos(ωt), avec I = 1A. Dans la première partie du cours, nous devons déterminer les coefficients d'induction propre L1 et L2. Pour cela, nous devons calculer le flux propre généré par chaque bobine. Ensuite, nous utilisons ces flux pour trouver les valeurs de L1 et L2. Nous trouvons que L1 = μ0 * N² * S1 / L et L2 = μ0 * N² * S2 / L. Ensuite, nous devons déterminer le coefficient d'induction mutuelle M. Pour ce faire, nous pouvons calculer le flux généré par le champ magnétique du circuit 1 vers le circuit 2 ou vice versa. Nous trouvons que M = μ0 * N² * S2 / L. Finalement, nous devons exprimer le courant I2 circulant dans la bobine 2. En utilisant les schémas équivalents et les lois de comportement, nous trouvons que I2 = (M / L2) * I1. En conclusion, nous avons calculé les coefficients d'induction propre et mutuelle ainsi que le courant circulant dans la bobine 2 pour des solénoïdes emboîtés. Ce cours nécessite une certaine attention aux calculs des flux et aux coefficients d'inductance, mais il sert de base pour des exercices plus complexes.

Mesure de M

Dans cette vidéo, Matisse de Studio explique un montage permettant de mesurer le coefficient d'inductance mutuelle entre deux bobines. Le premier circuit est classique avec une force électromotrice, une résistance et une bobine L1, tandis que le deuxième circuit est simplement une bobine L2. L'objectif est de déterminer l'intensité parcourant la bobine 2 et la tension U2 en fonction de la tension U1 et du coefficient d'inductance mutuelle M. D'abord, il est souligné que la bobine 2 est en court-circuit, donc aucune force électromotrice ou condensateur ne peut délivrer un courant dans ce circuit, ce qui signifie que l'intensité I2 est égale à 0. Ensuite, il est expliqué que la tension U2 dans le cadre de la loi classique de comportement de la bobine est égale à 0, car la tension aux bornes de la bobine 2 serait toujours nulle. Cependant, étant donné que le circuit 2 est plongé dans le champ magnétique créé par le circuit 1, les bobines sont affectées, ce qui perturbe les courants et les tensions résultants. Il est donc nécessaire de prendre en compte le circuit 1 dans l'expression de la tension U2 en utilisant le concept d'inductance mutuelle. La troisième question aborde donc l'expression de U2 en fonction de M et U1. L'inductance mutuelle est définie comme le flux du champ magnétique créé par le circuit 1 sur le circuit 2. On introduit également la notion d'auto-inductance, qui est le flux généré par le circuit 1 sur lui-même. Finalement, on obtient l'expression de U2 en fonction de I1, nécessitant de déterminer la relation entre I1 et U1 en utilisant la loi d'Ohm. Il est alors expliqué que lorsqu'il y a une dérivée dans la relation entre U1 et U2, comme c'est le cas ici, il est utile de passer par les nombres complexes pour simplifier les calculs. En utilisant les grandeurs complexes correspondant au régime sinusoidal forcé, on trouve que le coefficient d'inductance mutuelle M est égal à rU2/(2πfU1). En appliquant les valeurs numériques données dans l'exercice, U1 = 3V et U2 = 0.5V, on peut calculer M, qui est égal à 1.3 milli Henry. Ensuite, l'exercice demande de déterminer sans calcul la modification de M lorsque la bobine est tournée à 180 degrés et à 90 degrés. Lorsque la bobine est tournée à 180 degrés, seule l'inversion des branchements de l'oscilloscope se produit, donc M reste sensiblement le même. En revanche, lorsque la bobine est tournée à 90 degrés, très peu de lignes de champ magnétique du circuit 1 traversent la bobine 2, ce qui donne un coefficient d'inductance mutuelle d'environ 0. En conclusion, cet exercice détaillé permet de comprendre comment mesurer le coefficient d'inductance mutuelle entre deux circuits grâce à un montage particulier.

Négliger l'auto-induction ?

Dans cette vidéo, on se demande si on peut négliger le phénomène d'autoinduction dans un circuit, en particulier dans les circuits sans bobine. On étudie un circuit avec une bobine d'autoinductance L, une résistance R, et un champ magnétique extérieur B. On utilise des notations complexes pour résoudre les équations différentielles, et on exprime le module de H, qui représente le rapport des tensions complexes d'autoinductance par rapport au champ extérieur. On obtient une condition sur la pulsation pour négliger la force électromotrice auto-induite. En utilisant des valeurs typiques pour R et L, on calcule numériquement la pulsation, qui doit être très inférieure à 1x10^4 rad/s. On conclut en remarquant que pour un circuit avec une seule spire, on peut négliger l'autoinduction, car on se trouve à une fréquence très inférieure à 3x10^8 Hz.

Régime sinusoïdal forcé

Dans cette vidéo, on étudie une bobine dans le cadre du régime sinusoïdal forcé. On cherche à montrer que l'inductance L de la bobine est égale à mu0 N² divisé par A fois S. Pour cela, on calcule le flux propre du champ magnétique généré par la bobine, qui est égal à Mu0 N² S divisé par A. Ensuite, on ajoute un champ magnétique extérieur Bext qui est égal à B0 sinus oméga T fois EZ. On détermine la force électromotrice d'induction en prenant en compte à la fois le flux propre et le flux du champ magnétique extérieur. On obtient une équation différentielle vérifiée par le courant I, qui est d2I sur dt plus I divisé par tau est égal à moins EM sur L cosinus oméga T. On détermine l'expression de EM et de tau à partir de cette équation. Les solutions de cette équation sont cherchées sous la forme d'un courant I de T égal à IM cosinus oméga T plus Psi. On utilise la notation complexe pour déterminer l'amplitude complexe IM en fonction de EM, oméga, L et tau. On obtient IM complexe égal à moins EM tau divisé par L facteur de 1 plus J oméga tau. On détermine ensuite l'amplitude IM réelle et la phase Psi en utilisant les propriétés de l'argument d'un nombre complexe. Enfin, on analyse les valeurs obtenues sans l'auto-induction et on constate que son apport est négligeable par rapport au champ magnétique extérieur. Cet exercice complexe demande de bonnes compétences en manipulation et conceptualisation de la bobine.