Online Ondes et signaux course by Top Instructors - Ondes et signaux

Longueur d'onde

Aucun résumé n'est disponible pour cette vidéo

Cette vidéo explique comment déterminer les angles de diffraction d'une onde sonore lorsqu'elle rencontre une ouverture de largeur donnée. Pour cela, il faut utiliser la relation classique θ en radian, qui est égal à λ en mètres divisé par A en mètres. En utilisant cette relation, on peut trouver l'angle de diffraction en radian, qui peut être converti en degré en utilisant une simple règle de 3 : θ en degré = θ en radian x 180 / π. En se souvenant que les degrés sont une unité plus forte que les radians, on peut facilement se rappeler comment convertir les unités dans les deux sens.

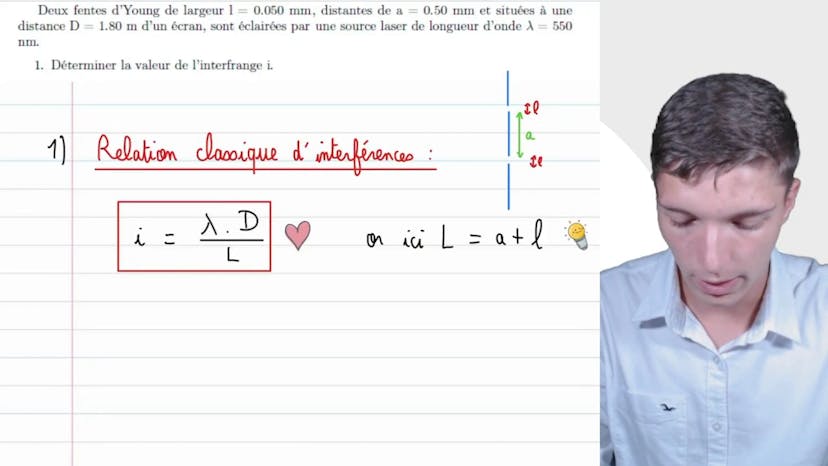
Interfrange

Dans cette vidéo, Matisse de Studio explique comment déterminer la valeur d'une interfrange en utilisant la formule classique des interférences. Il prend l'exemple de deux Fandug de largeur L, éclairées par une source laser de longueur d'onde lambda de 550 nm, à une distance de 1,80 m d'un écran. Il faut alors faire attention car A, la distance entre les franges, inclut la largeur L des fentes. La formule pour l'interfrange I est I = lambda * d / (A+L), où d est la distance entre les fentes et l'écran, et L est la distance entre les deux centres des fentes. Il est important de retenir cette relation pour tous les exercices en interférence. L'application numérique donne une valeur de 1,8 mm pour I.

Conditions nécessaire

Aucun résumé n'est disponible pour cette vidéo

Différence de marche

Dans cette vidéo, Matisse de Studio explique l'importance de la différence de marche en interférence. Il donne un exemple concret de deux vibreurs synchrones produisant des ondes à la surface d'un liquide et demande de déterminer la longueur d'onde des ondes produites pour chacun des vibreurs. Il explique ensuite comment exprimer la différence de marche entre les deux ondes en fonction de la distance B du vibreur V1 et précise la relation entre la différence de chemin et la longueur d'onde pour des interférences qui sont constructives.Matisse de Studio énumère ensuite les valeurs de B pour lesquelles l'amplitude des ondes au point P est maximale et calcule le nombre de franges d'interférences d'amplitude maximale entre les deux vibreurs. Au final, il y a 17 franges d'interférence constructive entre les deux vibreurs.Cet exercice permet de travailler les relations classiques et les manières de raisonner typiques du chapitre sur les interférences.

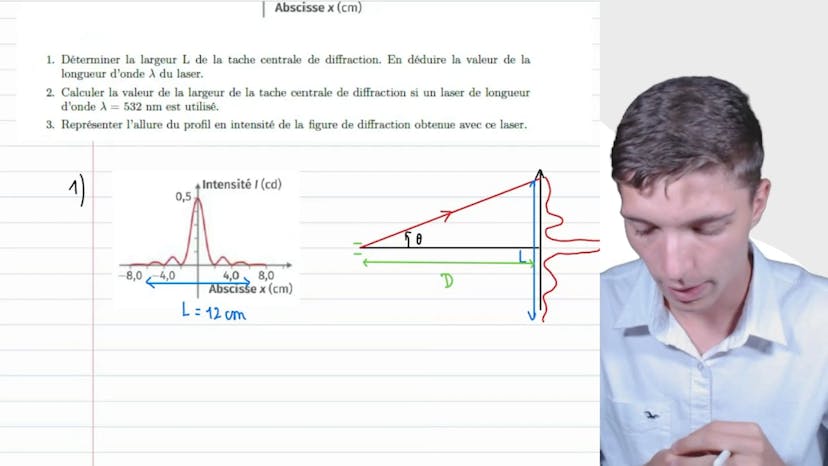
Diffraction

Dans cette vidéo, on explore le phénomène de diffraction en utilisant un laser rouge et une fente verticale de 35 micromètres. En analysant le profil en intensité de la figure de diffraction, on détermine la largeur de la tâche centrale de diffraction pour en déduire la longueur d'onde lambda du laser. On utilise une relation géométrique pour relier la tâche centrale de diffraction à l'angle de diffraction θ, qui est à son tour relié à la relation classique sin θ = λ/a. Ensuite, on utilise une application numérique pour obtenir la valeur de lambda qui est égal à 1,9 µm. Enfin, on calcule la valeur de la tâche centrale de diffraction pour un laser de longueur d'onde différente et on obtient une tâche beaucoup plus petite avec un profil de densité plus serré. L'exercice permet de comprendre l'importance d'identifier la relation géométrique et la relation classique pour obtenir les valeurs des grandeurs qui nous intéressent.

Enceintes

Dans cette vidéo, on apprend que les enceintes sont constituées d'un caisson avec un haut-parleur et une ouverture de diamètre d. On calcule la longueur d'onde des ondes sonores de fréquences 200 Hz, 2 Hz et 20 kHz en utilisant la relation classique ondulatoire. On déduit que les sons avec la longueur d'onde la plus grande seront les mieux diffractés. Une personne placée sur le côté de l'enceinte percevra mieux les sons graves car la longueur d'onde est inversement proportionnelle à la fréquence. Les enceintes comportent au minimum deux haut-parleurs, le woofer et le tweeter, avec des diamètres différents car le tweeter transmet principalement les sons aigus et a un plus petit diamètre pour compenser le phénomène dissipatif d'écartement vis-à-vis de la longueur d'onde.

Digue et vagues

Cette vidéo traite de l'impact de la diffraction sur les vagues atteignant une digue de port de plaisance et de l'effet de cette diffraction sur deux bateaux se trouvant à proximité. Des vagues de 1 mètre de hauteur sont espacées de 30 mètres et peuvent traverser une passe de 40 mètres. En utilisant les paramètres clés des ondes, l'amplitude d'une vague est de 0,5 mètre, la longueur d'onde est de 30 mètres et la largeur de la fente est de 40 mètres. En appliquant la relation classique pour le calcul de l'angle d'ouverture de diffraction, on obtient θ égal à 0,75 radian, soit 43 degrés. Le bateau 2 est mieux protégé de la houle par la digue que le bateau 1.

Révisions Physique Lycée