Online Ondes et signaux course by Top Instructors - Ondes et signaux

Ambulance

Dans cette vidéo éducative sur l'ambulance, nous sommes présentés à un exercice classique qui implique le calcul du décalage de fréquence. L'ambulance passe et émet un son à une fréquence de 435 Hz alors qu'elle s'éloigne d'un piéton immobile à une vitesse de 80 km/h. Pour trouver le décalage d'opéraire, nous pouvons utiliser la formule delta f, qui est moins fe fois v sur v son plus v. Nous rappelons que la célérité du son est de 345 m/s et la conversion de km/h en m/s est nécessaire. Nous trouvons que le delta f est moins 26 Hz, ce qui signifie que le piéton entend une fréquence de 409 Hz. Cette fréquence est plus grave que celle émise par l'ambulance, ce qui est cohérent avec notre observation de la baisse de fréquence lorsqu'un véhicule s'éloigne de nous.

Le radar

Dans cette vidéo, Layla explique le principe de fonctionnement d'un radar. L'onde FE émise par le radar et réfléchie sur le véhicule revient avec une fréquence différente due à l'effet Doppler. La formule pour calculer la vitesse du véhicule est V= delta F x C / 2FE cos alpha. La conversion de la vitesse en mètre par seconde en kilomètre heure est de 1 m/s = 3.6 km/h. Layla a trouvé une vitesse de 147 km/h pour le véhicule mesuré par le radar.

Alarme incendie

Dans ce cours, Laëla de Studio donne un exercice sur une alarme incendie en utilisant l'intensité sonore en watts par mètre carré à une distance d'un mètre. Elle rappelle la surface d'une demi-sphère et explique comment passer de l'intensité sonore à la puissance sonore. Après avoir isolé la formule, elle applique les données du rayon de la sphère pour trouver la puissance sonore. La vidéo souligne l'importance de toujours utiliser les unités appropriées et de faire attention aux chiffres significatifs. Poser des questions en commentaire est encouragé.

Sonar

Le cours explique comment fonctionne un sonar pour mesurer la vitesse d'un sous-marin dans l'eau en utilisant la formule de l'effet Doppler. Le décalage en fréquence est calculé en utilisant la fréquence émise et la fréquence reçue, puis la vitesse du sous-marin est trouvée en utilisant cette formule. Enfin, la vitesse est convertie en km/h à partir de m/s. La vidéo est instructive et les questions sont les bienvenues.

Eloignement d'une galaxie

Dans cette vidéo, on apprend comment utiliser l'effet Doppler pour déterminer la vitesse d'éloignement d'une galaxie en astrophysique. Pour cela, on mesure le décalage de la longueur d'onde de l'hydrogène observé sur Terre par rapport à celui observé dans la galaxie. On utilise ensuite la formule V = delta lambda C / lambda E pour isoler la vitesse d'éloignement, qui est de 1,2 x 10^7 m/s dans ce cas. On peut ensuite utiliser la constante de Hubble et la distance en années-lumières pour calculer la distance entre la galaxie et la Terre, soit 5,2 x 10^8 années-lumière. La vidéo explique également que la lumière qu'on observe d'une galaxie est ce qui s'est passé il y a de nombreuses années, donnant ainsi un aperçu du passé en astrophysique.

Bruit sur un chantier

Dans cette vidéo, on évalue le bruit d'un chantier pour savoir si cela peut causer des dommages auditifs à un ouvrier. On utilise l'expression de la dilution sphérique pour déterminer la puissance sonore émise par l'engin à différentes distances. On utilise aussi une formule pour calculer le niveau d'intensité sonore en décibels. Le seuil de danger pour le système auditif est de 85 dB. On montre l'importance de porter des casques anti-bruit, qui ont une atténuation d'au moins 20 dB, afin de protéger l'ouïe. En se déplaçant à 10 mètres, ou en portant un casque anti-bruit à un mètre, l'ouvrier est protégé et le niveau d'intensité sonore est en dessous du seuil de danger.

Voiture et effet Doppler

Aujourd'hui, dans cet exercice sur l'effet Doppler, nous étudions ce qui se passe lorsque qu'une voiture s'approche d'un piéton. La voiture se déplace le long de l'axe OX à une vitesse constante V et émet un son de fréquence FE. Le piéton se situe à une distance D de l'axe. Tout d'abord, nous devons déterminer cosθ en fonction de X et D. En utilisant les formules trigonométriques, nous savons que cosθ est le côté adjacent sur l'hypoténuse. Ici, le côté adjacent est X et l'hypoténuse est √(D² + X²). Donc, nous avons cosθ = X/ √(D² + X²). Ensuite, nous pouvons utiliser cette formule pour calculer la fréquence reçue (FR) en fonction de X. La formule est FR = FE * (1 + (V * cosθ) / (V du son) * √(D² + X²). Cette transformation de cosθ en X est utile car X est le seul paramètre dont nous disposons. Ensuite, nous examinons quatre graphiques et devons déterminer lequel représente l'évolution de la fréquence en fonction de X. Pour cela, nous pouvons utiliser l'élimination. Nous savons que FR est une fonction décroissante, car plus X augmente, plus la fréquence diminue. De plus, lorsque X = 0, FR doit être égal à FE, car le piéton est directement en face de la voiture. Parmi les graphiques proposés, seul celui de la figure 1 satisfait ces critères. Ensuite, nous analysons comment la courbe évolue si V ou D augmentent. Si V augmente, FR augmente également car V est dans le numérateur de la formule. De même, si FE augmente, FR augmente aussi car FE est un facteur de la formule. En revanche, si D augmente, FR diminue car D est situé dans le dénominateur de la formule. En résumé, lorsque la voiture s'approche du piéton, la fréquence reçue diminue. La figure 1 représente l'évolution de la fréquence en fonction de la distance X. Si la vitesse de la voiture ou la distance entre la voiture et le piéton augmentent, la fréquence reçue augmente. N'hésitez pas à poser vos questions en commentaire.

Casque à réduction de bruit

Dans ce cours, Layla de CEDEO explique le concept de réduction de bruit active sur les casques audio. Lorsqu'on active la réduction de bruit sur nos casques, un signal anti-bruit est émis pour combiner avec le bruit ambiant, ce qui crée l'impression d'absence de bruit. Le cours présente plusieurs configurations de casques : sans casque, avec une réduction de bruit passive (casque isolant) et avec une réduction de bruit active. Un graphique montre comment ces différentes configurations affectent le niveau d'intensité sonore en fonction de la fréquence. Il est expliqué que le casque passif n'est efficace que pour certaines fréquences graves, tandis que la réduction de bruit active est plus efficace dans une zone spécifique (zone B). Dans une autre zone de transition, les deux types de réduction de bruit sont efficaces, mais avec des degrés d'efficacité variables en fonction de la fréquence. Dans la dernière zone, les deux types de réduction de bruit sont également efficaces. 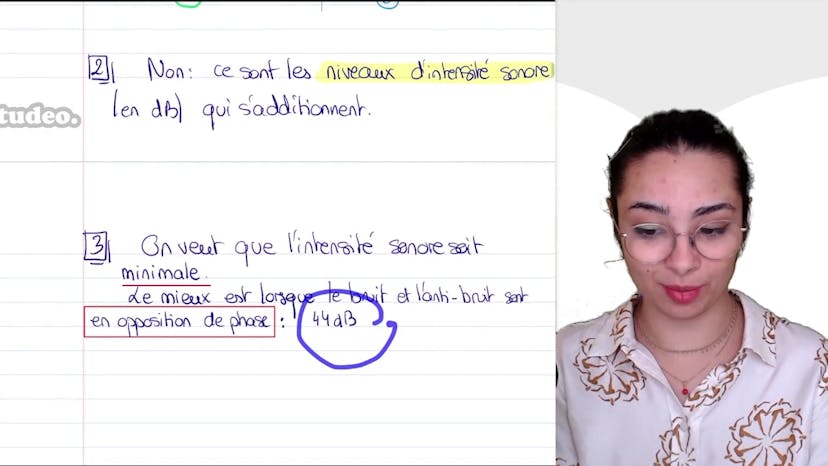Ensuite, le cours aborde la question de l'émission simultanée de bruit et d'anti-bruit dans différentes situations. On explique que ce sont les niveaux d'intensité sonore qui s'additionnent, pas les intensités sonores elles-mêmes. Les niveaux d'intensité sonore sont mesurés en décibels. Enfin, on demande quelle situation est la plus efficace pour le dispositif de réduction active de bruit. La réponse est lorsque le bruit et l'anti-bruit sont en opposition de phase, ce qui entraîne la plus grande atténuation du niveau sonore.

Vélocimétrie Doppler

La vélocimétrie Doppler est une méthode non-invasive pour mesurer la vitesse du sang, souvent utilisée en médecine pour détecter des problèmes vasculaires. On utilise une sonde émettant des ultrasons à une certaine fréquence, les globules rouges affectent ensuite cette onde avec une fréquence différente à cause de l'effet Doppler. On peut déterminer la vitesse des globules rouges en analysant un spectre et en isolant les fréquences correspondant à la fréquence émise et reçue. On applique ensuite une formule pour trouver la vitesse des ultrasons qui nous donne une vitesse d'environ 42 cm par seconde, correspondant à l'ordre de grandeur de la vitesse du sang dans le corps humain.

Musiciens dans un train

Dans cette vidéo, Christophe Buballot a mené une expérience pour vérifier l'effet Doppler en plaçant des musiciens dans un train qui jouaient une note (La 440) et en faisant écouter cette note à des auditeurs le long de la voie. Les auditeurs ont perçu une fréquence différente de la note émise en raison du mouvement de l'onde sonore par rapport à eux. La fréquence reçue dépendait de la note jouée par les musiciens, qui était exprimée en Hertz. En utilisant la formule de l'effet Doppler, la vitesse du train a été calculée à partir de l'écart entre la fréquence émise et la fréquence reçue des notes. La vitesse calculée était de 63,4 km/h, ce qui est raisonnable pour un train de l'époque.

Longueur d'onde

Aucun résumé n'est disponible pour cette vidéo