Online Mouvements et intéractions course by Top Instructors - Mouvements et intéractions

Chute d'un projectile

Le cours porte sur la chute d'un projectile et présente un exercice de type vrai ou faux. On nous donne une situation où un projectile est lancé d'un point O avec une vitesse initiale et un angle alpha par rapport à l'horizontale dans un champ de pesanteur uniforme G. La première affirmation est que le vecteur accélération A du projectile ne dépend pas des conditions initiales. En appliquant le principe fondamental de la dynamique, on trouve que l'accélération est égale à G, ce qui confirme que A ne dépend pas des conditions initiales. Ensuite, la question est de savoir si le mouvement du projectile est plan. Un mouvement est plan s'il n'est contenu que dans deux dimensions. En étudiant la vitesse du projectile, on constate que la composante selon Z est nulle, ce qui signifie que le mouvement est effectivement plan, uniquement selon les composantes X et Y. La troisième affirmation concerne la trajectoire du projectile, on nous dit qu'elle est parabolique quelle que soit la valeur de alpha. Pour vérifier cela, on peut trouver un contre-exemple où la trajectoire n'est pas parabolique. Si on lance le projectile verticalement vers le bas, la trajectoire est rectiligne, pas une parabole. Donc, cette affirmation est fausse. Enfin, la dernière affirmation est que pour un lancer horizontal, l'abscisse du point de chute est donnée par x = v0 * racine de (2h/g), où h est la hauteur initiale du projectile. En utilisant l'équation de la trajectoire, on trouve cette expression pour x et en l'injectant dans l'équation, on vérifie que y de x est bien égal à 0. Donc, cette affirmation est vraie. En résumé, le vecteur accélération A du projectile ne dépend pas des conditions initiales. Le mouvement du projectile est plan, se déroulant dans les composantes X et Y. La trajectoire du projectile n'est pas toujours parabolique, sauf dans certains cas. Pour un lancer horizontal, l'abscisse du point de chute est donnée par x = v0 * racine de (2h/g).

Solide et ressort

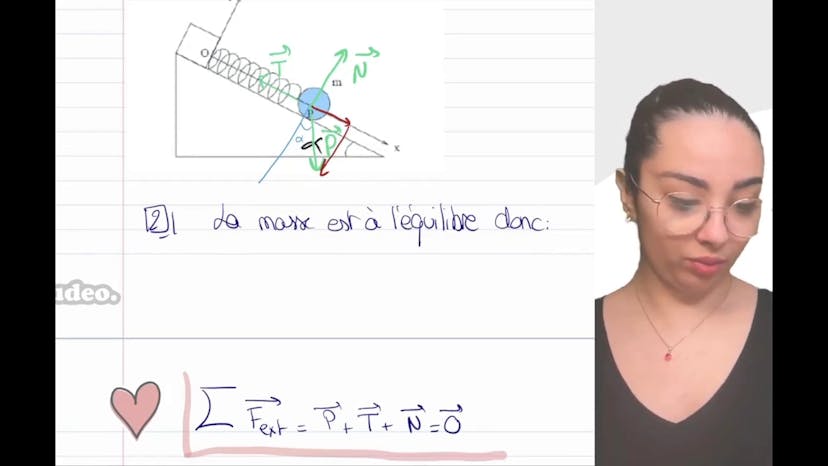
Dans ce cours, nous étudions un exercice de mécanique portant sur un solide accroché à un ressort. Le solide est à l'équilibre et se trouve sur un plan incliné. Trois forces agissent sur le solide : le poids, la tension du ressort et la réaction du support. La première question consiste à représenter ces forces. Pour cela, il faut faire un bilan des forces, qui se compose de la force de rappel du ressort (T), du poids (P) et de la réaction du support (N). Ensuite, nous devons calculer l'angle alpha. Pour cela, nous utilisons le fait que le système est à l'équilibre. En utilisant le principe fondamental de la statique, qui stipule que la somme des forces extérieures est nulle à l'équilibre, nous détaillons les forces. Nous projetons le poids selon les axes x et y. Sur l'axe y, nous obtenons -cos(alpha)*P et sur l'axe x, nous avons sin(alpha)*P. Nous utilisons ensuite ces projections dans l'équation de l'équilibre. La troisième question demande de déterminer la norme de la réaction du support. Nous observons que cette réaction apparaît dans la première équation. Nous la calculons en utilisant la relation trigonométrique fondamentale : cos^2(alpha) = 1 - sin^2(alpha). En substituant cette relation dans l'expression de la réaction normale du support, nous obtenons N = P*cos(alpha) = mg*racine(1 - (T^2)/(m^2g^2)). J'espère que cet exercice vous a été utile. N'hésitez pas à poser vos questions en commentaire.

Particule chargée

Aujourd'hui, nous allons étudier les particules chargées en mouvement dans un champ électrique uniforme, plus précisément entre les plaques d'un condensateur. La première étape consiste à représenter le champ électrique (E) et l'accélération (A). En utilisant le principe fondamental de la dynamique, on peut établir que mA (avec m étant la masse de la particule) est égal à la force électrique, c'est-à-dire Q (charge de la particule) multiplié par E. Si la particule est chargée positivement, la direction de l'accélération sera la même que celle du champ électrique. Ensuite, on nous demande de déterminer le signe des charges des plaques du condensateur. En général, le champ électrique va du positif vers le négatif, ce qui signifie que la plaque chargée positivement sera à gauche et la plaque chargée négativement sera à droite. La trajectoire de la particule peut également être déterminée si l'on sait que le vecteur V0 est perpendiculaire aux plaques. En utilisant les équations de base et le principe fondamental de la dynamique, on peut trouver que la trajectoire sera rectiligne uniquement dans la direction horizontale (X) et que la vitesse verticale (Y) sera nulle. Enfin, si la particule est chargée négativement, la force électrique sera dirigée dans la direction opposée à l'accélération. En utilisant les formules, on peut déduire que si la charge (Q) est positive, le VX (vitesse horizontale) sera toujours positif, tandis que si la charge est négative, le VX deviendra négatif après un certain temps. Le VY (vitesse verticale) reste inchangé. Si vous avez des questions, n'hésitez pas à les poser.

Champ éléctrique

Aujourd'hui, nous allons étudier le champ électrique et sa relation avec la tension entre deux plaques. Nous avons deux plaques, A et B, d'un condensateur, et un générateur de tension constant. Le champ électrique E entre les deux plaques est donné, ainsi que la distance entre les plaques. Notre objectif est de déterminer la tension UAB entre les plaques. Pour cela, nous utilisons la formule UAB sur D = U, où U est la tension en volts et D est la distance en mètres. En substituant la valeur du champ électrique E donnée en newton par coulomb (qui est équivalente à volts par mètre), nous obtenons UAB = E x D. En effectuant le calcul numérique, nous trouvons UAB = 1 x 10^3 volts, soit des kilovolts. Nous remarquons également que si la distance D augmente, la tension UAB augmente également, à champ électrique constant. En résumé, ce cours porte sur la détermination de la tension entre deux plaques d'un condensateur en utilisant la formule UAB = E x D. Nous avons appris que le champ électrique est exprimé en volts par mètre et que la distance est en mètres. En augmentant la distance, la tension augmente également.

Accélération d’une bille

Dans ce cours, nous allons travailler sur l'accélération d'une bille soumise uniquement à la pesanteur terrestre. Le repère utilisé est OIG. La première étape consiste à déterminer le vecteur d'accélération de la bille en utilisant la deuxième loi de Newton qui stipule que la somme des forces extérieures est égale à la masse multipliée par l'accélération. Comme la bille est soumise uniquement à son poids (P = mg), on peut écrire que MA = MG, ce qui nous donne A = G. Ensuite, on nous demande les coordonnées de l'accélération dans le repère cartésien OIG. Pour cela, nous devons décomposer le vecteur G sur la base OIG. On peut observer que G est selon moins G, donc les coordonnées de l'accélération sont -G fois G. En termes de vecteurs, la première ligne représente toujours le premier vecteur de la base (I) et la deuxième ligne représente toujours le deuxième vecteur (G). N'hésitez pas à poser vos questions si nécessaire.

Mouvement plan

Dans ce cours, Leïla explique comment déterminer le vecteur vitesse à partir d'un vecteur d'accélération. Elle rappelle la formule d'accélération comme la dérivée de la vitesse par rapport au temps et explique qu'il faut intégrer les coordonnées une par une en prenant en compte les constantes d'intégration. En intégrant les coordonnées selon X, Y et Z, Leïla obtient une vitesse constante selon Z et une vitesse qui varie avec le temps selon Y. Elle utilise ensuite les conditions initiales pour déterminer les constantes d'intégration. Elle utilise les expressions données pour obtenir les coordonnées du vecteur vitesse, notées VX, VY et VZ. Ensuite, elle analyse si le mouvement est plan en vérifiant s'il se déplace uniquement dans deux dimensions. Dans cet exemple, Leïla constate que la vitesse est nulle selon X, ce qui signifie que le mouvement ne progresse pas dans cette direction. Par conséquent, le mouvement se fait uniquement selon Y et Z, ce qui prouve qu'il est plan. Plus précisément, il est dans le plan OYZ. N'hésitez pas à poser vos questions ou à faire part de vos remarques.

Masse à l’équilibre

Aujourd'hui, nous allons étudier une masse suspendue à un fil et soumise à la tension du fil ainsi qu'à son poids. L'objectif est de montrer pourquoi cette masse ne peut pas être en équilibre. Si nous examinons rapidement le problème, il semble évident qu'il s'agit d'un pendule simple. Si je déplace le pendule d'un certain angle, il reviendra à sa position initiale, il ne restera pas là tout seul. Pour expliquer cela à l'aide des lois que vous avez étudiées dans le chapitre, nous pouvons utiliser la loi de Newton, qui stipule que la somme des forces exercées doit être nulle pour être en équilibre. Dans ce cas, la somme des forces est T (la tension du fil) plus P (le poids), et cette somme n'est pas nulle, ce qui signifie que le système n'est pas en équilibre. Pour illustrer cela, nous pouvons utiliser la relation de Charles pour faire la somme des forces vectorielles. Si je déplace le poids et le place à côté de la flèche représentant la tension, la somme des forces vectorielles est représentée par le vecteur vert. Comme ce vecteur n'est pas nul, cela signifie que la masse n'est pas en équilibre. En ce qui concerne l'équilibre, si la masse passe par l'axe vertical, le poids est dirigé vers le bas et la tension vers le haut, ce qui permet d'atteindre l'équilibre. C'est pourquoi si l'on prend un pendule et qu'on le déplace, avec le temps, il reviendra à une position verticale, car c'est là qu'il atteint l'équilibre avec une somme des forces nulle. N'hésitez pas à poser vos questions en commentaire.

Projections

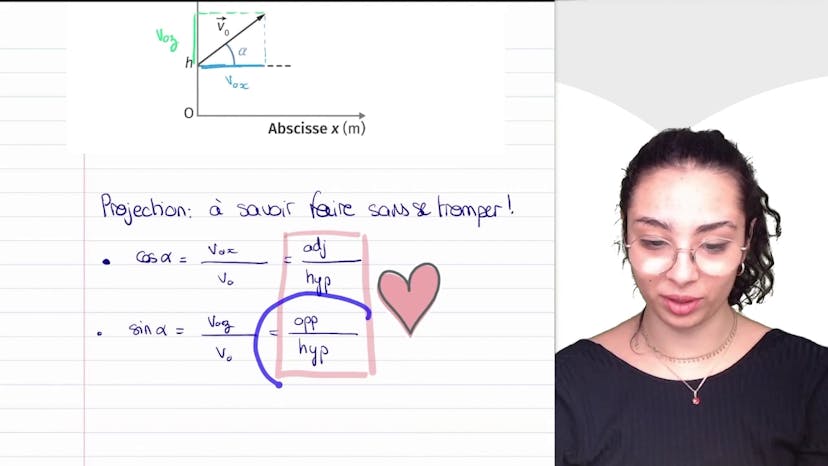
Aujourd'hui, nous allons travailler sur des projections, ce qui est important dans tous les exercices où des vecteurs sont donnés. Lorsque vous résolvez ces exercices, il est essentiel de déterminer ce qui se passe en fonction des angles. Au début, cela peut être un peu difficile car vous ne voyez pas bien où se trouvent les angles, etc. Mais nous allons le faire ensemble et vous devez garder cette technique à l'esprit. Ici, nous avons un vecteur V0 qui se décompose en composantes selon Z et X. Le but est donc de déterminer précisément les composantes selon X et Z. C'est quelque chose que vous allez trouver fréquemment dans les problèmes de mécanique. Que devons-nous faire ? Tout d'abord, nous devons regarder l'angle entre les deux. Ici, nous avons un angle avec l'horizontale appelé alpha. Dans les projections, il y a toujours des cosinus et des sinus. Avec de la pratique, vous pourrez directement identifier s'il s'agit d'un cosinus ou d'un sinus. Au début, si vous n'êtes pas sûr, je vous conseille de revenir aux formules de base. Ainsi, le cosinus d'un angle est le côté adjacent sur l'hypoténuse, tandis que le sinus d'un angle est le côté opposé sur l'hypoténuse. Il n'y a pas de tangente dans les formules de projection, car c'est toujours l'hypoténuse qui est en jeu. Je commence donc par écrire les valeurs de cos alpha et sin alpha, puis j'établis le lien avec V0x et V0y. Cos alpha est le côté adjacent sur l'hypoténuse, tandis que sin alpha est le côté opposé sur l'hypoténuse. Il ne faut pas se tromper : le côté adjacent est celui qui mène à l'angle droit, tandis que le côté opposé est de l'autre côté de l'angle droit par rapport à l'angle alpha. Une fois cela établi, j'ai une relation avec V0x, V0z, V0, cosinus et sinus. Cela me donne V0x = V0 cos alpha et V0z = V0 sin alpha. Je peux alors décomposer ces valeurs selon les vecteurs EX et EY. C'est ce qu'on appelle la projection, qui permet de déterminer les composantes selon X et Y. J'espère que cela vous a été utile, n'hésitez pas à poser vos questions.

Révisions Physique Lycée