 All subjects
All subjects
 All subjects
All subjects
Physique-Chimie
Chimie
MPSI/PCSI

Conbustion du souffre
Dans cette vidéo, nous étudions la combustion du soufre. Nous introduisons dans un creuset 0,30 g de soufre pur solide sous forme de poudre jaune. Nous enflammons le soufre avec un bec benzène et plaçons immédiatement le creuset dans un flacon d'air sous pression de 1 bar. Nous observons une combustion lente du soufre avec une flamme bleue caractéristique. La réaction chimique de combustion est donnée par l'équation : soufre solide + dioxygène gazeux -> dioxyde de soufre gazeux. L'air est un mélange constitué à 80% de diazote et 20% de dioxygène. Le diazote n'est pas réactif dans cette transformation. La température est supposée constante à 25 degrés. La constante d'équilibre de la réaction de combustion est extrêmement élevée (4x10^52), donc la réaction peut être considérée comme étant totale.
Pour étudier l'évolution de la transformation, nous devons d'abord calculer les quantités de matière initiale de soufre, de dioxygène et de diazote présentes dans le flacon. La quantité de matière initiale de soufre est de 9,3x10^3 mol. Pour le dioxygène et le diazote, nous utilisons la quantité de matière d'air dans le flacon (calculée à l'aide de la loi des gaz parfaits) pour déterminer ces quantités de matière. La quantité de matière initiale de dioxygène est de 8,1x10^3 mol et celle de diazote est de 32x10^3 mol.
En construisant le tableau d'avancement de la réaction, il est clair que le réactif limitant est le dioxygène, car la quantité de matière initiale de soufre est supérieure à celle de dioxygène. Donc l'état final de la réaction est un équilibre, bien que la réaction puisse être considérée comme totale en raison de la constante d'équilibre élevée.
La quantité totale de gaz au cours de la transformation reste constante, ce qui signifie que la pression dans le flacon reste constante également.
Enfin, la composition finale du système est donnée par la différence entre les quantités de matière initiale et finale de soufre. La masse finale de soufre est de 0,039 g. La pression partielle finale de dioxygène est de 0, tandis que la pression partielle finale de dioxyde de soufre est égale à la pression partielle initiale de dioxygène (20 kPa).
En résumé, cette vidéo a analysé la combustion du soufre, en fournissant des calculs quantitatifs des quantités de matière et de la pression tout au long de la réaction.
Physique-Chimie
Chimie
MPSI/PCSI

Pentachlorure de phosphore
Dans cette vidéo, nous traitons du pentachlorure de phosphore, un composé toxique utilisé en synthèse organique pour ajouter des atomes de chlore à une chaîne carbonée. En phase gazeuse, il se décompose en trichlorure de phosphore et en dichlore, atteignant un équilibre en phase gazeuse.
Nous examinons un réacteur fermé d'un volume constant de 2 litres, maintenu à une température constante de 180 degrés. À cette température, la constante thermodynamique de l'équilibre, notée K0, est égale à 8. Nous y introduisons 0,5 mol de PCl5. Que va-t-il se passer ?
Tout d'abord, nous devons écrire l'équation de réaction qui décrit le processus dans le réacteur. Sur la base de la stoichiométrie, nous formons du trichlorure de phosphore et du dichlore. Ainsi, nous obtenons l'équation suivante : PCl5 (gaz) = PCl3 (gaz) + Cl2 (gaz).
Ensuite, nous construisons un tableau d'avancement relatif à cette réaction, où nous commençons avec un avancement de XI. Nous avons ici un coefficient stoichiométrique de 1.
La question suivante consiste à exprimer les pressions partielles des gaz en fonction de N0, de l'avancement et de la pression initiale P0. Nous utilisons la loi des gaz parfaits pour obtenir la pression initiale P0, qui est égale à N0 RT / V, où RT / V est P0 / N0. Ainsi, nous obtenons PCl5 = (1 - XI / N0) * P0. De manière similaire, nous obtenons PCl3 = XI * P0 / N0 et Cl2 = XI * P0 / N0.
Ensuite, nous devons calculer le coefficient de dissociation à l'équilibre, noté α, qui est égal à XI / N0. Nous utilisons la constante d'équilibre K0 pour obtenir α. Nous réarrangeons l'expression pour K0 pour obtenir une équation du second degré et calculons α en utilisant les racines de cette équation. Dans ce cas, α est égal à 0,0029. Physiquement, cela représente la proportion de PCl5 qui se transforme à l'équilibre.
Enfin, nous calculons la pression totale dans le réacteur à l'équilibre. Nous utilisons la loi de Dalton pour obtenir la somme des pressions partielles, ce qui donne une pression totale de 1 + α * P0. En appliquant les valeurs numériques, nous obtenons une pression totale de 9,44 bar à l'intérieur du réacteur.
Il est important de noter que cet exercice peut être complexe en raison de la dissociation du gaz en deux composés, ce qui entraîne une augmentation de pression. Il faut également faire attention à l'expression des différentes grandeurs mentionnées.
Merci d'avoir regardé cette vidéo et à bientôt !
Physique-Chimie
Chimie
MPSI/PCSI

Décomposition thermique du gypse
Dans cette vidéo, Mathis de studio aborde la décomposition thermique du gypse. Le gypse, qui est du sulfate de calcium CaSO4 solide, réagit en présence de sable pour former du silicate de calcium CaSiO3 solide. Le ciment de Portland est obtenu en chauffant ce mélange avec du charbon et de l'argile. Deux équilibres chimiques sont mis en jeu dans ce processus. Le premier équilibre est CaSO4 + SiO2 ⇌ CaSiO3 + SO3, et le deuxième équilibre est 2SO3 ⇌ 2SO2 + O2. Les valeurs des constantes d'équilibre à une température de 1400 kelvin sont K01 = 0,950 et K02 = 400. Le cours présente ensuite une étude sur un système de volume fixe de 10 litres contenant une molécule de CaSO4 et une molécule de SiO2. À la température de 1400 kelvin, le système atteint son état final. L'objectif est de déterminer les pressions partielles des trois gaz constituant le mélange gazeux final ainsi que les quantités de matière des solides présents. L'exercice requiert une approche méthodique et une étude des équilibres chimiques impliqués. Les constantes d'équilibre sont exprimées en fonction des pressions partielles des gaz, et les quantités de matière des solides sont calculées à partir des avancements de réaction. Les résultats numériques sont ensuite donnés pour illustrer la résolution de l'exercice. En conclusion, il est souligné que cet exercice est complexe et nécessite une analyse approfondie des équilibres chimiques en présence.
Physique-Chimie
Chimie
MPSI/PCSI

Dissociation du calcaire
Dans cette vidéo, Mathis du studio explique la dissociation du calcaire et comment obtenir de la chaux vive solide (CaO) en industrie.
Il précise que la chaux vive est obtenue par dissociation thermique du calcaire (CaCO3) selon la réaction suivante : CaCO3 solide = CaO solide + CO2 gazeux. La constant d'équilibre de cette réaction à 1100 Kelvin est de 0,358.
Mathis présente ensuite une question : dans un réacteur de 10 litres contenant de l'air exempt de dioxyde de carbone à une pression de 1 bar, on introduit 10 millimoles de calcaire. Un thermostat maintient la température à 1100 Kelvin. Il faut déterminer le sens d'évolution et décrire l'état final attendu.
Il explique qu'il faut comparer le quotient de réaction initial avec la constante d'équilibre de réaction pour déterminer le sens d'évolution. Comme le quotient de réaction initial est inférieur à la constante d'équilibre, la réaction aura lieu dans le sens réactif vers produit.
Pour décrire l'état final attendu, il utilise le tableau d'avancement. En utilisant la constante d'équilibre, il détermine l'avancement à l'équilibre qui est de 39 mm. Selon la quantité initiale de calcaire introduite, il y a deux cas possibles : si la quantité initiale est inférieure à l'avancement à l'équilibre, la réaction sera totale et la quantité de matière finale de CaCO3 sera de 0. Si la quantité initiale est supérieure, l'équilibre s'établira et la quantité de matière finale de CaCO3, CaO et CO2 seront respectivement n0-xieq, xieq et xieq.
Ensuite, Mathis aborde la question suivante, où il est demandé de tracer la courbe de pression en fonction de la quantité de matière initiale introduite et de déterminer la pression finale dans l'enceinte lorsque la quantité initiale est n0. En utilisant les deux cas précédemment mentionnés et l'expression de la pression, il obtient une courbe avec une droite de pente RT/V jusqu'à xiec, puis une pression constante de xiecRT/V pour une quantité initiale supérieure ou égale à xiec.
Enfin, Mathis aborde la dernière question qui consiste à déterminer la valeur optimale de la quantité de matière initiale de calcaire à apporter. Il vérifie d'abord si la pression maximale de sécurité est respectée, ce qui est le cas avec une valeur maximale de pression de 0,35 bar. Pour privilégier un rendement optimal, il choisit la quantité de matière initiale n0 égale à xiec, qui est égale à p0Vk0/RT.
En conclusion, cet exercice aborde la dissociation du calcaire et permet d'optimiser la quantité de matière de calcaire à apporter pour obtenir le meilleur rendement de chaux vive solide. Il met en évidence l'importance de comprendre les enjeux industriels et de utiliser les outils de la chimie pour y répondre de manière optimale.
Physique-Chimie
Physique
MPSI/PCSI

Courant induit
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Physique
MPSI/PCSI

Rotation de spire
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Physique
MPSI/PCSI

Mouvement d'un aimant
Dans cette vidéo, nous examinons le mouvement d'un aimant droit de moment magnétique M, dont le pôle nord est orienté vers un circuit. Le circuit est composé d'une spire de rayon A, de centre O, d'axe OZ assimilable à une résistance R. L'aimant glisse le long de l'axe OZ à une vitesse constante V0. Le champ magnétique créé par l'aimant à une distance Z sur l'axe est donné par l'expression B = (-μ0M)/(2πZ^3).
Le sens du courant d'intensité I est déterminé par l'orientation de la surface DS. Lorsque l'aimant recule, le flux du champ magnétique augmente, ce qui induit un champ magnétique induit dans le sens opposé pour lutter contre ce phénomène. Ainsi, la norme I est strictement négative.
Pour déterminer la force électromotrice induite E, nous utilisons la loi de Faraday qui indique que E = -(dΦ/dt). En calculant le flux magnétique, on obtient Φ = -πA^3K/Z^3. En dérivant par rapport au temps, on trouve que E = -(3πA^2K)/(V0^3T^4).
Pour déterminer la valeur de Z, on utilise la loi des mailles pour établir la relation entre I et E, soit I = E/R. Cela donne I = -(3πA^2K)/(RV0^3T^4).
Lorsque l'aimant s'éloigne de la spire, le courant est négatif, ce qui est cohérent avec les résultats obtenus précédemment.
L'aspire se comporte comme un aimant avec un moment magnétique dirigé vers le bas suivant l'axe EZ. Par conséquent, elle exerce une force d'attraction sur le véritable aimant.
Si l'aimant est immobile mais proche de l'aspire, il n'y a pas de mouvement, donc pas de variation du flux magnétique, et donc pas de courant induit.
Cet exercice nous montre comment étudier le comportement d'une spire en tant qu'aimant et prédire ses effets sur le déplacement d'un aimant réel.
Physique-Chimie
Physique
MPSI/PCSI
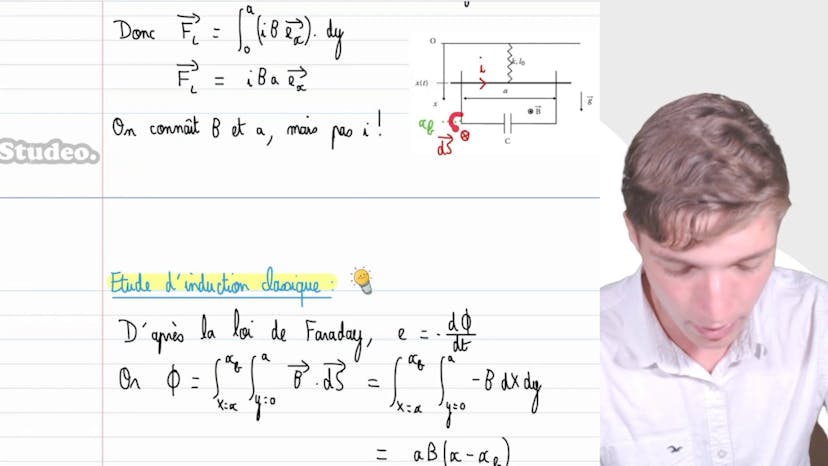
Barre et ressort
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Physique
MPSI/PCSI

Rails de Laplace
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Physique
MPSI/PCSI

Rail de Laplace + ressort
Bonjour à tous, dans cette vidéo nous étudions un dispositif de rails avec une barre attachée à un ressort. La barre a une longueur à vide L0, une constante de raideur k, une masse m, et une longueur a. Lorsque la barre est déplacée de la position d'équilibre x0 à l'instant t = 0, il y a plusieurs phénomènes qui se produisent. Tout d'abord, le ressort va déplacer la barre pour la ramener à sa position d'équilibre. Cependant, en raison du champ magnétique dans lequel se trouve le dispositif, le mouvement de la barre va créer une variation de flux magnétique à travers le circuit, ce qui génère une force de freinage qui ralentit la progression de la barre. De plus, une partie du courant induit va être dissipée par effet joule dans la résistance du circuit. Finalement, le système se stabilisera à la position d'équilibre. Le sens du courant induit dépend du sens du déplacement de la barre. Si la barre se déplace vers la droite, le courant induit va circuler dans le sens opposé. Si la barre se déplace vers la gauche, le courant induit circulera dans le sens de déplacement de la barre. En résolvant les équations électriques et mécaniques du système, nous obtenons l'équation du mouvement x'' + (1/tau)x' + (ω0^2)x = 0, avec tau = MR/AB^2 et ω0^2 = k/m. Pour avoir un régime pseudo-périodique, la résistance R doit satisfaire R < 2AB^2(ω0^2/m)^3. En résolvant cette équation, nous obtenons l'expression de x(t) =
Physique-Chimie
Physique
MPSI/PCSI

Freinage par induction
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Physique
MPSI/PCSI
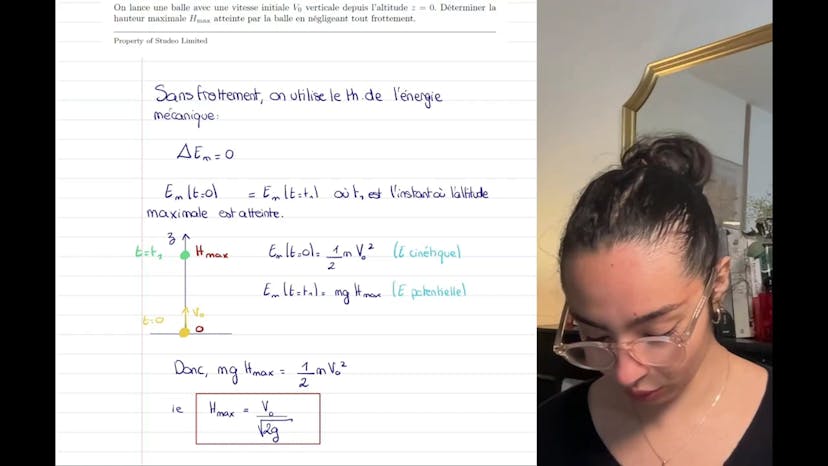
Hauteur maximale d'une balle
Dans cette vidéo, l'exercice concerne la hauteur maximale atteinte par une balle lancée verticalement avec une vitesse initiale V0 depuis une altitude z égale à 0, en négligeant les frottements.
Il y a plusieurs manières de résoudre cet exercice. La première méthode consiste à résoudre les équations horaires en appliquant le principe fondamental de la dynamique, en dérivant et intégrant ces équations pour trouver la hauteur maximale atteinte par la balle. Cette méthode est plus longue et doit déterminer à quel instant la hauteur maximale est atteinte.
Une autre méthode plus simple consiste à appliquer le théorème énergétique. Comme le mouvement est conservatif en l'absence de frottement, cela signifie que le travail mécanique est nul (ΔEM = 0). Il faut également considérer ce qui se passe aux instants t = 0 et t = 1, car le théorème de l'énergie mécanique s'applique entre deux points précis.
On peut donc dire que lorsque la hauteur maximale est atteinte à un instant t, il y a conservation de l'énergie mécanique entre ces deux points précis. À t = 0, la balle est lancée avec une vitesse verticale V0, ce qui signifie qu'elle possède uniquement de l'énergie cinétique verticale. À t = t1, l'énergie potentielle est maximale car la vitesse est nulle à ce moment-là.
On peut donc égaliser ces deux expressions d'énergie mécanique (EM) : EM à t = 0 est égale à 1/2MV0², et EM à t = t1 est égale à MGHmax (où G représente l'intensité du champ de pesanteur). En égalant ces expressions, on trouve Hmax = V0/√(2G), une formule couramment utilisée dans ce type de problèmes.
Ainsi, pour résoudre des exercices où l'on demande la vitesse, l'altitude ou autre en un point précis, la méthode du théorème énergétique est plus efficace que celle des équations horaires.
Au revoir à tous !


