Online Learning Courses

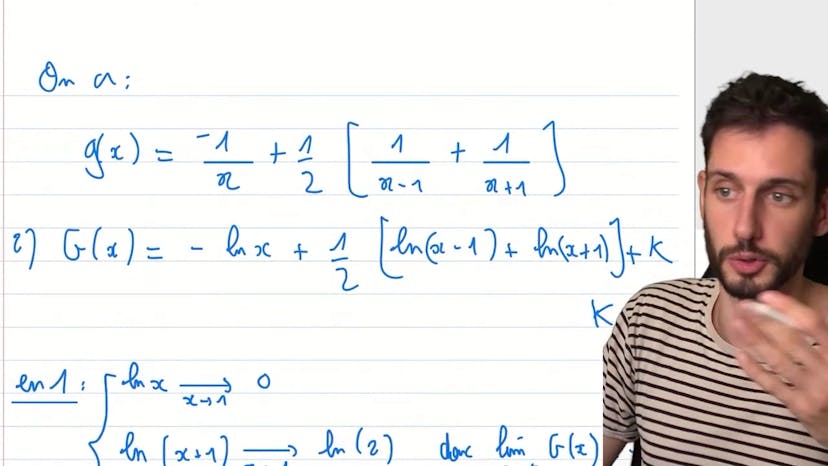
Décomposition en éléments simples

Ce cours concerne la simplification de fractions rationnelles contenant des polynômes. Il existe deux méthodes pour résoudre ces fractions, dont la méthode la plus simple consiste à mettre toutes les fractions au même dénominateur et à identifier les termes en fonction du degré du polynôme. Cependant, une méthode plus astucieuse consiste à utiliser les expressions x, x+1 et x-1 pour isoler les constantes a, b et c. Ensuite, il est possible de déterminer l'ensemble des primitives de g (la fraction rationnelle simplifiée), avec une constante k, et de trouver la limite de g en l'infini et en 1. En utilisant les propriétés des logarithmes, on peut simplifier l'expression de g et déduire que sa limite en l'infini est 0, quel que soit k.

Polynôme × exponentielle

En résumé, dans ce cours, on examine une fonction f(x) qui est un polynôme multiplié par une fonction exponentielle. On apprend que la primitive de cette fonction sera probablement un polynôme du même degré multiplié par l'exponentielle. On résout également quelques équations pour trouver les paramètres du polynôme. Finalement, on obtient l'expression de la dérivée de F(x).

Second membre en exponentielle

Les équations différentielles sont essentielles dans les études d'ingénieur. Pour résoudre une équation du premier ordre sans second membre, on divise la solution en deux parties : la solution sans second membre (SSM) et une solution particulière. La SSM est généralement de la forme exponential de x, tandis que la solution particulière dépend de la nature de la fonction Phi(x). On peut trouver la solution particulière en choisissant une fonction de la même forme que Phi(x) et en complexifiant si nécessaire. Si Phi(x) est une somme de termes, on peut séparer la solution en plusieurs parties en utilisant le principe de superposition. En résumé, pour résoudre une équation différentielle, on trouve d'abord la solution SSM puis une solution particulière en fonction de Phi(x) et on combine les deux pour obtenir la solution générale.

Solution particulière : trigonométrie

Dans ce cours, nous étudions une équation différentielle donnée. Il est suggéré de trouver une solution particulière en utilisant la forme donnée dans la question. Cependant, en essayant la forme suggérée, on se rend compte que cela ne fonctionne pas car cela produit un terme sin alors que nous avons besoin d'un terme cos. La meilleure technique est donc de combiner à la fois du cos et du sin, comme suggéré dans la question. En identifiant les termes en cos et en sin, nous obtenons les coefficients correspondants. Ensuite, nous pouvons déduire l'ensemble des solutions en ajoutant le terme correspondant à l'équation sans second membre. La solution générale est donc la somme de la solution particulière et de la solution sans second membre. C'est un principe de base dans les équations différentielles, où la recherche de la solution particulière peut être plus difficile dans les exercices plus avancés.

Solution particulière plus difficile

Dans ce cours, nous cherchons à résoudre l'équation y'-2y = xe^2x. Pour cela, nous tentons une solution particulière en utilisant une forme similaire à l'équation. Après quelques essais, nous constatons que cela ne fonctionne pas et nous devons augmenter le degré du polynôme. Nous essayons donc avec g2x et remarquons que certains termes se simplifient. Finalement, en choisissant c = 0, nous obtenons la solution y2x = k*e2x + x^2/2*e2x. Il s'agit de la solution générale de l'équation.

Théorème de comparaison - Illustration

Le théorème de comparaison en mathématiques permet d'économiser du temps et des efforts lors des démonstrations de suites. En effet, si l'on peut comparer une suite complexe à une autre plus simple et que cette dernière tend vers l'infini, alors nous pouvons conclure que la première suite aura le même comportement. Ce théorème est utile quand une suite est compliquée à démontrer et qu'on peut la comparer à une autre plus simple. Ainsi, le théorème permet de passer outre les démonstrations complexes en utilisant des suites plus simples. Dans la prochaine vidéo, nous verrons comment ce théorème peut être utilisé.

Théorème de comparaison - démonstration

Ce cours explique comment démontrer le théorème de comparaison en utilisant la divergence vers plus infini. Pour cela, il faut revenir à la définition de TvPi pour une suite et traduire la limite de Un égale plus infini. Ensuite, on peut conclure que Vn est plus grand ou égal à Un, plus grand ou égal à A pour tout A positif et N plus grand ou égal à un certain grand N de la suite. En résumé, cette démonstration permet d'éviter l'utilisation des démonstrations en epsilon ou en grand A, et de simplifier les exercices de comparaison.

Théorème des gendarmes

Le théorème d'encadrement, ou théorème des gendarmes, permet de montrer qu'une suite va tendre vers un réel fini en encadrant la suite entre deux autres suites convergentes vers la même limite. Le recours à ce théorème combiné au théorème de comparaison peut permettre d'accéder à des résultats sur les suites sans se préoccuper des définitions formelles d'epsilon et de A. Pour illustrer le théorème d'encadrement, on peut prendre l'exemple de la suite sinus s sur n encadrée par les suites des 1 sur n et des "-1 sur n". Si deux suites ordonnées convergent, alors leurs limites seront également ordonnées. Ce théorème est utile en mathématiques même si toutes les situations ne sont pas aussi simples à résoudre que celle de l'exemple.

Suite majorée, minorée & Th de convergence monotone

Dans ce cours, le professeur explique les concepts de majoration, de minoration et de bornage des suites. Une suite est dite majorée lorsqu'elle est bloquée par une certaine valeur et ne peut pas dépasser cette valeur. Il peut y avoir plusieurs majorants pour une suite. De même, une suite est dite minorée lorsqu'elle ne peut pas descendre en dessous d'une certaine valeur. Une suite est dite bornée lorsque elle est à la fois majorée et minorée. Le professeur illustre ces notions à l'aide de quelques exemples de suites bornées. Il mentionne le théorème de convergence monotone, qui associe le fait d'être croissante à celui d'être majorée. Ce théorème permet de conclure que si une suite est croissante et majorée, alors elle converge. Cependant, il précise que ce théorème ne donne pas la valeur de la limite de la suite. Le professeur présente également la version du théorème de convergence monotone pour les suites décroissantes et minorées, ainsi que pour les suites croissantes et non majorées, et les suites décroissantes et non minorées. Il insiste sur le fait que la réciproque du théorème de convergence monotone est fausse, c'est-à-dire que converger ne signifie pas forcément être croissante majorée ou décroissante minorée. Il donne des contre-exemples pour illustrer ce point, notamment la suite sinus sur n qui converge vers 0 mais oscille de manière "moche". Enfin, il conclut en soulignant l'importance de ne pas se laisser piéger par des fausses idées sur les suites qui convergent. N'hésitez pas à consulter la FAQ ou à discuter avec les autres étudiants si vous avez des questions.

Th convergence monotone - démo

Le théorème de convergence monotone prouve que toute suite croissante et non majorée tend vers l'infini. Il suffit de trouver un certain rang à partir duquel la suite est toujours au-dessus d'un nombre fixe A. Comme la suite n'est pas bloquée, il existe un anti-naturel P où la suite dépasse A. En combinant cela avec le fait que la suite est croissante, on peut montrer que pour tout A fixé, la suite finit toujours par être au-dessus de ce A. Cela prouve la convergence monotone.

Limite finie

Dans cette vidéo, nous abordons la notion de limite réelle en mathématiques. La limite réelle est la valeur vers laquelle une suite converge intuitivement lorsque n augmente. Pour être plus précis, nous utilisons la notion de couloir. Dans cette vidéo, nous expliquons ce qu'est un couloir autour de la limite et montrons qu'une suite peut converger de manière douce (croissance ou décroissance) ou chaotique. Officiellement, on dit qu'une suite UN converge vers un réel L si tout intervalle autour de L (incluant L) finit par contenir tous les termes de la suite à un certain moment. Pour illustrer cela graphiquement, nous utilisons un graphique représentant la suite et un couloir de taille variable autour de la limite (2 dans cet exemple). Nous vérifions si tous les termes de la suite sont inclus dans le couloir à partir d'un certain moment. Si cela est vrai pour toutes les tailles de couloir, alors la limite est valide. Nous illustrons ensuite cette idée en réduisant la taille du couloir de plus en plus. Si tous les termes de la suite sont inclus dans le couloir à partir d'un certain moment, cela signifie que les termes de la suite se rapprochent de plus en plus de la limite (2 dans cet exemple), indépendamment de la taille du couloir. Nous démontrons également que cette notion de convergence peut s'appliquer à des suites croissantes, décroissantes ou oscillantes autour de la limite. En résumé, cette vidéo explique la notion de limite réelle en mathématiques en utilisant la notion de couloir pour illustrer graphiquement cette idée. Nous montrons également que les suites peuvent converger de différentes manières vers leur limite, que ce soit de manière croissante, décroissante ou oscillante.