 All subjects
All subjects
 All subjects
All subjects
Physique-Chimie
Physique
Terminale

Intensité du courant
Dans cette vidéo, Mathias de Studio nous explique les systèmes capacitifs en commençant par la notion d'intensité du courant.
Il présente un exercice d'introduction qui consiste à analyser la charge électrique traversant une section de conducteurs. La charge augmente linéairement au fil du temps.
Ensuite, Mathias explique comment relier l'intensité du courant à la charge traversant une section du conducteur. L'intensité du courant est définie comme la charge des porteurs divisée par la durée considérée.
Il souligne que plus le nombre de charges est élevé, plus l'intensité du courant sera importante.
Enfin, Mathias fait une application numérique en prenant l'intervalle de 0 à 4 millisecondes et en utilisant la valeur maximale de charge traversant le conducteur (6 millicoulons). Il obtient ainsi un courant de 1,5 ampère, ce qui est dans les ordres de grandeur usuels pour des appareils électroménagers.
Il conclut en rappelant l'importance de retenir la définition de l'intensité du courant pour comprendre les systèmes capacitifs et en propose de passer à d'autres notions par la suite.
Physique-Chimie
Physique
Terminale
Capacité d’un condensateur
Aucun résumé n'est disponible pour cette vidéo
Physique-Chimie
Physique
Terminale
Équation différentielle
Dans cette vidéo, on étudie l'établissement d'une équation différentielle à partir d'un système capacitif. On part d'un condensateur déchargé qui est placé en série avec une résistance. L'interrupteur est fermé à t=0 et on utilise la loi des mailles pour établir une relation entre les tensions UC, UR et UE.
On repère dans le schéma un générateur de tension qui impose une tension E à travers le circuit, une résistance R avec une tension UR et un condensateur avec une tension UC. En utilisant la loi des mailles, on fait un tour dans le circuit en comptant les tensions dans le sens dans lequel elles arrivent. On obtient ainsi l'équation UC + UR = E.
Ensuite, on remplace la tension UR en utilisant la loi de Ohm, qui dit que la tension aux bornes d'une résistance est égale à R fois le courant. On obtient donc UR = R * I, où I est le courant qui passe à travers la résistance. On substitue cette expression dans l'équation précédente, ce qui donne UC + R * I = E.
On nous dit que I = C * (dUC/dt), où C est la capacité du condensateur et dUC/dt est la dérivée temporelle de la tension UC. On remplace I par cette expression et on obtient UC + RC * (dUC/dt) = E.
Finalement, on a une équation différentielle vérifiée par la tension UC, qui est la dérivée temporelle de UC plus RC fois UC égal à une constante, E/RC. Cette équation différentielle peut être résolue ensuite.
En conclusion, cet exercice met en évidence comment établir une équation différentielle à partir d'un système capacitif en appliquant la loi des mailles et en utilisant des variations telles que la loi de Ohm. C'est une compétence fondamentale en électrotechnique.
Physique-Chimie
Physique
Terminale

Circuit RC
Dans cette vidéo, nous nous intéressons à l'équation différentielle qui régit un circuit RC. Un circuit RC est composé d'un condensateur de capacité C en série avec une résistance R et d'un générateur de force électromotrice E.
L'équation différentielle qui régit la tension UC au niveau du condensateur lors de la charge est donnée par RC * d2UC/dt + UC = E. On doit vérifier si l'expression UC = A + B * exp(-t/RC) est une solution de cette équation et trouver la valeur de A.
Pour vérifier cela, nous devons dériver UC. Nous dérivons donc A et obtenons simplement 0, puis la dérivée de l'exponentielle est -1/RC. Ainsi, nous avons la dérivée du facteur dans l'exponentielle qui est -1/RC * B * exp(-t/RC).
En injectant UC et sa dérivée dans l'équation, on obtient RC * d2UC/dt + UC = A + B * exp(-t/RC) + (-1/RC * B * exp(-t/RC)).
D'après l'énoncé de l'équation, on sait que cela est égal à E. Donc, on peut conclure que UC est une solution de l'équation lorsque A = E.
La deuxième question consiste à trouver l'expression de B lorsque le condensateur est initialement déchargé. Dans ce cas, UC(0) = 0. En évaluant UC(0) dans l'expression UC, on a donc 0 = E + B. Donc, on en déduit que B = -E, et on obtient finalement l'expression UC = E * (1 - exp(-t/RC)).
Dans le cas où le condensateur est chargé initialement à une tension U0 inférieure à E, la seule différence est que UC(0) = U0. En suivant les mêmes étapes, on trouve que B = U0 - E, et l'expression de UC est UC = E + (U0 - E) * exp(-t/RC).
Enfin, sur le même graphique, on peut représenter l'allure des fonctions UC(t) dans les deux cas précédents. Dans les deux cas, UC tend vers E à l'infini, et la durée caractéristique pour atteindre le régime permanent est RC. La seule différence réside dans la valeur initiale à l'origine, qui dépend si le condensateur est chargé ou déchargé initialement.
Cette vidéo présente donc la résolution de l'équation différentielle associée à la tension au niveau du condensateur dans un circuit RC. C'est une méthode classique à connaître pour comprendre les phénomènes qui se produisent dans ce type de circuit.
Physique-Chimie
Physique
Terminale
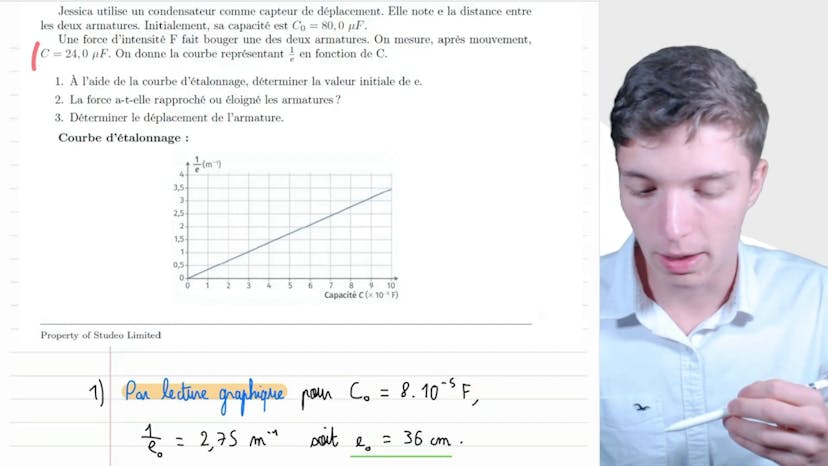
Capteur de déplacement
Dans cette vidéo, Jessica utilise un condensateur comme capteur de déplacement. Initialement, la capacité du condensateur est de 80 µF, mais après mouvement, elle mesure une capacité de 24 µF. La courbe représentant 1/E en fonction de C est donnée pour aider à étalonner la valeur initiale de E. En utilisant cette courbe, il est possible de déterminer que la distance initiale entre les deux armatures était de 36 cm.
En observant l'évolution de la capacité, il est clair que la capacité a diminué, ce qui signifie que la force a éloigné les deux armatures. La capacité étant inversement proportionnelle à E, une diminution de la capacité entraîne une augmentation de E. Donc, la force a effectivement éloigné les armatures et réduit la capacité du condensateur.
Maintenant, l'objectif est de déterminer le déplacement de l'armature. En partant de la capacité finale, qui est de 0,8 mètres moins 1, on peut conclure que l'espacement final est de 1,3 mètres. En soustrayant l'espacement initial, on obtient un déplacement ΔE de 94 cm.
Il s'agit donc d'un exercice intéressant qui montre comment utiliser un condensateur pour créer un capteur de déplacement. En utilisant une relation linéaire simple, il est possible de raisonner posément et d'obtenir une réponse fluide. Merci d'avoir suivi cette vidéo et à bientôt !
Physique-Chimie
Physique
Terminale

Lampe rechargeable
Dans cette vidéo, Mathis présente une lampe rechargeable à base d'un système capacitif. Cette lampe utilise l'énergie mécanique du mouvement pour se recharger et stocke cette énergie dans un condensateur de capacité de 4 Farad. Une fois le condensateur chargé, la tension à ses bornes est de 5,5 volts. Un mouvement de 30 secondes permet à la lampe de fonctionner pendant quelques minutes. Pour étudier le comportement en décharge du condensateur, celui-ci est associé à un conducteur ohmique de résistance 220 ohm et à un interrupteur. Lorsque l'interrupteur est fermé, la tension aux bornes de la lampe est de 2 volts. En utilisant ces données, Mathis schématise le circuit électrique de décharge du condensateur. Ensuite, il détermine l'expression du courant en fonction du temps en calculant la dérivée temporelle de la tension aux bornes du condensateur. Cela permet de trouver que l'intensité du courant est égale à C/tau * (E - U_seuil) * exp(-t/tau), où C est la capacité du condensateur, tau est la constante de temps du circuit RC, E est la tension initiale du condensateur et U_seuil est la tension seuil de la LED. Mathis explique ensuite que pour que la LED fonctionne correctement, le courant doit être supérieur à 10 mA. Il en déduit une inéquation qui permet de trouver la durée de fonctionnement prévue. En résolvant cette inéquation, il obtient une condition sur le temps qui doit être inférieur à -tau * ln(tau * I_min / (c * (E - U_seuil))), où I_min est le courant minimal de fonctionnement, c est la capacité du condensateur et E - U_seuil est le facteur d'exponentielle de la formule précédente. En effectuant les calculs numériques, Mathis trouve que la durée d'utilisation de la lampe est de 409 secondes. Il conclut en soulignant la manipulation mathématique complexe de cet exercice, mais aussi l'importance de comprendre les concepts physiques et électroniques sous-jacents.
Physique-Chimie
Physique
Terminale
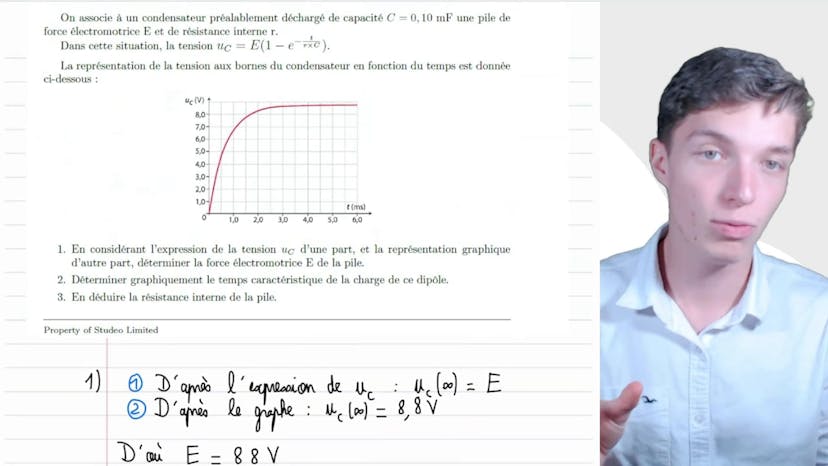
Caractéristique d’une pile
Dans cette vidéo, il est question de la caractéristique d'une pile associée à un condensateur déchargé. La tension UC de ce circuit est donnée par l'expression UC = E*(1 - e^(-1/RC)), où E est la force électromotrice de la pile.
Pour déterminer la valeur de E, on peut simplifier cette expression en regardant la valeur de la tension UC à l'infini. En observant le graphique, on constate que la tension converge vers une valeur particulière, qui est environ 8,8 volts. Donc E est égale à 8,8 volts.
Ensuite, il est demandé de déterminer graphiquement le temps caractéristique de la charge du condensateur. Le temps caractéristique correspond au temps auquel la tension atteint 0,63 fois sa valeur maximale. En repérant cette valeur sur le graphique, on trouve que le temps caractéristique est d'environ 0,6 millisecondes.
Enfin, on nous demande de déduire la résistance interne de la pile. En utilisant la relation Tau = RC, où Tau est le temps caractéristique et C est la capacité du condensateur, on peut trouver que la résistance interne R est égale à Tau/C, soit environ 6 Ohm.
En conclusion, dans cette vidéo, on a utilisé l'expression de la tension UC et le graphique de l'évolution de cette tension pour déterminer la valeur de la force électromotrice de la pile, le temps caractéristique et la résistance interne de la pile.
Physique-Chimie
Physique
Terminale

Balance
Dans cette vidéo, Matisse de Studio explique comment on peut utiliser un condensateur comme balance. Le condensateur comporte une armature mobile et une fixe reliée par des ressorts de raideur k. Au départ, le condensateur a une capacité de 39 nF et une distance de 7,9 cm entre les armatures. On pose ensuite une masse m sur la coupole, ce qui réduit la distance entre les armatures. Cela entraîne une augmentation de la capacité du condensateur, mesurée à 73 nF. En utilisant la relation C x E = 3.1 x 10-9 F.m, on trouve que la distance finale entre les armatures est de 4.2 cm. En utilisant la relation m = k(E0-E)/g, on peut calculer la masse m qui a été posée, soit 27 g. Ce cours met en évidence la façon dont les connaissances en physique peuvent être utilisées pour comprendre et mesurer des objets du quotidien, comme une balance.
Physique-Chimie
Physique
Terminale
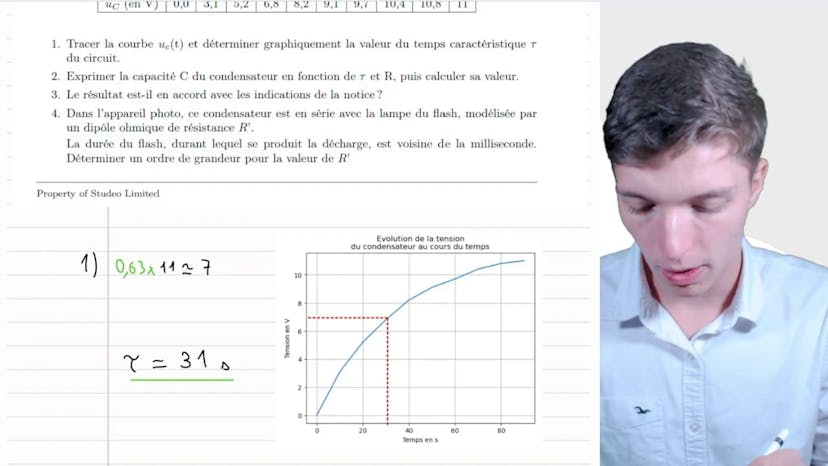
BAC: Flash
Dans cette vidéo, l'objectif est de vérifier la valeur d'un condensateur utilisé dans le flash d'un appareil photo. La capacité du condensateur est donnée dans la notice comme étant de 150 µF, avec une tolérance de plus ou moins 10%. Pour vérifier cette valeur, le condensateur est inclus dans un circuit électrique avec un dipôle ohmique de résistance 0,25 MΩ, un générateur de tension continue de 12V et un interrupteur ouvert. Après avoir refermé l'interrupteur, la tension aux bornes du condensateur est mesurée toutes les 10 secondes.
La première question consiste à tracer la courbe de la tension (UC) en fonction du temps et de déterminer la valeur du temps caractéristique (taux) du circuit. Pour cela, il faut repérer le moment où la tension atteint 0,63 fois sa valeur finale (ici, 0,63 * 11V ≈ 7V). En observant la courbe, on constate que cela se produit au bout d'environ 31 secondes.
En utilisant la formule taux = RC, où R est la résistance et C est la capacité du condensateur, on peut exprimer la capacité du condensateur en fonction du temps caractéristique et de la résistance. En utilisant cette formule, on trouve une capacité de 124 µF pour le condensateur.
On peut alors vérifier si ce résultat est en accord avec les indications de la notice. La notice spécifie une capacité de 150 µF ± 10%. Étant donné que la valeur mesurée est de 124 µF, le condensateur est en contradiction avec la notice car sa capacité est trop faible.
Dans l'appareil photo, le condensateur est en série avec la lampe du flash, modélisée par un dipôle ohmique de résistance R'. La durée du flash est d'environ une milliseconde. Le but est donc de déterminer un ordre de grandeur pour la valeur de R'. En utilisant la relation taux prime = c * R', où taux prime est le temps caractéristique pour le flash, on peut exprimer R' en fonction de taux prime et de la capacité. En effectuant les calculs, on obtient une valeur de R' égale à 8 Ohm.
En conclusion, cet exercice vise à vérifier si la valeur du condensateur correspond aux indications de la notice. Il est recommandé d'utiliser des méthodes de vérification, telles que le calcul des marges d'erreur, pour interpréter les résultats. Ce type d'exercice est courant dans les examens scolaires et implique des notions relativement simples. En utilisant les méthodes adéquates, il est possible de déterminer si une valeur est conforme ou non à des spécifications données. Merci d'avoir regardé la vidéo et à bientôt.
Physique-Chimie
Physique
Terminale
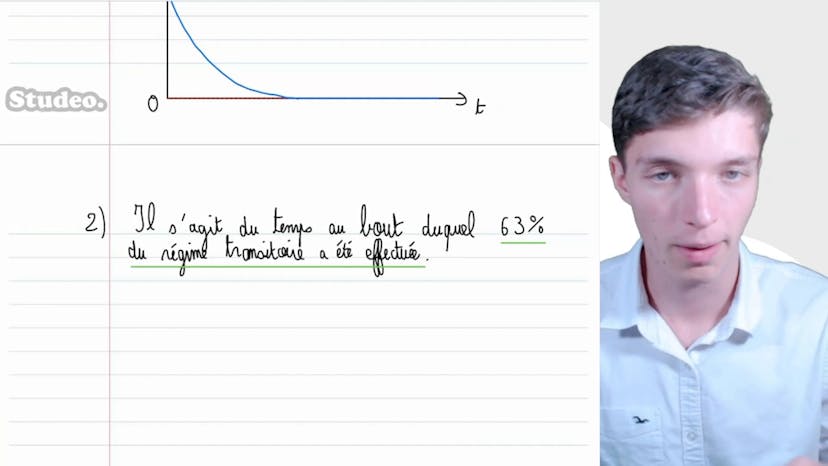
BAC : Décharge d’un condensateur
Dans cette vidéo, nous étudions la décharge d'un condensateur. Le condensateur est initialement chargé sous une tension U0 de 10V. L'intensité du courant traversant le condensateur est notée I et la charge positive de l'armature A est notée Q.
Pour commencer, nous établissons la relation entre I et UC, la différence de potentiel aux bornes du condensateur. D'après la relation tension-courant pour un condensateur, on a I(t) = C * dUC/dt.
Ensuite, nous montrons que l'équation différentielle régissant l'évolution de UC est donnée par α * UC + dUC/dt = 0, avec α = 1/RC où R est la résistance et C la capacité du condensateur.
Nous trouvons ensuite la solution de cette équation différentielle, qui est UC(t) = U0 * exp(-α * t). Nous dessinons le graphique de cette solution, montrant que la tension à l'infini est nulle.
Nous déterminons ensuite le temps caractéristique de décharge du condensateur, qui est égal à RC. En utilisant ce temps caractéristique et la résistance de 330 kOhm, nous calculons la capacité du condensateur qui est de 0,27 µF.
Enfin, nous montrons que l'intensité du courant est égale à -U0/R ou à -t/RC, en utilisant l'expression de UC obtenue précédemment. Nous calculons la valeur de UC et I à t = 0,5 secondes et concluons que le condensateur est déchargé à cet instant.
Cet exercice nous permet d'appliquer les différentes méthodes vues en cours sur les circuits RC. Il n'y a pas de pièges particuliers, il suffit de bien comprendre les concepts et d'appliquer les formules appropriées.
Physique-Chimie
Physique
Terminale

Équation des gaz parfaits
Dans cette vidéo, Mathis du studio explique l'équation d'état d'un gaz parfait. L'équation d'état pour les gaz parfaits est p * v = n * r * t, où p est la pression, v est le volume, n est la quantité de matière, r est la constante des gaz parfaits et t est la température. La constante des gaz parfaits, r, vaut 8,314 pascal mètre cube par mol par kelvin.
Il explique également que la température en kelvin est équivalente à la température en degrés plus 263 unités.
L'équation d'état permet de calculer la pression d'un gaz parfait si on connaît son volume molaire, la quantité de matière, et sa température. Elle permet également de déduire d'autres grandeurs si on connaît certaines caractéristiques du gaz.
Il utilise l'exemple d'un gaz parfait avec un volume molaire de 23 litres par mol à 15 degrés. En utilisant la formule P = R * T / (V * N), où P est la pression, R est la constante des gaz parfaits, T est la température, V est le volume et N est la quantité de matière, il trouve que la pression est égale à 1,04 bar.
Il souligne l'importance de faire attention aux unités utilisées et aux grandeurs qui sont fixées ou non lors de l'utilisation de cette équation.
Physique-Chimie
Physique
Terminale

Énergie interne
Dans cette vidéo, nous étudions l'énergie interne d'un système thermodynamique, en se concentrant sur l'échauffement d'une plaquette de frein lors d'un freinage. Il est important de définir le système d'étude et d'identifier le milieu extérieur. Le système d'étude est la plaquette de frein elle-même, car c'est ce qui nous intéresse. Le milieu extérieur est le reste de la voiture et peut également inclure le sol ou l'air. L'énergie interne est une notion subtile en thermodynamique. Contrairement à la mécanique, qui utilise les énergies potentielles et cinétiques, l'énergie interne correspond à l'agitation thermique des particules dans le système. Elle est définie comme la somme des énergies de vibration des molécules qui composent le système. Cette définition est importante à connaître car l'énergie interne est largement utilisée dans la thermodynamique. Merci d'avoir regardé cette vidéo et à bientôt !


