All subjects
All subjects
 All subjects
All subjects
La formule des probas totales
La formule des probabilités totales est une formule très importante en statistiques. Pour l'expliquer, prenons un exemple concret d'un lycée où il y a des garçons et des filles, et des blonds et des bruns.
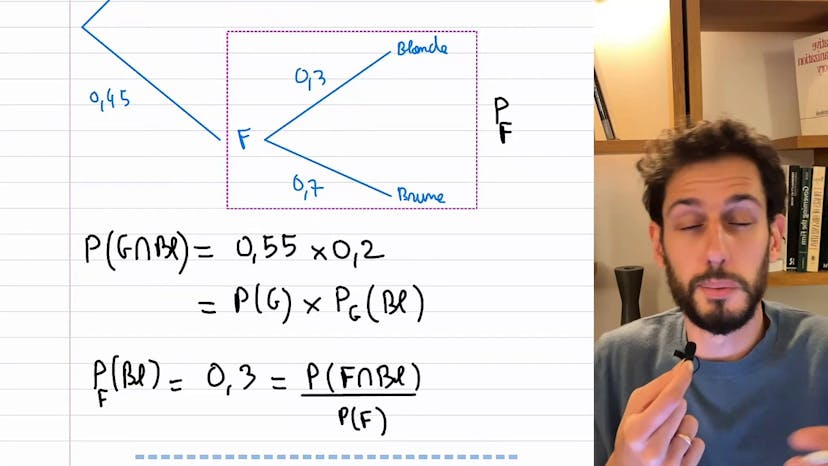
La probabilité d'être à la fois blond et garçon est simplement la probabilité d'être un garçon multipliée par la probabilité d'être blond (une fois qu'on a dit qu'on est un garçon).
Maintenant, intéressons-nous à la probabilité d'avoir les cheveux blonds dans ce lycée. Imaginons qu'il y ait 100 personnes : 55 garçons et 45 filles. Si je tire une personne au hasard, quelle est la probabilité qu'elle ait les cheveux blonds, qu'elle soit un garçon ou une fille ?
L'idée ici est de ne pas se focaliser uniquement sur les blonds, mais plutôt sur les deux aspects (garçon et blond). La probabilité d'être blond peut être atteinte en suivant deux chemins possibles : soit j'ai tiré un garçon blond, soit j'ai tiré une fille blonde. La formule des probabilités totales consiste à sommer ces deux probabilités pour obtenir la probabilité d'être blond.
En d'autres termes, pour trouver la probabilité que quelqu'un soit blond, je repère tous les endroits dans mon arbre qui correspondent à cet événement, c'est-à-dire être blond. Ensuite, je somme toutes les probabilités qui y conduisent.
La formule des probabilités totales peut être exprimée de deux façons : soit la somme des deux probabilités avec le signe '+', soit en utilisant la formule des probabilités conditionnelles.
En théorie, si nous avons une partition de l'univers, la probabilité d'un événement B peut être calculée en cherchant B dans chacune des branches et en les sommant toutes.
La formule des probabilités totales est donc la somme des probabilités de chaque branche contenant l'événement B. On peut également utiliser la formule des probabilités conditionnelles pour chaque élément.
L'intuition derrière cette formule est de chercher où se trouve l'événement dans chaque branche et de sommer toutes ces probabilités.
J'espère que cela a été clair pour vous. N'hésitez pas à laisser des commentaires si vous avez des questions, et à bientôt pour une prochaine vidéo. Au revoir !