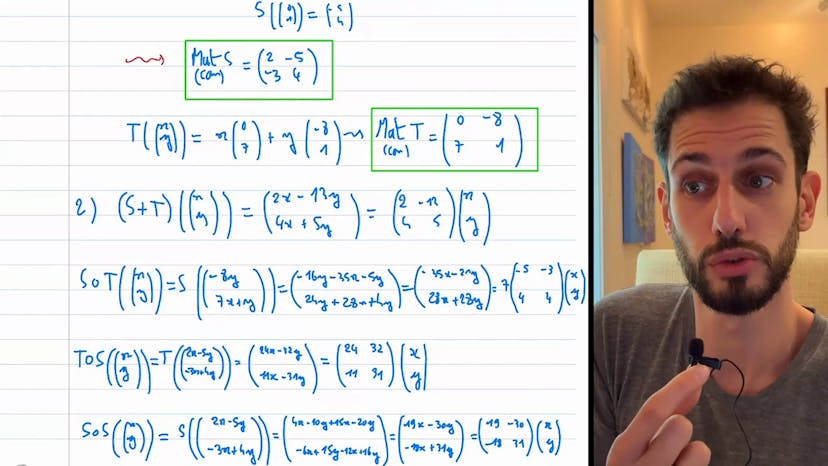Home

MPSI/PCSI

Maths

Algèbre

Matrices applications linéaires 

Le cours porte sur plusieurs notions en mathématiques, notamment la détermination du noyau et de l'image d'une application linéaire, ainsi que le calcul de puissances d'une matrice. L'auteur utilise une matrice spécifique, notée F, pour illustrer ces concepts.

Dans un premier temps, l'auteur propose de calculer les puissances M² et M³ de la matrice F. Ensuite, il s'intéresse aux images et aux noyaux de M² et F². Pour cela, il utilise l'observation et la combinaison linéaire des vecteurs de la matrice.

Ensuite, l'auteur utilise une méthode alternative en utilisant une matrice de passage associée à l'application linéaire F. Il calcule les composantes des vecteurs de base E1, E2 et E3 après l'application de F. Il en déduit l'image de F et le noyau de F.

Dans la suite du cours, l'auteur explique qu'il est possible de prédire que la puissance M³ pourrait être nulle, mais il effectue quand même le calcul pour confirmer ce résultat. Il conclut en donnant des astuces pour certains calculs, notamment lorsque l'on a des polynômes comme 1-x².

Enfin, l'auteur recommande de s'entrainer sur ce genre d'exercices pour mieux comprendre les liens entre application linéaire et matrice. Il encourage également les questions et les échanges pour approfondir ces concepts mathématiques.

un exercice assez complet qui reprend pas mal de techniques qu'on a déjà vu, soit F, un endomorphisme de R3 dont la matrice est la suivante. On va déterminer premièrement un calcul, on va trouver ensuite le noyau et l'image, peut-être que le calcul nous aidera à aller plus vite. Calculer M², M³, ensuite on va chercher l'image et le noyau de M², enfin de F², mais on va sûrement céder à la question d'avant, et on va ensuite faire un truc genre calculer un certain quelque chose ici, puis on va voir ce que c'est. Donc tout ça c'est extrêmement classique, notamment la dernière question, il faudra savoir refaire ça à part que allons-y, on fait ça en détail. Donc F de 2E1-3E2 plus 5E3, deux méthodes pour le faire, soit je fais un calcul matriciel où je fais M fois 2-3, 5, voilà, soit j'utilise la linéarité et je calcule 2F2-3F2E2 plus 5F2E3. Je vous fais les deux pour vous montrer que c'est la même chose, c'est parfaitement équivalent, donc si je fais M fois 2-3-5, je fais 2 fois 2, moins 3 fois 1, 0 fois 5, ça fait 4-3, ça fait 1, etc. Voilà, je fais le calcul, ou bien je prends 2F2E1, donc 2 fois ça, plus moins 3 fois ça, plus 5 fois ça, parce que F2E1 c'est ça, F2E2 c'est ça, F2E3 c'est ça, et quand je le fais, ça donne la même chose. Voilà, très facile. Déterminer le noyau de F et l'image de F. Alors, on va appliquer la technique un peu observation, c'est-à-dire soit soit la matrice est inversible, F est bijective, et donc imF est de dimension 3. C'est possible, soit imF est de dimension 2. Pourquoi ? Parce que j'observe que ces deux vecteurs-là, je prends toujours les deux premiers, je regarde, les deux premiers, ou les deux derniers, voilà, j'en trouve deux facilement, qui sont indépendants. Donc, s'ils sont indépendants, j'ai au moins imF de taille 2. Je me demande s'il est de taille 3, et je me dis, bah, s'il n'est pas de taille 3 et qu'il est de taille 2, je vais pouvoir trouver des combinaisons linéaires, donc je cherche un 0, et je m'amuse à faire, ok, recombiner les autres vecteurs pour faire apparaître un 0 au niveau de la troisième coordonnée, et voir si je peux exprimer une combinaison facilement. Donc tout de suite, j'ai envie d'essayer de faire ça, plus ça, puisque 1 moins 1 fait 0, je vais sommer ces deux vecteurs, je vais faire F2E1 plus F2E3, et donc, quand je fais ça, F2E1 plus F2E3, je me rends compte que ça fait exactement 2 moins 2, 0. C'est parfait, ça fait exactement deux fois le vecteur du milieu. Donc, j'ai trouvé une combinaison linéaire, ça veut dire que imF est bien égal à vect de tout ça, pourquoi ? Parce que vect, les deux premiers vecteurs de la matrice, est inclus dans imF, et grâce au fait que j'ai trouvé une combinaison linéaire entre les trois vecteurs, je sais qu'imF n'est pas égal à 3. Donc imF égal à 2, d'im de imF, pardon, excusez-moi, donc d'im de imF est inférieur strict à 3, donc elle est soit égale à 1, soit égale à 2, et j'ai un espace qui est de taille 2 inclus dans imF. Forcément, imF est de taille supérieur égale à 2, plus petit strict que 3, et de taille 2, les deux espaces sont donc égaux. Voilà. Et ensuite, j'utilise cette combinaison linéaire intelligente que je viens de trouver pour aussi trouver le quart F. Pourquoi ? Parce que ça c'est une combinaison linéaire en fait entre F de E1, F de E2, F de E3, pardon, ça c'est F de E3, ça c'est F de E2, je vais utiliser cette combinaison linéaire et la réécrire avec les F. J'ai F de E1 plus F de E3 égale 2 F de E2. Ça, ça s'écrit en fait, il y a une table intermédiaire que j'ai pas écrite, mais ça, ça s'écrit F de E1 plus E3 moins 2 E2 égal à 0. Et E1 plus E3 moins 2 E2, c'est 1 moins 2, 1. Je trouve que ça est égale à 0, donc je trouve que le vect de ça est inclus dans le noyau. Le noyau est de taille 1 par le théorème du rang. J'ai donc, en appliquant à peu près le même raisonnement qu'au-dessus, le fait que j'ai un élément dans le noyau qui est de même taille que le noyau, de même dimension je veux dire, donc par le théorème du rang, donc je peux déduire que le noyau c'est ça. Par l'observation, sans faire les techniques de calcul du genre résoudre M3 grand I X égal à 0, je trouve noyau et image. On est content, c'est bien. Calculer M2, calculer M3, en général dans ces exos, par habitude je vous le donne comme ça comme astuce de méta-vision à l'avance, on peut s'attendre qu'il y ait, je sais pas, 30% de chances que M3 soit nul. Des fois on fait monter les puissances comme ça de manière un peu, on sait pas trop pourquoi, le carré et le cube. Souvent c'est parce que, comme par hasard, il y en a une qui sera nulle. Bon, je le fais quand même le calcul. M2 et M3, on en le produit, donc c'est parti. M2, je trouve ça. Je vois que M2 est déjà de rang 1, parce que c'est trois mêmes vecteurs, donc l'image de M2 c'est juste le long d'un seul vecteur. M3, je fais le calcul, je trouve 0. Deuxième méthode pour calculer M2, je pourrais aussi dire que M2, c'est associé à F1F, donc je pourrais calculer F1F de E1, E2, E3. Je le fais pour vous montrer différentes méthodes. Comme F1F, F2E2, F2E3 sont égales à ça, je peux calculer F1F de E1, F1F de E2, F1F de E3, c'est un peu laborieux, mais on s'en sort. Et on retrouve au final cette matrice, regardez. 1-2, 1, 1-2, 1, 1-2, 1. Si on fait pareil pour F3, ça va très vite. Je me rends compte que F3 de E1 va donc être égal à F3 de E2, donc être égal à F3 de E3, parce que les trois sont les mêmes. Et donc ça sera égal à F2 du premier, moins 2F2 du deuxième, plus F2 du troisième. Et quand je fais ça, je me rends compte que c'est ça une fois, plus ça une fois, moins deux fois ça, ça fait bien 0. En gros, ça s'arrange dans les deux cas. Je pense que le calcul matriciel est plus bienvenu ici, mais bon, les deux sont possibles. Donc, question d'après, on vous dit déterminer noyau et image. J'ai déjà un petit peu fait à l'oral. M2, c'est ça. Image, vect de 1-1, direct. Noyau, il faut que je trouve quelque chose de dimension 2, vu qu'en gros j'ai un théorème du rang qui me dit que si l'image est de dimension 1, le noyau est de dimension 2. Donc je trouve deux éléments qui se font envoyer sur 0. Je vais vous montrer comment on fait. L'hymne, c'est ça. Le noyau, il faut observer. Vu que la matrice de M2, j'ai écrit M2, vu que M2, c'est ça. Je me rends compte que si je prends ce vecteur moins celui-là, ça fait 0. Ce vecteur moins celui-là, ça fait 0. J'ai trouvé F2-E2, F2-E2, F2-E2-F2-E3, qui sont des éléments du noyau. Sauf que F2-E1-E2, ça revient à dire que F2-1-1, 0. Ça c'est E1-E2, égal 0. Et ici j'ai F2-E1-E3, 1, 0, moins 1. Ça c'est égal à 0. Et je me rends compte que ces deux éléments, 1-1, 0 et 1, 0, moins 1, sont indépendants. Le vecteur de ces deux éléments est de dimension 2, il est inclus dans le noyau. Le noyau est de dimension 2, les ensembles sont égaux. Très vite, quand j'ai trouvé ça, par observation, je trouve comme ça deux éléments, E1-E2, E1-E3, dont la combinaison fait 0, donc ça veut dire des éléments qui se font envoyer sur 0 par F, ça me donne le noyau. Le raisonnement c'est, je connais sa dimension, je trouve deux éléments indépendants, j'ai l'ensemble. Et enfin, petit 5, calculez ça. Alors ça, très classique, je vous le dis tout de suite, quand vous voyez du 1-x fois 1 plus x plus x², tout de suite, systématiquement, vous pensez somme géométrique. C'est la somme des termes d'une suite géométrique de première. Ici, c'est juste appliqué à une matrice. Donc voilà, il ne faut pas hésiter, quand vous voyez ça, c'est toujours la même chose. Donc là on fonce, on écrit, somme géométrique, ça fonctionne pourquoi ? Parce qu'en fait, vous avez un produit avec que du i et du m, donc tout ça, c'est des éléments qui commutent. M commute avec elle-même, tout commute avec i, donc il n'y a pas trop de problème de produit de matrice. Donc vous calculez, vous faites le calcul, avec la formule géométrique. Donc la formule géométrique, c'est quoi ? Vous la connaissez, je la mets ici, je vous la mets là, vous pouvez la connaître par cœur. C'est 1-q fois 1 plus q plus qn égale 1-q puissance n plus 1 sur 1-q. Non, pardon, égale 1-q puissance n plus 1, voilà. C'est le truc de première. Là, vous l'avez, vous faites le calcul, ça fait i-m fois i plus m plus m2 égale i-m3. On vient de démontrer que m3 était nul, le tout fait i. Conclusion, j'ai un produit où j'ai i-m fois quelque chose égale i. Par définition, j'ai trouvé une matrice qui, quand j'ai multiplié par i-m fait i, c'est l'inverse de i-m. Donc, boum, ça vous donne i-m est inversible. Son inverse est ce truc-là. Voilà, ultra classique, posez des questions si vous en avez. C'est le genre d'exos qui se fait très bien avec de l'expérience. Au début, vous pouvez le faire aussi d'autres manières en tâtonnant un peu plus. Je vous conseille de vous entraîner à les refaire, ces exos-là. Il y en a plusieurs du même type, vous trouvez des matrices. Entraînez-vous, vous refaites celui-ci. Je pense que c'est très bien de s'entraîner à voir les choses, voir ce que c'est l'ensemble image, voir ce que c'est le noyau, parce que ça vous fait aller plus vite et vous sentir plus en confiance. Et ça rend moins mystérieux, ces objets, je trouve, de bien comprendre le lien application linéaire matrice. Voilà, j'espère que ça vous a aidé, et laissez-moi des questions si besoin. Bye bye !

Inverse de matrice

RELATED

Recommended videos

Matrices, produits et composition

Noyau et image par la matrice

Techniques Rapides !