All subjects
All subjects
 All subjects
All subjects
Gaz parfait et piston
Dans cette vidéo, Matisse de Studio aborde un exercice sur le gaz parfait et le piston. Il explique que cet exercice est très classique et revient souvent dans les exercices de col ou en devoirs surveillés, donc il est important de le maîtriser.
L'exercice traite d'une quantité de matière N de gaz parfait enfermée dans une enceinte de surface S. Le piston qui ferme l'enceinte est supposé idéal, c'est-à-dire sans frottement avec l'enceinte. Le piston permet les transferts thermiques et lorsque le système atteint l'équilibre thermique avec l'extérieur, le gaz de l'enceinte est en équilibre thermique avec l'extérieur, qui est à une pression et une température constantes P0 et T0.
L'exercice comporte plusieurs états du système. Dans l'état 1, le système est au repos et a atteint l'équilibre thermique et mécanique. Ensuite, le gaz est chauffé à une température T supérieure à T0, ce qui constitue l'état 2. Une masse supplémentaire M est brusquement placée sur le piston, avant tout transfert thermique, ce qui correspond à l'état 3. Lorsque l'équilibre thermique est atteint, le système est dans l'état 4.
L'objectif de l'exercice est de déterminer les positions H1 à H4 du piston dans chaque état du système, c'est-à-dire la hauteur à laquelle se situe le piston dans chaque situation. Pour cela, Matisse propose de transformer cette notion de hauteur en une autre inconnue plus manipulable, à savoir le volume Vx de l'enceinte renfermée sous le piston. Comme la surface S de l'enceinte est constante, cela permet de déterminer plus facilement les différentes positions.
Pour déterminer le volume V1 dans l'état 1, Matisse établit l'équation d'état des gaz parfaits et montre que V1 est égal à NRT0 divisé par P1S plus Mg. Il explique qu'il faut déterminer P1, qui n'est pas directement donné dans l'énoncé, en utilisant le fait que le piston est à l'équilibre mécanique. Ainsi, il peut établir que P1 est égal à P0 plus Mg divisé par S.
Dans l'état 2, où le gaz est chauffé à une température supérieure, Matisse utilise le raisonnement précédent en changeant simplement la température, ce qui lui permet de déterminer que H2 est égal à nRT divisé par P0S plus Mg.
Dans l'état 3, où une masse supplémentaire est ajoutée brusquement sur le piston, Matisse explique qu'il n'y a pas d'impact sur les variables d'état du système thermique, mais que le bilan des forces appliquées sur le piston doit être ajusté en prenant en compte cette masse supplémentaire. Il conclut que la hauteur H3 est égale à H2.
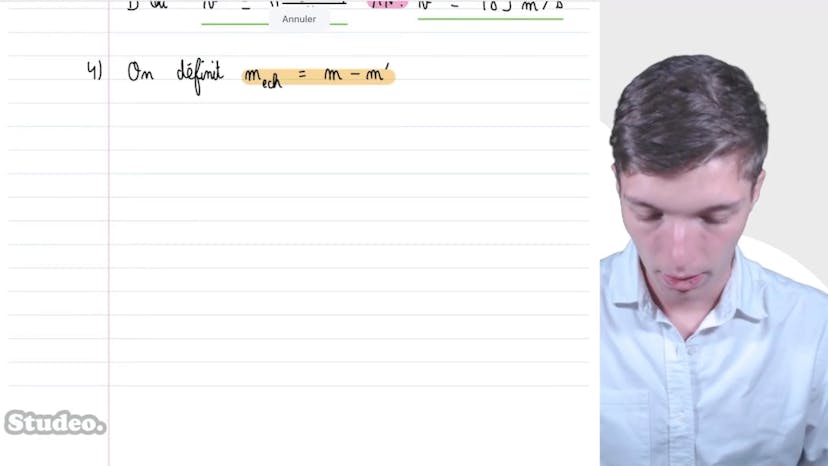
Enfin, dans l'état 4 où l'équilibre thermique est atteint, Matisse montre que la situation est similaire à l'état 2, mais avec la température T0 et la masse effective de petit M plus grand M. Il obtient ainsi que H4 est égal à nRT0 divisé par P0S plus petit M plus grand M fois g.
Matisse souligne l'importance de comprendre la démarche globale de l'exercice et de repérer où chaque variation du système va changer une partie du raisonnement. Il encourage également à justifier chaque étape du raisonnement.
En conclusion, Matisse espère que son explication de cet exercice classique sur le gaz parfait et le piston a été claire et remercie les spectateurs de l'avoir suivi.